Decimal numbers
Definition
When we write numbers, the place of each digit is very important. Look at the number:\(235=\)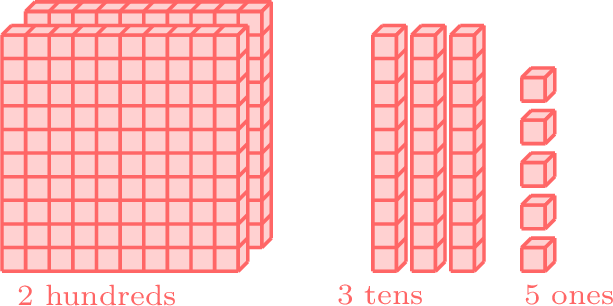
 by 10, we get a tenth which is written as \(\dfrac{1}{10}\) or
by 10, we get a tenth which is written as \(\dfrac{1}{10}\) or  To show where the Ones place is, we use a decimal point:
To show where the Ones place is, we use a decimal point:\(35.4\) = 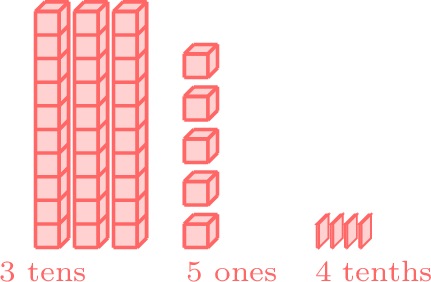

- The 5 is in the Ones place. That means we have 5 ones:
\(5\text{ ones }= 5 =\) 
- The 3 is in the Tens place. That means we have 3 tens:
\(3\text{ tens}=3\times 10=\) 
- The 2 is in the Hundreds place. That means we have 2 hundreds:
\(2\text{ hundreds}=2\times 100=\) 
- 10 ones makes 1 ten:
 = \(10\times 1\) one = 1 ten =
= \(10\times 1\) one = 1 ten = 
- 10 tens make 1 hundred:
 =\(10\times 1\) ten= 1 hundred =
=\(10\times 1\) ten= 1 hundred = 
- 1 hundred \(\div 10=\) 1 ten
- 1 ten \(\div 10=\) 1 one

Definition Decimal Number
A decimal number is a number that has a decimal point. The decimal point separates the whole number part from the part that is smaller than one. We can write a decimal number in different ways:
- Numeral form:
35.48 - Decimal Fraction:
\(\dfrac{3548}{100}\) - Expanded form : $$\begin{aligned}[t] 3\text{ tens }&+& 5\text{ ones }&+& 4\text{ tenths }\\30&+&5&+&\dfrac{4}{10}\\3\times 10&+&5\times 1&+&4\times \dfrac{1}{10}\end{aligned}$$
- Table:
Tens Ones . Tenths Hundredths 3 5 . 4 8 - Blocks:
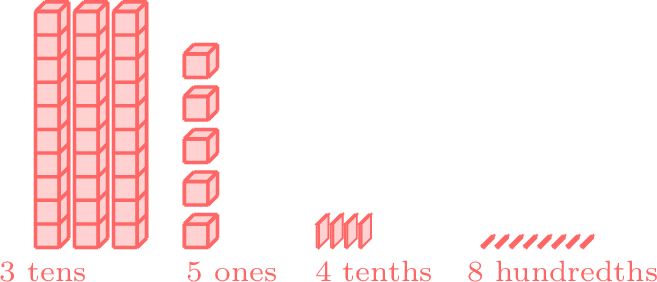
On the Number Line
Decimal numbers, like fractions, can be shown on a number line. A number line helps us see where the numbers go.
- Showing Tenths on a Number Line
- Imagine we cut the space between 0 and 1 into 10 equal parts. Each part is called one tenth, or \(\frac{1}{10}\).

- Since \(\frac{1}{10} = 0.1\), we can write the number line like this:

- Imagine we cut the space between 0 and 1 into 10 equal parts. Each part is called one tenth, or \(\frac{1}{10}\).
- Showing Hundredths on a Number Line
Now, let's zoom in and cut the line between 0 and 0.1 into 10 equal parts. Each tiny part is called one hundredth, or 0.01.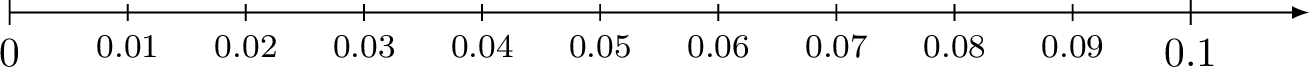
Method How to Draw a Number Line for a Decimal Number
Here's how to put a decimal number on a number line: 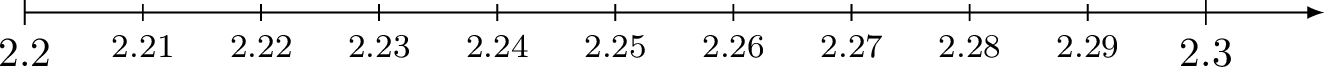
- Choose your range: If your numbers are between 2.2 and 2.3, your number line starts at 2.2 and ends at 2.3.
- Divide into ten equal parts: On a number line from 2.2 to 2.3, the first mark is 2.21, the second is 2.22, and so on, until you get to 2.30 (which is the same as 2.3).
Example
Find the value of \(x\). 
- Each small division on the number line shows 0.01.
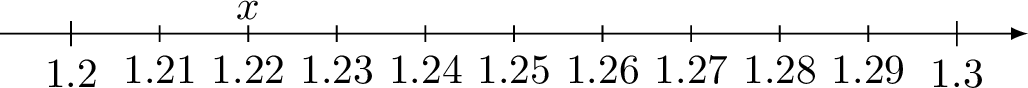
- So, \(x=1.22\)
Ordering
Method Comparing by decimal alignment
- Align the decimal points between the two numbers and add zeros if necessary.
- Compare the digits from left to right. The first number to have a larger digit in any place value is the larger number.
Example
Compare 6.22 and 6.3
- Align the decimal points and add zeros:
6.22
6.30 - Compare from left to right: Both numbers have a 6 in the units place. Comparing the next digit (2 vs. 3) shows that \(6.22\lt 6.3\)
-
 \(\lt\)
\(\lt\)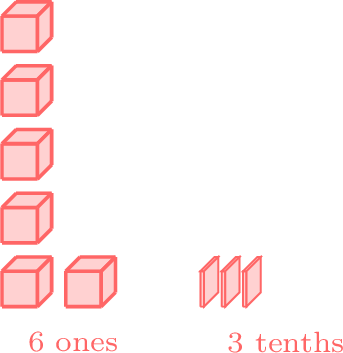
Rounding
Method Rounding Numbers to a Place Value
- Find the digit in the place you are rounding to.
- Look at the digit to the right of it.
- If this digit is 5 or more, add 1 to the digit in the place you are rounding to (round up).
- If this digit is 4 or less, keep the digit the same (round down).
- Replace all digits to the right with zeros.
Example
Round the number \(12.346\) to the nearest tenth.
- Find the digit in the tenths place: \(12.\textcolor{colordef}{3}46\).
- Look at the digit to the right: \(12.\textcolor{colordef}{3}\textcolor{colorprop}{4}6\).
- Since \(\textcolor{colorprop}{4}\) is less than \(5\), keep the digit in the tenths place the same.
- Replace all digits to the right with zeros: \(12.\textcolor{colordef}{3}0\).
Multiplying by Powers of 10
When we multiply a number by 10, each digit shifts one place to the left, making the number ten times larger.$$\begin{aligned}[t]10\times 2.3 &= 10\times (2 \text{ ones} + 3 \text{ tenths})\\&= 2\times 10 \text{ ones} + 3\times \text{10 tenths} \\&= 2 \text{ tens} + 3\text{ ones} \\&= 23\\\end{aligned}$$
Method Multiplying by powers of 10
- When multiplying by 10, we move the decimal point one place to the right.
- When multiplying by 100, we move the decimal point two places to the right.
- When multiplying by 1000, we move the decimal point three places to the right.
Example
Calculate \(10\times 5.24 \)
Dividing by Powers of 10
When we divide a number by 10, each digit shifts one place to the right, making the number ten times smaller.$$\begin{aligned}[t]23\div 10&= (2 \text{ tens } + 3 \text{ ones})\div 10 \\&= \left(2\times \text{tens}\div 10 \right) + \left(3\times \text{ones}\div 10\right)\\&= 2\times \text{ones} + 3\times \text{tenths}\\&= 2.3\\\end{aligned}$$
Method Dividing by powers of 10
- When dividing by 10, we move the decimal point one place to the left.
- When dividing by 100, we move the decimal point two places to the left.
- When dividing by 1000, we move the decimal point three places to the left.
Example
Calculate \(23.2\div 10\)