Multiplication

Multiplication is a very important concept in mathematics. It’s a way of adding the same number together many times.

A) Definitions

Louis loves apples and eats exactly 2 apples every day. He never misses a day because he knows how healthy and tasty apples are.

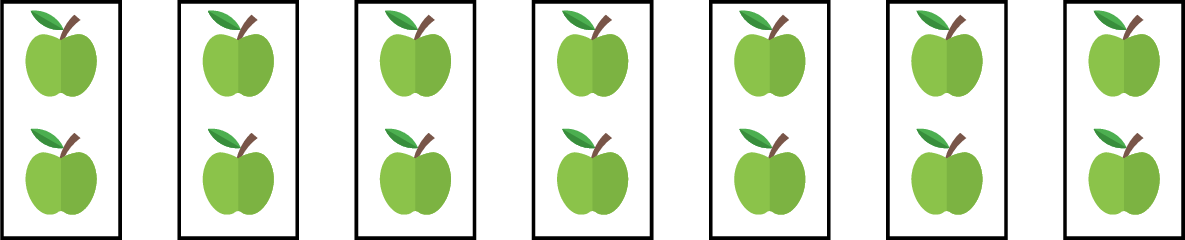
If Louis eats 2 apples every day, how many apples will he eat in one week (7 days)?

Answer

If we want to know how many apples Louis eats in a week (7 days), we add 2 apples for each day:

2 + 2 + 2 + 2 + 2 + 2 + 2

We find

14

apples. In this chapter, we will introduce multiplication to make it quicker and easier. When we say

7

groups of

2

apples, we can write it as

7 \times 2

. The symbol

\times

means multiplied by or times.

7 \times 2 = 2 + 2 + 2 + 2 + 2 + 2 + 2

Definition Multiplication

Multiplication is the process of repeated addition. When we multiply, we calculate the total by adding a number to itself a specified number of times.
Multiplication can be represented in several ways:

Numbers: $4 \times 3 = 12$
Groups: $4 groups of 3 = 12$
Repeated addition: $3 + 3 + 3 + 3 = 12$
Words:four times three equals twelve
Items:
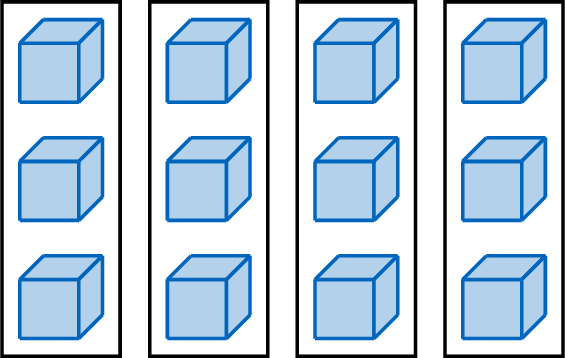
Part-whole model:

Example

Write the repeated addition

5 + 5 + 5

as a multiplication.

Answer

5 + 5 + 5 = 3 \times 5

B) In Number Line

Discover

Let's consider the multiplication:

4 \times 3

that is

3 + 3 + 3 + 3

We can visualize this on a number line:

Starting from 0, we move 3 ones to the right 4 times. Each move represents addition:

0 + 3

3 + 3

6 + 3

9 + 3

. As you can see, we end up at

12

, which is the result of the multiplication

4 \times 3

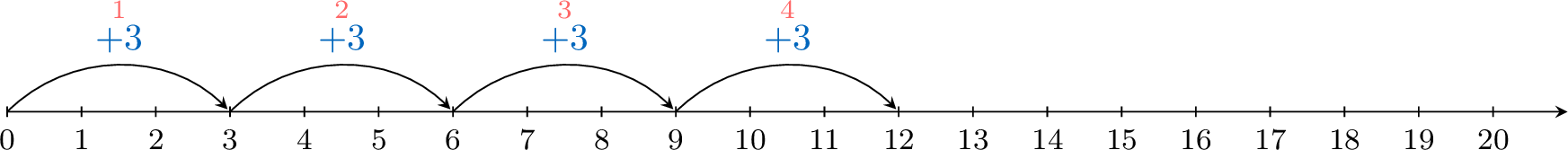
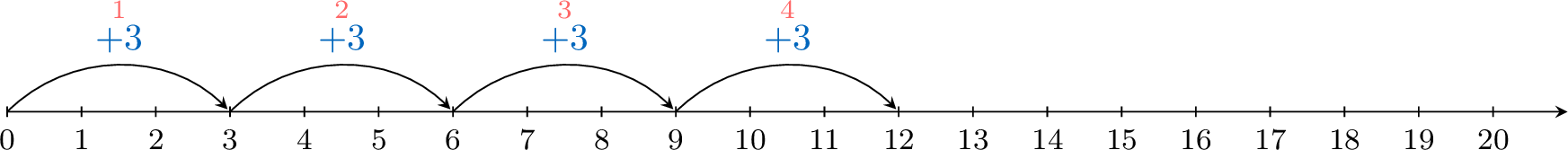
Method Multiplication in number line

To evaluate

4 \times 3

, we start from 0 and we move

3

ones to the right

4

times.

We end up at

12

, which is the result of the multiplication

4 \times 3

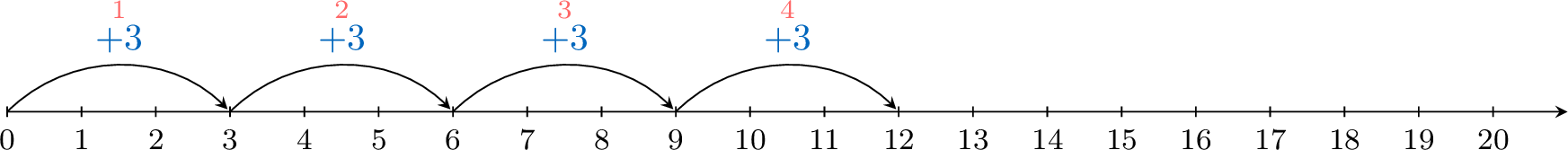
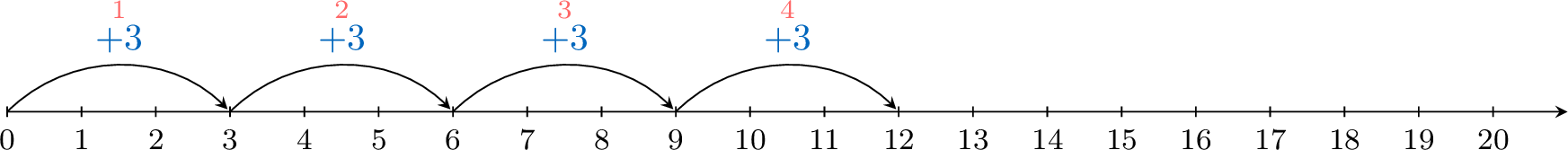
C) Representation of Multiplication in Word Problems

Method Groups of items

When we multiply, we often think about groups and the number of items in each group.

\begin{aligned} number of groups & \times number of items in each group & = & total \end{aligned}

For example, there are

3

bags, and each bag contains

2

apples. The total number of apples is:

\begin{aligned} 3 \times 2 & = 2 + 2 + 2 \\ = 6 \end{aligned}

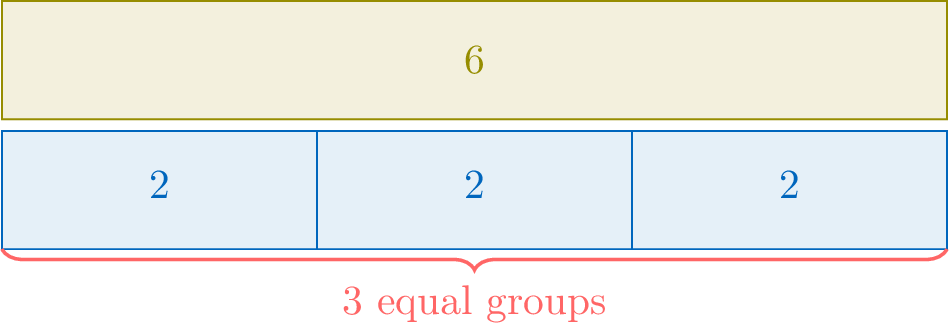
D) Commutative

Discover

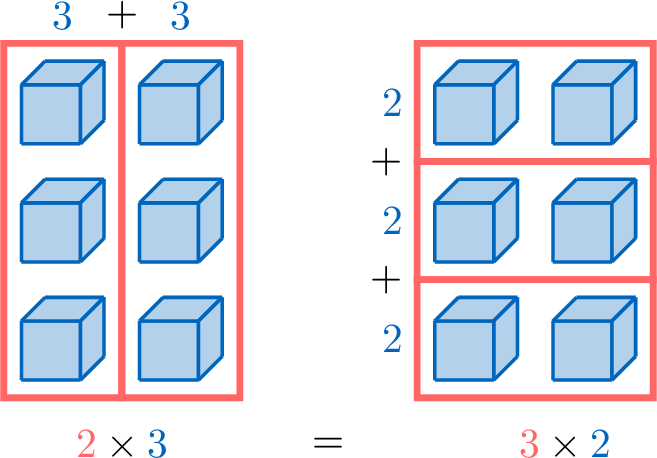
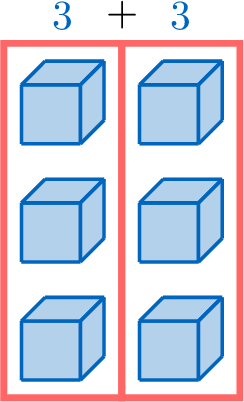
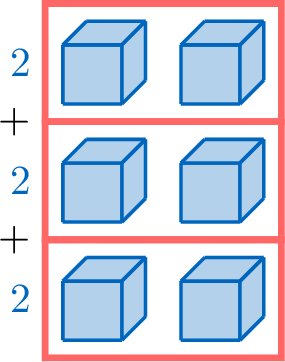
Two brothers, Hugo and Louis, want to count the number of cubes:

Louis calculates $2 \times 3$ to find the number of cubes.
Hugo calculates $3 \times 2$ to find the number of cubes.

Who is correct?

Only Hugo
Only Louis
Both Hugo and Louis

Answer

Both are correct:

Louis counts $2$ groups of $3$ :So, the total is $2 \times 3$ cubes.
Hugo counts $3$ groups of $2$ :So, the total is $3 \times 2$ cubes.

This shows that

2 \times 3 = 3 \times 2

Proposition Commutative