Division
Division is an essential concept in mathematics. It's a way to split a number into equal parts.
Definitions
Kevin, Aisha, and Louis have 6 apples. They want to share these apples equally.

To divide \(\textcolor{olive}{6}\) apples among \(\textcolor{colordef}{3}\) friends:
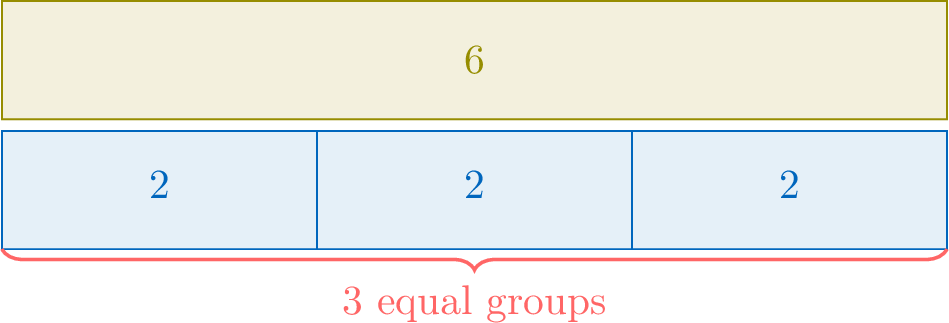
When we say \(\textcolor{olive}{6}\) apples divided among \(\textcolor{colordef}{3}\) friends, we can write it as \(\textcolor{olive}{6}\div \textcolor{colordef}{3}=\textcolor{colorprop}{2}\). The symbol \(\div\) means "divided by."

When we say \(\textcolor{olive}{6}\) apples divided among \(\textcolor{colordef}{3}\) friends, we can write it as \(\textcolor{olive}{6}\div \textcolor{colordef}{3}=\textcolor{colorprop}{2}\). The symbol \(\div\) means "divided by."
Definition Division
Division is the process of splitting a number into equal parts or groups. The \(\div\) symbol indicates division.Division can be represented in several ways:
- Numbers: $$\textcolor{olive}{6}\div \textcolor{colordef}{3}=\textcolor{colorprop}{2}$$
- Words:
six divided by three equals two - Items:
- Part-whole model:
Representations of Division
Method Number of items in each group
When you know the \(\textcolor{olive}{\text{total}}\) and the \(\textcolor{colordef}{\text{number of groups}}\), division finds the \(\textcolor{colorprop}{\text{number of items in each group}}\).$$\begin{aligned}[t]\textcolor{olive}{\text{total}} \div \textcolor{colordef}{\text{number of groups}} &= \textcolor{colorprop}{\text{number of items in each group}}\end{aligned}$$For example, we have \(\textcolor{olive}{12}\) apples, equally shared among \(\textcolor{colordef}{4}\) friends.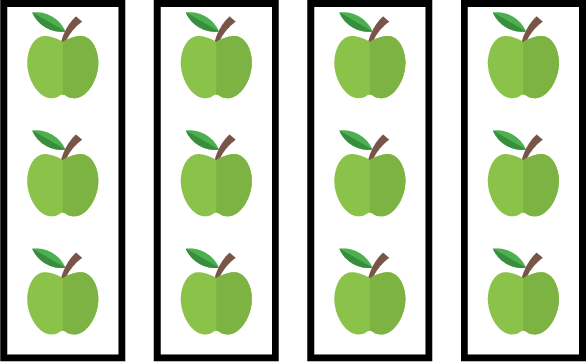



Method Number of groups
If you know the \(\textcolor{olive}{\text{total}}\) and the \(\textcolor{colorprop}{\text{number of items in each group}}\), division finds the \(\textcolor{colordef}{\text{number of groups}}\).$$\begin{aligned}[t]\textcolor{olive}{\text{total}} \div \textcolor{colorprop}{\text{number of items in each group}} &= \textcolor{colordef}{\text{number of groups}}\end{aligned}$$For example, we have \(\textcolor{olive}{15}\) apples and pack them into boxes, each holding \(\textcolor{colorprop}{5}\) apples.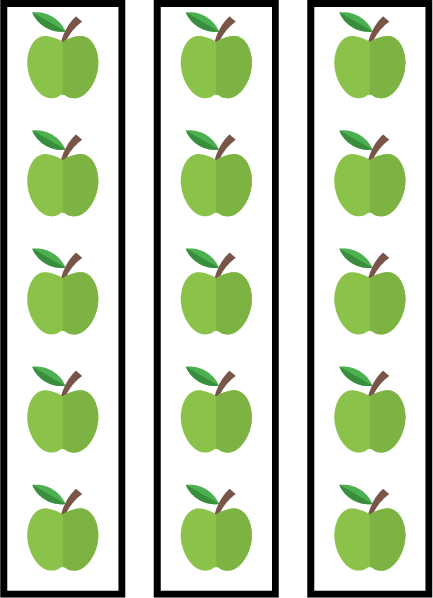

Inverse Operations: Multiplication and Division
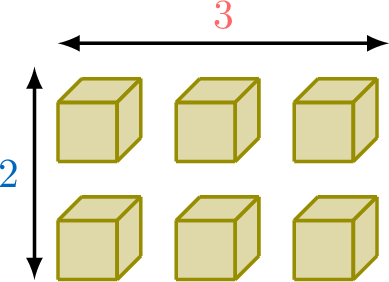
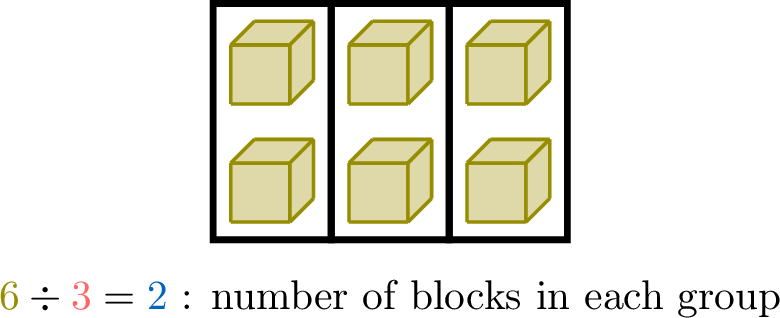
- You have \(\textcolor{colordef}{3}\) columns of \(\textcolor{colorprop}{2}\) cubes each. How many cubes are there in total? (This involves multiplication.)
- You have \(\textcolor{olive}{6}\) cubes to share equally into \(\textcolor{colordef}{3}\) columns. How many cubes will each column have? (This involves division.)
- Total cubes: \(\textcolor{colordef}{3} \times \textcolor{colorprop}{2} = \textcolor{olive}{6}\)
- Each column has \(\textcolor{olive}{6} \div \textcolor{colordef}{3} = \textcolor{colorprop}{2}\) cubes.
Proposition Multiplication and Division are Inverse Operations
Multiplication and division undo each other:$$\begin{aligned}[t]\textcolor{colordef}{3} \times \textcolor{colorprop}{2} &= \textcolor{olive}{6} \\\textcolor{olive}{6} \div \textcolor{colordef}{3} &= \textcolor{colorprop}{2} \\\textcolor{olive}{6} \div \textcolor{colorprop}{2} &= \textcolor{colordef}{3}\end{aligned}$$
