Times Tables

A Tool for Fast Multiplication

There are 5 empty boxes, and each box needs 9 pencils to be full.

Hugo wants to find the total number of pencils needed. How can we help him figure this out?

Hugo could use repeated addition: $$9+9+9+9+9$$But this can be slow. A much faster way is to use multiplication:$$5 \times 9$$If we know our times tables, we know the answer instantly! Because we know that $\textcolor{colordef}{5}\times \textcolor{colorprop}{9}=\textcolor{olive}{45}$, Hugo needs 45 pencils. This is why learning the times tables is so useful—they are a shortcut for solving problems quickly!

Definition Times Table

A times table is a helpful chart that shows the results of multiplying a number by other numbers (usually from 0 to 10). Each number has its own times table.

Example

Use the times table for 4 to calculate $4\times 9$.$$\begin{aligned}\textcolor{colordef}{4}\times \textcolor{colorprop}{0}&=\textcolor{olive}{0}\\ \textcolor{colordef}{4}\times \textcolor{colorprop}{1}&=\textcolor{olive}{4}\\ \textcolor{colordef}{4}\times \textcolor{colorprop}{2}&=\textcolor{olive}{8 }\\ \textcolor{colordef}{4}\times \textcolor{colorprop}{3}&=\textcolor{olive}{12 }\\ \textcolor{colordef}{4}\times \textcolor{colorprop}{4}&=\textcolor{olive}{16 }\\ \textcolor{colordef}{4}\times \textcolor{colorprop}{5}&=\textcolor{olive}{20 }\\ \textcolor{colordef}{4}\times \textcolor{colorprop}{6}&=\textcolor{olive}{24 }\\ \textcolor{colordef}{4}\times \textcolor{colorprop}{7}&=\textcolor{olive}{28 }\\ \textcolor{colordef}{4}\times \textcolor{colorprop}{8}&=\textcolor{olive}{32 }\\ \textcolor{colordef}{4}\times \textcolor{colorprop}{9}&=\textcolor{olive}{36 }\\ \textcolor{colordef}{4}\times \textcolor{colorprop}{10}&=\textcolor{olive}{40}\end{aligned}$$

Answer

Looking at the times table for 4, we can find the line for $4\times 9$ and see that the answer is 36.

Reviewing Our First Times Tables

Proposition Tables of 2, 3, 4, 5, and 10

$\begin{aligned} \textcolor{colordef}{2}\times \textcolor{colorprop}{0}&=\textcolor{olive}{0}\\\textcolor{colordef}{2}\times \textcolor{colorprop}{1}&=\textcolor{olive}{2}\\ \textcolor{colordef}{2}\times \textcolor{colorprop}{2}&=\textcolor{olive}{4 }\\ \textcolor{colordef}{2}\times \textcolor{colorprop}{3}&=\textcolor{olive}{6 }\\ \textcolor{colordef}{2}\times \textcolor{colorprop}{4}&=\textcolor{olive}{8 }\\ \textcolor{colordef}{2}\times \textcolor{colorprop}{5}&=\textcolor{olive}{10 }\\ \textcolor{colordef}{2}\times \textcolor{colorprop}{6}&=\textcolor{olive}{12 }\\ \textcolor{colordef}{2}\times \textcolor{colorprop}{7}&=\textcolor{olive}{14 }\\ \textcolor{colordef}{2}\times \textcolor{colorprop}{8}&=\textcolor{olive}{16 }\\ \textcolor{colordef}{2}\times \textcolor{colorprop}{9}&=\textcolor{olive}{18 }\\ \textcolor{colordef}{2}\times \textcolor{colorprop}{10}&=\textcolor{olive}{20}\end{aligned}$ $\quad \quad$ $\begin{aligned}\textcolor{colordef}{3}\times \textcolor{colorprop}{0}&=\textcolor{olive}{0}\\\textcolor{colordef}{3}\times \textcolor{colorprop}{1}&=\textcolor{olive}{3}\\\textcolor{colordef}{3}\times \textcolor{colorprop}{2}&=\textcolor{olive}{6 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{3}&=\textcolor{olive}{9 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{4}&=\textcolor{olive}{12 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{5}&=\textcolor{olive}{15 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{6}&=\textcolor{olive}{18 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{7}&=\textcolor{olive}{21 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{8}&=\textcolor{olive}{24 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{9}&=\textcolor{olive}{27 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{10}&=\textcolor{olive}{30}\end{aligned}$ $\quad \quad$ $\begin{aligned}\textcolor{colordef}{4}\times \textcolor{colorprop}{0}&=\textcolor{olive}{0}\\\textcolor{colordef}{4}\times \textcolor{colorprop}{1}&=\textcolor{olive}{4}\\\textcolor{colordef}{4}\times \textcolor{colorprop}{2}&=\textcolor{olive}{8 }\\\textcolor{colordef}{4}\times \textcolor{colorprop}{3}&=\textcolor{olive}{12 }\\\textcolor{colordef}{4}\times \textcolor{colorprop}{4}&=\textcolor{olive}{16 }\\\textcolor{colordef}{4}\times \textcolor{colorprop}{5}&=\textcolor{olive}{20 }\\\textcolor{colordef}{4}\times \textcolor{colorprop}{6}&=\textcolor{olive}{24 }\\\textcolor{colordef}{4}\times \textcolor{colorprop}{7}&=\textcolor{olive}{28 }\\\textcolor{colordef}{4}\times \textcolor{colorprop}{8}&=\textcolor{olive}{32 }\\\textcolor{colordef}{4}\times \textcolor{colorprop}{9}&=\textcolor{olive}{36 }\\\textcolor{colordef}{4}\times \textcolor{colorprop}{10}&=\textcolor{olive}{40}\end{aligned}$ $\quad \quad$ $\begin{aligned}\textcolor{colordef}{5}\times \textcolor{colorprop}{0}&=\textcolor{olive}{0}\\\textcolor{colordef}{5}\times \textcolor{colorprop}{1}&=\textcolor{olive}{5}\\\textcolor{colordef}{5}\times \textcolor{colorprop}{2}&=\textcolor{olive}{10 }\\\textcolor{colordef}{5}\times \textcolor{colorprop}{3}&=\textcolor{olive}{15 }\\\textcolor{colordef}{5}\times \textcolor{colorprop}{4}&=\textcolor{olive}{20 }\\\textcolor{colordef}{5}\times \textcolor{colorprop}{5}&=\textcolor{olive}{25 }\\\textcolor{colordef}{5}\times \textcolor{colorprop}{6}&=\textcolor{olive}{30 }\\\textcolor{colordef}{5}\times \textcolor{colorprop}{7}&=\textcolor{olive}{35 }\\\textcolor{colordef}{5}\times \textcolor{colorprop}{8}&=\textcolor{olive}{40 }\\\textcolor{colordef}{5}\times \textcolor{colorprop}{9}&=\textcolor{olive}{45 }\\\textcolor{colordef}{5}\times \textcolor{colorprop}{10}&=\textcolor{olive}{50}\end{aligned}$ $\quad \quad$ $\begin{aligned}\textcolor{colordef}{10} \times \textcolor{colorprop}{0} &= \textcolor{olive}{0} \\\textcolor{colordef}{10} \times \textcolor{colorprop}{1} &= \textcolor{olive}{10} \\\textcolor{colordef}{10} \times \textcolor{colorprop}{2} &= \textcolor{olive}{20} \\\textcolor{colordef}{10} \times \textcolor{colorprop}{3} &= \textcolor{olive}{30} \\\textcolor{colordef}{10} \times \textcolor{colorprop}{4} &= \textcolor{olive}{40} \\\textcolor{colordef}{10} \times \textcolor{colorprop}{5} &= \textcolor{olive}{50} \\\textcolor{colordef}{10} \times \textcolor{colorprop}{6} &= \textcolor{olive}{60} \\\textcolor{colordef}{10} \times \textcolor{colorprop}{7} &= \textcolor{olive}{70} \\\textcolor{colordef}{10} \times \textcolor{colorprop}{8} &= \textcolor{olive}{80} \\\textcolor{colordef}{10} \times \textcolor{colorprop}{9} &= \textcolor{olive}{90} \\\textcolor{colordef}{10} \times \textcolor{colorprop}{10} &= \textcolor{olive}{100}\end{aligned}$

The 6s Times Table

Discover

How many dots are there in total on these 4 dominoes?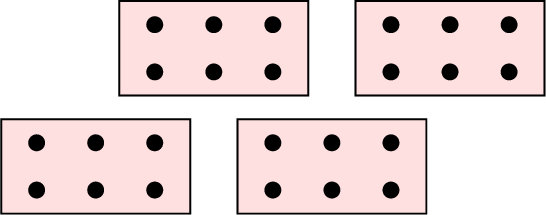

Answer

We have 4 groups of 6. We can skip-count by 6s: 6, 12, 18, 24.

There are $4 \times 6 = 6 + 6 + 6 + 6 = 24$ dots.

Proposition Times Table of 6

$\begin{aligned}\textcolor{colordef}{6}\times \textcolor{colorprop}{0}&=\textcolor{olive}{0}\\\textcolor{colordef}{6}\times \textcolor{colorprop}{1}&=\textcolor{olive}{6}\\\textcolor{colordef}{6}\times \textcolor{colorprop}{2}&=\textcolor{olive}{12 }\\\textcolor{colordef}{6}\times \textcolor{colorprop}{3}&=\textcolor{olive}{18 }\\\textcolor{colordef}{6}\times \textcolor{colorprop}{4}&=\textcolor{olive}{24 }\\\textcolor{colordef}{6}\times \textcolor{colorprop}{5}&=\textcolor{olive}{30 }\\\textcolor{colordef}{6}\times \textcolor{colorprop}{6}&=\textcolor{olive}{36 }\\\textcolor{colordef}{6}\times \textcolor{colorprop}{7}&=\textcolor{olive}{42 }\\\textcolor{colordef}{6}\times \textcolor{colorprop}{8}&=\textcolor{olive}{48 }\\\textcolor{colordef}{6}\times \textcolor{colorprop}{9}&=\textcolor{olive}{54 }\\\textcolor{colordef}{6}\times \textcolor{colorprop}{10}&=\textcolor{olive}{60}\end{aligned}$ $\quad \quad$ $\begin{aligned}\textcolor{colordef}{0}\times \textcolor{colorprop}{6}&=\textcolor{olive}{0}\\\textcolor{colordef}{1}\times \textcolor{colorprop}{6}&=\textcolor{olive}{6}\\\textcolor{colordef}{2}\times \textcolor{colorprop}{6}&=\textcolor{olive}{12}\\\textcolor{colordef}{3}\times \textcolor{colorprop}{6}&=\textcolor{olive}{18}\\\textcolor{colordef}{4}\times \textcolor{colorprop}{6}&=\textcolor{olive}{24}\\\textcolor{colordef}{5}\times \textcolor{colorprop}{6}&=\textcolor{olive}{30}\\\textcolor{colordef}{6}\times \textcolor{colorprop}{6}&=\textcolor{olive}{36}\\\textcolor{colordef}{7}\times \textcolor{colorprop}{6}&=\textcolor{olive}{42}\\\textcolor{colordef}{8}\times \textcolor{colorprop}{6}&=\textcolor{olive}{48}\\\textcolor{colordef}{9}\times \textcolor{colorprop}{6}&=\textcolor{olive}{54}\\\textcolor{colordef}{10}\times \textcolor{colorprop}{6}&=\textcolor{olive}{60}\end{aligned}$

The 7s Times Table

Discover

There are 7 days in a week. How many days are there in 4 weeks?

Answer

We have 4 groups of 7. We can skip-count by 7s: 7, 14, 21, 28 days.

There are $4 \times 7 = 7 + 7 + 7 + 7 = 28$ days.

Proposition Times Table of 7

$\begin{aligned}\textcolor{colordef}{7}\times \textcolor{colorprop}{0}&=\textcolor{olive}{0}\\\textcolor{colordef}{7}\times \textcolor{colorprop}{1}&=\textcolor{olive}{7}\\\textcolor{colordef}{7}\times \textcolor{colorprop}{2}&=\textcolor{olive}{14 }\\\textcolor{colordef}{7}\times \textcolor{colorprop}{3}&=\textcolor{olive}{21 }\\\textcolor{colordef}{7}\times \textcolor{colorprop}{4}&=\textcolor{olive}{28 }\\\textcolor{colordef}{7}\times \textcolor{colorprop}{5}&=\textcolor{olive}{35 }\\\textcolor{colordef}{7}\times \textcolor{colorprop}{6}&=\textcolor{olive}{42 }\\\textcolor{colordef}{7}\times \textcolor{colorprop}{7}&=\textcolor{olive}{49 }\\\textcolor{colordef}{7}\times \textcolor{colorprop}{8}&=\textcolor{olive}{56 }\\\textcolor{colordef}{7}\times \textcolor{colorprop}{9}&=\textcolor{olive}{63 }\\\textcolor{colordef}{7}\times \textcolor{colorprop}{10}&=\textcolor{olive}{70}\end{aligned}$ $\quad \quad$ $\begin{aligned}\textcolor{colordef}{0}\times \textcolor{colorprop}{7}&=\textcolor{olive}{0}\\\textcolor{colordef}{1}\times \textcolor{colorprop}{7}&=\textcolor{olive}{7}\\\textcolor{colordef}{2}\times \textcolor{colorprop}{7}&=\textcolor{olive}{14}\\\textcolor{colordef}{3}\times \textcolor{colorprop}{7}&=\textcolor{olive}{21}\\\textcolor{colordef}{4}\times \textcolor{colorprop}{7}&=\textcolor{olive}{28}\\\textcolor{colordef}{5}\times \textcolor{colorprop}{7}&=\textcolor{olive}{35}\\\textcolor{colordef}{6}\times \textcolor{colorprop}{7}&=\textcolor{olive}{42}\\\textcolor{colordef}{7}\times \textcolor{colorprop}{7}&=\textcolor{olive}{49}\\\textcolor{colordef}{8}\times \textcolor{colorprop}{7}&=\textcolor{olive}{56}\\\textcolor{colordef}{9}\times \textcolor{colorprop}{7}&=\textcolor{olive}{63}\\\textcolor{colordef}{10}\times \textcolor{colorprop}{7}&=\textcolor{olive}{70}\end{aligned}$

The 8s Times Table

Discover

A spider has 8 legs. How many legs do 4 spiders have altogether?

Answer

We have 4 groups of 8. We can skip-count by 8s: 8, 16, 24, 32 legs.

There are $4 \times 8 = 8 + 8 + 8 + 8 = 32$ legs.

Proposition Times Table of 8

$\begin{aligned}\textcolor{colordef}{8}\times \textcolor{colorprop}{0}&=\textcolor{olive}{0}\\\textcolor{colordef}{8}\times \textcolor{colorprop}{1}&=\textcolor{olive}{8}\\\textcolor{colordef}{8}\times \textcolor{colorprop}{2}&=\textcolor{olive}{16 }\\\textcolor{colordef}{8}\times \textcolor{colorprop}{3}&=\textcolor{olive}{24 }\\\textcolor{colordef}{8}\times \textcolor{colorprop}{4}&=\textcolor{olive}{32 }\\\textcolor{colordef}{8}\times \textcolor{colorprop}{5}&=\textcolor{olive}{40 }\\\textcolor{colordef}{8}\times \textcolor{colorprop}{6}&=\textcolor{olive}{48 }\\\textcolor{colordef}{8}\times \textcolor{colorprop}{7}&=\textcolor{olive}{56 }\\\textcolor{colordef}{8}\times \textcolor{colorprop}{8}&=\textcolor{olive}{64 }\\\textcolor{colordef}{8}\times \textcolor{colorprop}{9}&=\textcolor{olive}{72 }\\\textcolor{colordef}{8}\times \textcolor{colorprop}{10}&=\textcolor{olive}{80}\end{aligned}$ $\quad \quad$ $\begin{aligned}\textcolor{colordef}{0}\times \textcolor{colorprop}{8}&=\textcolor{olive}{0}\\\textcolor{colordef}{1}\times \textcolor{colorprop}{8}&=\textcolor{olive}{8}\\\textcolor{colordef}{2}\times \textcolor{colorprop}{8}&=\textcolor{olive}{16}\\\textcolor{colordef}{3}\times \textcolor{colorprop}{8}&=\textcolor{olive}{24}\\\textcolor{colordef}{4}\times \textcolor{colorprop}{8}&=\textcolor{olive}{32}\\\textcolor{colordef}{5}\times \textcolor{colorprop}{8}&=\textcolor{olive}{40}\\\textcolor{colordef}{6}\times \textcolor{colorprop}{8}&=\textcolor{olive}{48}\\\textcolor{colordef}{7}\times \textcolor{colorprop}{8}&=\textcolor{olive}{56}\\\textcolor{colordef}{8}\times \textcolor{colorprop}{8}&=\textcolor{olive}{64}\\\textcolor{colordef}{9}\times \textcolor{colorprop}{8}&=\textcolor{olive}{72}\\\textcolor{colordef}{10}\times \textcolor{colorprop}{8}&=\textcolor{olive}{80}\end{aligned}$

The 9s Times Table

Discover

There are 9 players on a baseball team. How many players are in 5 teams?

Answer

We have 5 groups of 9. We can skip-count by 9s: 9, 18, 27, 36, 45 players.

There are $5 \times 9 = 9 + 9 + 9 + 9 + 9 = 45$ players.

Proposition Times Table of 9

$\begin{aligned}\textcolor{colordef}{9}\times \textcolor{colorprop}{0}&=\textcolor{olive}{0}\\\textcolor{colordef}{9}\times \textcolor{colorprop}{1}&=\textcolor{olive}{9}\\\textcolor{colordef}{9}\times \textcolor{colorprop}{2}&=\textcolor{olive}{18 }\\\textcolor{colordef}{9}\times \textcolor{colorprop}{3}&=\textcolor{olive}{27 }\\\textcolor{colordef}{9}\times \textcolor{colorprop}{4}&=\textcolor{olive}{36 }\\\textcolor{colordef}{9}\times \textcolor{colorprop}{5}&=\textcolor{olive}{45 }\\\textcolor{colordef}{9}\times \textcolor{colorprop}{6}&=\textcolor{olive}{54 }\\\textcolor{colordef}{9}\times \textcolor{colorprop}{7}&=\textcolor{olive}{63 }\\\textcolor{colordef}{9}\times \textcolor{colorprop}{8}&=\textcolor{olive}{72 }\\\textcolor{colordef}{9}\times \textcolor{colorprop}{9}&=\textcolor{olive}{81 }\\\textcolor{colordef}{9}\times \textcolor{colorprop}{10}&=\textcolor{olive}{90}\end{aligned}$ $\quad \quad$ $\begin{aligned}\textcolor{colordef}{0}\times \textcolor{colorprop}{9}&=\textcolor{olive}{0}\\\textcolor{colordef}{1}\times \textcolor{colorprop}{9}&=\textcolor{olive}{9}\\\textcolor{colordef}{2}\times \textcolor{colorprop}{9}&=\textcolor{olive}{18}\\\textcolor{colordef}{3}\times \textcolor{colorprop}{9}&=\textcolor{olive}{27}\\\textcolor{colordef}{4}\times \textcolor{colorprop}{9}&=\textcolor{olive}{36}\\\textcolor{colordef}{5}\times \textcolor{colorprop}{9}&=\textcolor{olive}{45}\\\textcolor{colordef}{6}\times \textcolor{colorprop}{9}&=\textcolor{olive}{54}\\\textcolor{colordef}{7}\times \textcolor{colorprop}{9}&=\textcolor{olive}{63}\\\textcolor{colordef}{8}\times \textcolor{colorprop}{9}&=\textcolor{olive}{72}\\\textcolor{colordef}{9}\times \textcolor{colorprop}{9}&=\textcolor{olive}{81}\\\textcolor{colordef}{10}\times \textcolor{colorprop}{9}&=\textcolor{olive}{90}\end{aligned}$

The Full Multiplication Grid

Proposition All Times Tables from 1 to 10

This grid is a powerful tool that shows all the times tables from 1 to 10 in one place. To find the answer to a problem like $7 \times 8$, find the row for 7 and the column for 8, and see where they meet!

$\times$	$\textcolor{colorprop}{1}$	$\textcolor{colorprop}{2}$	$\textcolor{colorprop}{3}$	$\textcolor{colorprop}{4}$	$\textcolor{colorprop}{5}$	$\textcolor{colorprop}{6}$	$\textcolor{colorprop}{7}$	$\textcolor{colorprop}{8}$	$\textcolor{colorprop}{9}$	$\textcolor{colorprop}{10}$
$\textcolor{colordef}{1}$	$\textcolor{olive}{1}$	$\textcolor{olive}{2}$	$\textcolor{olive}{3}$	$\textcolor{olive}{4}$	$\textcolor{olive}{5}$	$\textcolor{olive}{6}$	$\textcolor{olive}{7}$	$\textcolor{olive}{8}$	$\textcolor{olive}{9}$	$\textcolor{olive}{10}$
$\textcolor{colordef}{2}$	$\textcolor{olive}{2}$	$\textcolor{olive}{4}$	$\textcolor{olive}{6}$	$\textcolor{olive}{8}$	$\textcolor{olive}{10}$	$\textcolor{olive}{12}$	$\textcolor{olive}{14}$	$\textcolor{olive}{16}$	$\textcolor{olive}{18}$	$\textcolor{olive}{20}$
$\textcolor{colordef}{3}$	$\textcolor{olive}{3}$	$\textcolor{olive}{6}$	$\textcolor{olive}{9}$	$\textcolor{olive}{12}$	$\textcolor{olive}{15}$	$\textcolor{olive}{18}$	$\textcolor{olive}{21}$	$\textcolor{olive}{24}$	$\textcolor{olive}{27}$	$\textcolor{olive}{30}$
$\textcolor{colordef}{4}$	$\textcolor{olive}{4}$	$\textcolor{olive}{8}$	$\textcolor{olive}{12}$	$\textcolor{olive}{16}$	$\textcolor{olive}{20}$	$\textcolor{olive}{24}$	$\textcolor{olive}{28}$	$\textcolor{olive}{32}$	$\textcolor{olive}{36}$	$\textcolor{olive}{40}$
$\textcolor{colordef}{5}$	$\textcolor{olive}{5}$	$\textcolor{olive}{10}$	$\textcolor{olive}{15}$	$\textcolor{olive}{20}$	$\textcolor{olive}{25}$	$\textcolor{olive}{30}$	$\textcolor{olive}{35}$	$\textcolor{olive}{40}$	$\textcolor{olive}{45}$	$\textcolor{olive}{50}$
$\textcolor{colordef}{6}$	$\textcolor{olive}{6}$	$\textcolor{olive}{12}$	$\textcolor{olive}{18}$	$\textcolor{olive}{24}$	$\textcolor{olive}{30}$	$\textcolor{olive}{36}$	$\textcolor{olive}{42}$	$\textcolor{olive}{48}$	$\textcolor{olive}{54}$	$\textcolor{olive}{60}$
$\textcolor{colordef}{7}$	$\textcolor{olive}{7}$	$\textcolor{olive}{14}$	$\textcolor{olive}{21}$	$\textcolor{olive}{28}$	$\textcolor{olive}{35}$	$\textcolor{olive}{42}$	$\textcolor{olive}{49}$	$\textcolor{olive}{56}$	$\textcolor{olive}{63}$	$\textcolor{olive}{70}$
$\textcolor{colordef}{8}$	$\textcolor{olive}{8}$	$\textcolor{olive}{16}$	$\textcolor{olive}{24}$	$\textcolor{olive}{32}$	$\textcolor{olive}{40}$	$\textcolor{olive}{48}$	$\textcolor{olive}{56}$	$\textcolor{olive}{64}$	$\textcolor{olive}{72}$	$\textcolor{olive}{80}$
$\textcolor{colordef}{9}$	$\textcolor{olive}{9}$	$\textcolor{olive}{18}$	$\textcolor{olive}{27}$	$\textcolor{olive}{36}$	$\textcolor{olive}{45}$	$\textcolor{olive}{54}$	$\textcolor{olive}{63}$	$\textcolor{olive}{72}$	$\textcolor{olive}{81}$	$\textcolor{olive}{90}$
$\textcolor{colordef}{10}$	$\textcolor{olive}{10}$	$\textcolor{olive}{20}$	$\textcolor{olive}{30}$	$\textcolor{olive}{40}$	$\textcolor{olive}{50}$	$\textcolor{olive}{60}$	$\textcolor{olive}{70}$	$\textcolor{olive}{80}$	$\textcolor{olive}{90}$	$\textcolor{olive}{100}$

\(\times\)	\(\textcolor{colorprop}{1}\)	\(\textcolor{colorprop}{2}\)	\(\textcolor{colorprop}{3}\)	\(\textcolor{colorprop}{4}\)	\(\textcolor{colorprop}{5}\)	\(\textcolor{colorprop}{6}\)	\(\textcolor{colorprop}{7}\)	\(\textcolor{colorprop}{8}\)	\(\textcolor{colorprop}{9}\)	\(\textcolor{colorprop}{10}\)
\(\textcolor{colordef}{1}\)	\(\textcolor{olive}{1}\)	\(\textcolor{olive}{2}\)	\(\textcolor{olive}{3}\)	\(\textcolor{olive}{4}\)	\(\textcolor{olive}{5}\)	\(\textcolor{olive}{6}\)	\(\textcolor{olive}{7}\)	\(\textcolor{olive}{8}\)	\(\textcolor{olive}{9}\)	\(\textcolor{olive}{10}\)
\(\textcolor{colordef}{2}\)	\(\textcolor{olive}{2}\)	\(\textcolor{olive}{4}\)	\(\textcolor{olive}{6}\)	\(\textcolor{olive}{8}\)	\(\textcolor{olive}{10}\)	\(\textcolor{olive}{12}\)	\(\textcolor{olive}{14}\)	\(\textcolor{olive}{16}\)	\(\textcolor{olive}{18}\)	\(\textcolor{olive}{20}\)
\(\textcolor{colordef}{3}\)	\(\textcolor{olive}{3}\)	\(\textcolor{olive}{6}\)	\(\textcolor{olive}{9}\)	\(\textcolor{olive}{12}\)	\(\textcolor{olive}{15}\)	\(\textcolor{olive}{18}\)	\(\textcolor{olive}{21}\)	\(\textcolor{olive}{24}\)	\(\textcolor{olive}{27}\)	\(\textcolor{olive}{30}\)
\(\textcolor{colordef}{4}\)	\(\textcolor{olive}{4}\)	\(\textcolor{olive}{8}\)	\(\textcolor{olive}{12}\)	\(\textcolor{olive}{16}\)	\(\textcolor{olive}{20}\)	\(\textcolor{olive}{24}\)	\(\textcolor{olive}{28}\)	\(\textcolor{olive}{32}\)	\(\textcolor{olive}{36}\)	\(\textcolor{olive}{40}\)
\(\textcolor{colordef}{5}\)	\(\textcolor{olive}{5}\)	\(\textcolor{olive}{10}\)	\(\textcolor{olive}{15}\)	\(\textcolor{olive}{20}\)	\(\textcolor{olive}{25}\)	\(\textcolor{olive}{30}\)	\(\textcolor{olive}{35}\)	\(\textcolor{olive}{40}\)	\(\textcolor{olive}{45}\)	\(\textcolor{olive}{50}\)
\(\textcolor{colordef}{6}\)	\(\textcolor{olive}{6}\)	\(\textcolor{olive}{12}\)	\(\textcolor{olive}{18}\)	\(\textcolor{olive}{24}\)	\(\textcolor{olive}{30}\)	\(\textcolor{olive}{36}\)	\(\textcolor{olive}{42}\)	\(\textcolor{olive}{48}\)	\(\textcolor{olive}{54}\)	\(\textcolor{olive}{60}\)
\(\textcolor{colordef}{7}\)	\(\textcolor{olive}{7}\)	\(\textcolor{olive}{14}\)	\(\textcolor{olive}{21}\)	\(\textcolor{olive}{28}\)	\(\textcolor{olive}{35}\)	\(\textcolor{olive}{42}\)	\(\textcolor{olive}{49}\)	\(\textcolor{olive}{56}\)	\(\textcolor{olive}{63}\)	\(\textcolor{olive}{70}\)
\(\textcolor{colordef}{8}\)	\(\textcolor{olive}{8}\)	\(\textcolor{olive}{16}\)	\(\textcolor{olive}{24}\)	\(\textcolor{olive}{32}\)	\(\textcolor{olive}{40}\)	\(\textcolor{olive}{48}\)	\(\textcolor{olive}{56}\)	\(\textcolor{olive}{64}\)	\(\textcolor{olive}{72}\)	\(\textcolor{olive}{80}\)
\(\textcolor{colordef}{9}\)	\(\textcolor{olive}{9}\)	\(\textcolor{olive}{18}\)	\(\textcolor{olive}{27}\)	\(\textcolor{olive}{36}\)	\(\textcolor{olive}{45}\)	\(\textcolor{olive}{54}\)	\(\textcolor{olive}{63}\)	\(\textcolor{olive}{72}\)	\(\textcolor{olive}{81}\)	\(\textcolor{olive}{90}\)
\(\textcolor{colordef}{10}\)	\(\textcolor{olive}{10}\)	\(\textcolor{olive}{20}\)	\(\textcolor{olive}{30}\)	\(\textcolor{olive}{40}\)	\(\textcolor{olive}{50}\)	\(\textcolor{olive}{60}\)	\(\textcolor{olive}{70}\)	\(\textcolor{olive}{80}\)	\(\textcolor{olive}{90}\)	\(\textcolor{olive}{100}\)