Scale Diagrams
Definitions
When designing a house, an architect doesn’t draw the house at its actual size. That would be far too big to fit on paper! Instead, the architect draws a smaller version of the house where every measurement is reduced by the same amount, called the scale. For house plans, a scale of \(1{:}100\) is often used, meaning the house is drawn \(100\) times smaller than it really is.\includegraphics[width=0.5\textwidth]{\imagepath floorplan2.png} These smaller versions are called scale diagrams.
Definition Scale Diagram
A scale diagram is a way of representing an object at a different proportion to its real-world size using a scale, which is a ratio expressed as \(1{:}\text{scale factor}\) or \(1/\text{scale factor}\).$$\frac{\textcolor{colorprop}{1}}{\textcolor{colordef}{\text{Scale factor}}}= \frac{\textcolor{colorprop}{\text{Drawn length}}}{\textcolor{colordef}{\text{Actual length}}}$$
Formulae
Proposition Formulae
$$\begin{aligned}\text{Actual length} &= \text{Drawn length} \times \text{Scale factor}\\
\text{Drawn length} &= \text{Actual length} \div \text{Scale factor}\\
\text{Scale factor} &= \frac{\text{Actual length}}{\text{Drawn length}}\end{aligned}$$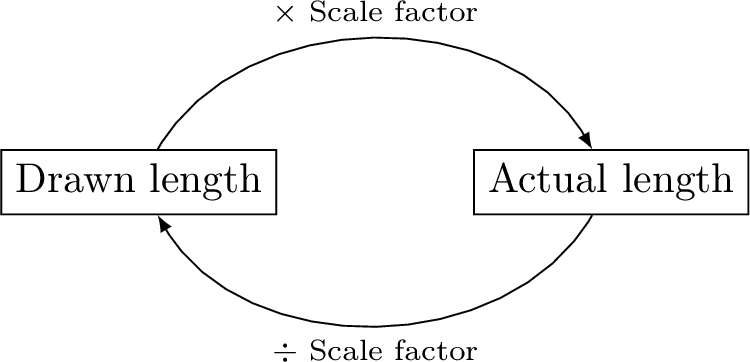

$$\frac{\textcolor{colorprop}{1}}{\textcolor{colordef}{\text{Scale factor}}}= \frac{\textcolor{colorprop}{\text{Drawn length}}}{\textcolor{colordef}{\text{Actual length}}}$$$$\textcolor{colorprop}{1} \times \textcolor{colordef}{\text{Actual length}} = \textcolor{colorprop}{\text{Drawn length}} \times \textcolor{colordef}{\text{Scale factor}}\hspace{1em} \text{(cross multiplication)}$$$$\textcolor{colordef}{\text{Actual length}} = \textcolor{colorprop}{\text{Drawn length}} \times \textcolor{colordef}{\text{Scale factor}}\hspace{1em} \text{(simplification)}$$
Example
Find the width of this house: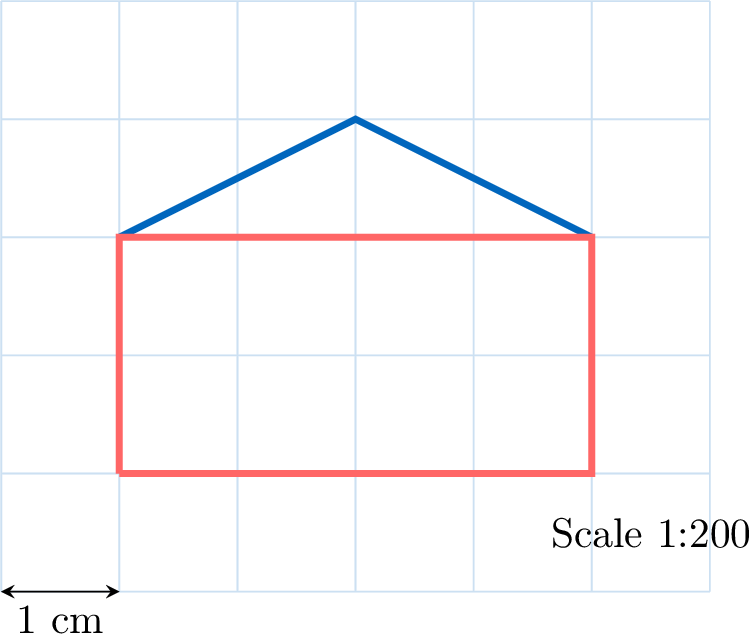

The drawn width of the house is \(4\,\mathrm{cm}\).$$\begin{aligned}\text{Actual width} &= \text{Drawn width} \times \text{Scale factor}\\
&= 4\,\mathrm{cm} \times 200 \\
&= 800\,\mathrm{cm} \\
&= 8\,\mathrm{m}\end{aligned}$$The actual width of the house is \(8\) meters.
Example
For the scale \(1{:}200\), find the drawn length corresponding to an actual length of \(6\,\mathrm{m}\).
$$\begin{aligned}\text{Drawn length} &= \frac{\text{Actual length}}{\text{Scale factor}}\\
&= \frac{6\,\mathrm{m}}{200}\\
&= \frac{600\,\mathrm{cm}}{200} &&(\text{unit conversion})\\
&= 3\,\mathrm{cm}\end{aligned}$$So, \(6\,\mathrm{m}\) of actual length represents \(3\,\mathrm{cm}\) of drawn length.
Example
\(2\,\mathrm{cm}\) of drawn length represents \(5\,\mathrm{m}\) of actual length.
Find the scale factor.
Find the scale factor.
$$\begin{aligned}\text{Scale factor} &= \frac{\text{Actual length}}{\text{Drawn length}}\\
&= \frac{5\,\mathrm{m}}{2\,\mathrm{cm}}\\
&= \frac{500\,\mathrm{cm}}{2\,\mathrm{cm}} &&(\text{converting to the same units})\\
&= 250\end{aligned}$$So, the scale factor is \(250\).