Percentages
Definition
Definition Percentage
A percentage is a ratio out of \(100\).
\(\pourcent\) is read ``percent'', meaning ``out of a hundred.''
\(\pourcent\) is read ``percent'', meaning ``out of a hundred.''
Example

Percentage as a Number
By definition, the percentage \(\textcolor{colorprop}{5}\textcolor{colordef}{\pourcent}\) is equal to the fraction \(\dfrac{\textcolor{colorprop}{5}}{\textcolor{colordef}{100}}\). Also, the fraction \(\dfrac{\textcolor{colorprop}{5}}{\textcolor{colordef}{100}}\) is equal to the decimal number \(0.05\), since \(5\div 100=0.05\). It is important to be able to convert between these different representations of a percentage.
Method Converting a Percentage to a Fraction
To convert the percentage \(\textcolor{colorprop}{5}\textcolor{colordef}{\pourcent}\) into a fraction, use the definition:$$\textcolor{colorprop}{5}\textcolor{colordef}{\pourcent} = \dfrac{\textcolor{colorprop}{5}}{\textcolor{colordef}{100}}$$
Method Converting a Fraction to a Percentage
To convert the fraction \(\dfrac{\textcolor{colorprop}{3}}{\textcolor{colordef}{4}}\) into a percentage:
- Method 1 (Equivalent Fractions)
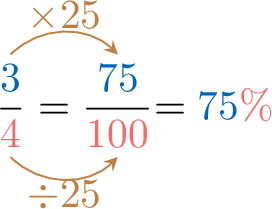
- Method 2 (Formula)$$\begin{aligned}\dfrac{\textcolor{colorprop}{3}}{\textcolor{colordef}{4}} &= \left( \dfrac{\textcolor{colorprop}{3}}{\textcolor{colordef}{4}} \times \textcolor{colordef}{100} \right)\textcolor{colordef}{\pourcent} \\ &= \textcolor{colorprop}{75}\textcolor{colordef}{\pourcent} \quad \text{(compute } 3 \div 4 \times 100 = 75)\end{aligned}$$
Method Converting a Percentage to a Decimal
To convert the percentage \(\textcolor{colorprop}{5}\textcolor{colordef}{\pourcent}\) into a decimal:$$\begin{aligned}\textcolor{colorprop}{5}\textcolor{colordef}{\pourcent} &= \dfrac{\textcolor{colorprop}{5}}{\textcolor{colordef}{100}} \\
&= \textcolor{colorprop}{5} \div \textcolor{colordef}{100} \\
&= 0.05\end{aligned}$$
Method Converting a Decimal to a Percentage
To convert the decimal \(0.05\) into a percentage:$$\begin{aligned}0.05 &= 0.05 \times \textcolor{colordef}{100}\textcolor{colordef}{\pourcent} \\
&= \textcolor{colorprop}{5}\textcolor{colordef}{\pourcent}\end{aligned}$$
Ratio to Percentage
We use percentages to compare a part with a whole.
For example, in a class with \(\textcolor{colordef}{20}\) students, there are \(\textcolor{colorprop}{12}\) girls. To find the percentage of girls in the class, we find an equivalent fraction with a denominator of 100:$$\begin{aligned}\frac{\textcolor{colorprop}{x}}{\textcolor{colordef}{100}} &= \frac{\textcolor{colorprop}{12}}{\textcolor{colordef}{20}}\\ \textcolor{colorprop}{x} &= \frac{\textcolor{colorprop}{12}}{\textcolor{colordef}{20}} \times \textcolor{colordef}{100} && \text{(multiplying both sides by }\textcolor{colordef}{100})\\ \textcolor{colorprop}{x} &= \textcolor{colorprop}{60}\\ \end{aligned}$$The percentage of girls in the class is \(\textcolor{colorprop}{60}\textcolor{colordef}{\pourcent}\). This means \(\textcolor{colorprop}{60}\) out of every \(\textcolor{colordef}{100}\) students are girls.
For example, in a class with \(\textcolor{colordef}{20}\) students, there are \(\textcolor{colorprop}{12}\) girls. To find the percentage of girls in the class, we find an equivalent fraction with a denominator of 100:$$\begin{aligned}\frac{\textcolor{colorprop}{x}}{\textcolor{colordef}{100}} &= \frac{\textcolor{colorprop}{12}}{\textcolor{colordef}{20}}\\ \textcolor{colorprop}{x} &= \frac{\textcolor{colorprop}{12}}{\textcolor{colordef}{20}} \times \textcolor{colordef}{100} && \text{(multiplying both sides by }\textcolor{colordef}{100})\\ \textcolor{colorprop}{x} &= \textcolor{colorprop}{60}\\ \end{aligned}$$The percentage of girls in the class is \(\textcolor{colorprop}{60}\textcolor{colordef}{\pourcent}\). This means \(\textcolor{colorprop}{60}\) out of every \(\textcolor{colordef}{100}\) students are girls.
Method Ratio to Percentage
To calculate the percentage of a ratio of a part to the whole, use the following formula:$$\textcolor{colorprop}{x}\textcolor{colordef}{\pourcent}= \left(\frac{\textcolor{colorprop}{\text{part}}}{\textcolor{colordef}{\text{whole}}} \times \textcolor{colordef}{100}\right)\textcolor{colordef}{\pourcent}$$
Example
You took a math quiz and answered \(\textcolor{colorprop}{21}\) questions correctly out of \(\textcolor{colordef}{24}\) questions total.
Calculate the percentage of correct answers.
Calculate the percentage of correct answers.
- The \(\textcolor{colorprop}{\text{part}}\) is the number of correct answers: \(\textcolor{colorprop}{21}\).
- The \(\textcolor{colordef}{\text{whole}}\) is the total number of questions: \(\textcolor{colordef}{24}\).
- \(\begin{aligned}[t]\text{Percentage of correct answers} &= \left(\frac{\textcolor{colorprop}{\text{part}}}{\textcolor{colordef}{\text{whole}}} \times \textcolor{colordef}{100}\right)\textcolor{colordef}{\pourcent}\\&= \left(\frac{\textcolor{colorprop}{21}}{\textcolor{colordef}{24}} \times \textcolor{colordef}{100}\right)\textcolor{colordef}{\pourcent}\\ &= \textcolor{colorprop}{87.5}\textcolor{colordef}{\pourcent} \quad \text{(compute: } 21 \div 24 \times 100 = 87.5)\end{aligned}\)
Comparing Percentages
In Parliament A of Country A, there are \(\textcolor{colorprop}{26}\) women out of \(\textcolor{colordef}{50}\) deputies. In Parliament B of Country B, there are \(\textcolor{colorprop}{30}\) women out of \(\textcolor{colordef}{80}\) deputies. Hugo says, "Since there are more women in Parliament B, women are better represented in this parliament." Do you agree with that statement?
- \(\begin{aligned}[t]\text{Percentage of women in Parliament A} &= \left(\frac{\textcolor{colorprop}{26}}{\textcolor{colordef}{50}} \times \textcolor{colordef}{100}\right)\textcolor{colordef}{\pourcent} \\&= \textcolor{colorprop}{52}\textcolor{colordef}{\pourcent}\end{aligned}\)
In Parliament A, \(\textcolor{colorprop}{52}\) out of every \(\textcolor{colordef}{100}\) deputies are women. - \(\begin{aligned}[t]\text{Percentage of women in Parliament B} &= \left(\frac{\textcolor{colorprop}{30}}{\textcolor{colordef}{80}} \times \textcolor{colordef}{100}\right)\textcolor{colordef}{\pourcent} \\&= \textcolor{colorprop}{37.5}\textcolor{colordef}{\pourcent}\end{aligned}\)
In Parliament B, \(\textcolor{colorprop}{37.5}\) out of every \(\textcolor{colordef}{100}\) deputies are women.
Method Comparing Percentages
- Step 1: Calculate the percentage for each group.
- Step 2: Compare the percentages and conclude.
Formula to Find a Part Using Percentages
Method Finding a Part Using Percentages
To calculate a part in a part-to-whole relationship, multiply the percentage by the whole:$$\textcolor{colorprop}{\text{part}} = \textcolor{colorprop}{x}\textcolor{colordef}{\pourcent} \times \textcolor{colordef}{\text{whole}}$$
$$\begin{aligned}\frac{\textcolor{colorprop}{\text{part}}}{\textcolor{colordef}{\text{whole}}} &= \textcolor{colorprop}{x}\textcolor{colordef}{\pourcent} \\
\textcolor{colorprop}{\text{part}} &= \textcolor{colorprop}{x}\textcolor{colordef}{\pourcent} \times \textcolor{colordef}{\text{whole}} &&\text{(multiplying both sides by }\textcolor{colordef}{\text{whole}})\end{aligned}$$
Example
In a school with \(\textcolor{colordef}{200}\) students, \(\textcolor{colorprop}{60}\textcolor{colordef}{\pourcent}\) are girls.
Calculate the number of girls in the school.
Calculate the number of girls in the school.
- Method 1 (using the formula)$$\begin{aligned}[t]\textcolor{colorprop}{\text{number of girls}} &= \textcolor{colorprop}{60}\textcolor{colordef}{\pourcent} \text{ of } \textcolor{colordef}{200\text{ students}} \\ &= \textcolor{colorprop}{60}\textcolor{colordef}{\pourcent} \times \textcolor{colordef}{200} \\ &= \frac{\textcolor{colorprop}{60}}{\textcolor{colordef}{100}} \times \textcolor{colordef}{200} \\ &= \textcolor{colorprop}{120} & \text{(compute: } (60 \div 100) \times 200 = 120)\end{aligned}$$
- Method 2 (cross-multiplication)$$\begin{aligned}\frac{\textcolor{colorprop}{60}}{\textcolor{colordef}{100}} &= \frac{\textcolor{colorprop}{\text{number of girls}}}{\textcolor{colordef}{200}} \\ \textcolor{colordef}{100} \times \textcolor{colorprop}{\text{number of girls}} &= \textcolor{colorprop}{60} \times \textcolor{colordef}{200} &&\text{(cross-multiplication)} \\ \textcolor{colorprop}{\text{number of girls}} &= \frac{\textcolor{colorprop}{60} \times \textcolor{colordef}{200}}{\textcolor{colordef}{100}} &&\text{(dividing both sides by }\textcolor{colordef}{100}) \\ \textcolor{colorprop}{\text{number of girls}} &= \textcolor{colorprop}{120} &&\text{(compute: } (60 \times 200) \div 100 = 120)\end{aligned}$$
Formula to Find the Whole Using Percentages
Method Finding the Whole Using Percentages
To calculate the whole in a part-to-whole relationship, divide the part by the percentage (as a decimal):$$\textcolor{colordef}{\text{whole}} = \dfrac{\textcolor{colorprop}{\text{part}}}{\textcolor{colorprop}{x}\textcolor{colordef}{\pourcent}}$$
$$\begin{aligned}\frac{\textcolor{colorprop}{\text{part}}}{\textcolor{colordef}{\text{whole}}} &= \textcolor{colorprop}{x}\textcolor{colordef}{\pourcent} \\
\textcolor{colorprop}{\text{part}} &= \textcolor{colorprop}{x}\textcolor{colordef}{\pourcent} \times \textcolor{colordef}{\text{whole}} \\
\textcolor{colordef}{\text{whole}} &= \dfrac{\textcolor{colorprop}{\text{part}}}{\textcolor{colorprop}{x}\textcolor{colordef}{\pourcent}} &&\text{(dividing both sides by }\textcolor{colorprop}{x}\textcolor{colordef}{\pourcent})\end{aligned}$$
Example
In a class, \(\textcolor{colorprop}{40}\textcolor{colordef}{\pourcent}\) of the students are girls, and there are \(\textcolor{colorprop}{14}\) girls in total.
Find the total number of students in the class.
Find the total number of students in the class.
- Method 1 (using the formula)$$\begin{aligned}\textcolor{colordef}{\text{total students}} &= \dfrac{\textcolor{colorprop}{14}}{\textcolor{colorprop}{40}\textcolor{colordef}{\pourcent}} \\ &= \dfrac{\textcolor{colorprop}{14}}{\left( \dfrac{\textcolor{colorprop}{40}}{\textcolor{colordef}{100}} \right)} \\ &= \textcolor{colordef}{35} &&\text{(compute: } 14 \div (40 \div 100) = 35)\end{aligned}$$
- Method 2 (cross-multiplication)$$\begin{aligned}\frac{\textcolor{colorprop}{40}}{\textcolor{colordef}{100}} &= \frac{\textcolor{colorprop}{14}}{\textcolor{colordef}{\text{total students}}} \\ \textcolor{colorprop}{40} \times \textcolor{colordef}{\text{total students}} &= \textcolor{colordef}{100} \times \textcolor{colorprop}{14} &&\text{(cross-multiplication)} \\ \textcolor{colordef}{\text{total students}} &= \frac{\textcolor{colordef}{100} \times \textcolor{colorprop}{14}}{\textcolor{colorprop}{40}} &&\text{(dividing both sides by }\textcolor{colorprop}{40}) \\ \textcolor{colordef}{\text{total students}} &= \textcolor{colordef}{35} &&\text{(compute: } (100 \times 14) \div 40 = 35)\end{aligned}$$
Percentage Increase or Decrease
In everyday life, there are many situations where quantities are either increased or decreased by a certain percentage. For example:
- A store offers a 20\(\pourcent\) discount on all items during a sale.
- A worker receives a salary increase of 7\(\pourcent\).
- A person on a diet reduces their weight by 10\(\pourcent\).
Definition Percentage Increase or Decrease
- A percentage increase occurs when a quantity is raised by a certain percentage.
- A percentage decrease occurs when a quantity is reduced by a certain percentage.
Method Calculating the New Quantity for a Percentage Increase in Two Steps
- Calculate the increase: $$ \begin{aligned} \text{Increase} &= \text{Percentage of the original quantity} \\ &= \text{Percentage} \times \text{Original quantity} \end{aligned} $$
- Calculate the new quantity: $$ \text{New quantity} = \text{Original quantity} + \text{Increase} $$
Example
If the original price of a shirt is \dollar 50 and it is increased by 20\(\pourcent\), find the new price.
- Calculate the increase: $$ \begin{aligned} \text{Increase} &= 20\pourcent \times \dollar 50 \\ &= \frac{20}{100} \times \dollar 50 \\ &= \dollar 10 \end{aligned} $$
- Calculate the new price: $$ \text{New price} = \dollar 50 + \dollar 10 = \dollar 60 $$
Method Calculating the New Quantity for a Percentage Decrease in Two Steps
- Calculate the decrease: $$ \begin{aligned} \text{Decrease} &= \text{Percentage of the original quantity} \\ &= \text{Percentage} \times \text{Original quantity} \end{aligned} $$
- Calculate the new quantity: $$ \text{New quantity} = \text{Original quantity} - \text{Decrease} $$
Example
If the original price of a shirt is \(\dollar\)50 and it is decreased by 20\(\pourcent\), find the new price.
- Calculate the decrease: $$ \begin{aligned} \text{Decrease} &= 20\pourcent \times \dollar 50 \\ &= \frac{20}{100} \times \dollar 50 \\ &= \dollar 10 \end{aligned} $$
- Calculate the new price: $$ \text{New price} = \dollar 50 - \dollar 10 = \dollar 40 $$
Percentage Change
Percentage Change measures how much a quantity has increased or decreased relative to its original value. It can be expressed as either a percentage increase or a percentage decrease, depending on the nature of the change.
Definition Percentage Change
- If the quantity increases, the percentage change is positive: $$ \textcolor{colordef}{\text{Percentage Change} = \text{Percentage Increase}} $$
- If the quantity decreases, the percentage change is negative: $$ \textcolor{colordef}{\text{Percentage Change} = -\text{Percentage Decrease}} $$
Example
A store offers a discount of \(25\pourcent\). Determine the percentage change.
A discount is a decrease in price, so the percentage change is negative. The discount is \(25\pourcent\), so the percentage change is \(-25\pourcent\).
The relationship between the new quantity and the original quantity can be expressed as:
Proposition Percentage Increase or Decrease in One Step
$$\begin{aligned}\text{New Quantity} &= \text{Original Quantity} + \text{Percentage Change} \times \text{Original Quantity} \\
&= (1 + \text{Percentage Change}) \times \text{Original Quantity}\end{aligned}$$
Definition Multiplier
\((1 + \text{Percentage Change})\) is the multiplier.
Example
Increase \(\dollar200\) by \(10\pourcent\).
It is an increase, so the percentage change is \(10\pourcent\).$$\begin{aligned}\text{New amount} &= \left(1 + \frac{10}{100}\right) \times \dollar200 \\
&= 1.10 \times \dollar200 \\
&= \dollar220\end{aligned}$$
Formula to Find the Percentage Change
Method Calculating the Percentage Change
$$\text{Percentage Change} = \frac{\text{New Quantity} - \text{Original Quantity}}{\text{Original Quantity}} \times 100\pourcent$$Note: The result is expressed as a percentage.
$$\begin{aligned}\text{Original Quantity} + \text{Percentage Change} \times \text{Original Quantity} &= \text{New Quantity} \\
\text{Percentage Change} \times \text{Original Quantity} &= \text{New Quantity} - \text{Original Quantity} \\
\text{Percentage Change} &= \frac{\text{New Quantity} - \text{Original Quantity}}{\text{Original Quantity}} \\
\text{Percentage Change} &= \frac{\text{New Quantity} - \text{Original Quantity}}{\text{Original Quantity}} \times 100\pourcent\end{aligned}$$Note: In the first three steps, the percentage change is in decimal form. Multiplying by \(100\pourcent\) gives the percentage form.
Example
Find the percentage change in Louis's weight from 25 kg to 28 kg.
Since 28 kg is greater than 25 kg, it is an increase.$$\begin{aligned}\text{Percentage Change} &= \frac{28 - 25}{25} \times 100\pourcent \\
&= \frac{3}{25} \times 100\pourcent \\
&= 12\pourcent\end{aligned}$$This is a \(12\pourcent\) increase.