Algebra
Definitions
Definition Constant
A constant is a number.
Example
\(0, \; 3, \; \pi\)
Definition Variable
A variable is a quantity which we represent by a letter.
Example
Definition Expression
An expression is an algebraic form consisting of constants, variables, and operation signs such as \(+,-,\times,\div\) and \(\sqrt{\ }\).
Example
Definition Equation
An equation is a mathematical statement consisting of two expressions, the left-hand side and the right-hand side, separated by an equal sign \(=\).
Example
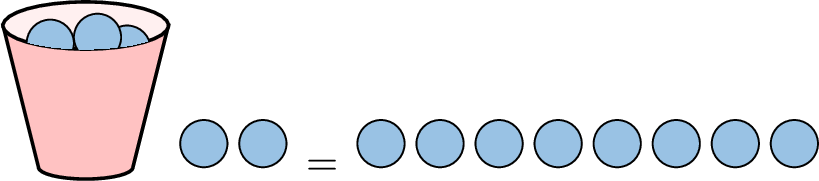
Definition Formula
A formula is an equation, often related to the real world, to physics or to geometry.
Example
For a triangle: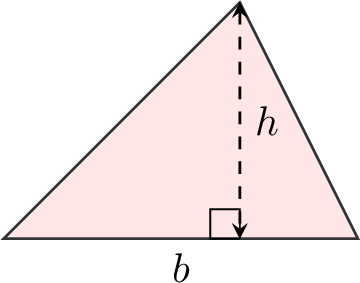 ,\(A = \dfrac{b \times h}{2}\) is the formula for the area.
,\(A = \dfrac{b \times h}{2}\) is the formula for the area.
 ,\(A = \dfrac{b \times h}{2}\) is the formula for the area.
,\(A = \dfrac{b \times h}{2}\) is the formula for the area.
Notations
Definition Product notation
We can omit the \(\times\) sign when it is followed by a variable or a parenthesis.
Example
- \(2 \times x = 2x\)
- \(2 \times (L+l) = 2(L+l)\)
Definition Repeated addition
$$\overbrace{x + x + \ldots + x}^{n\text{ terms}} = n\times x$$
Example
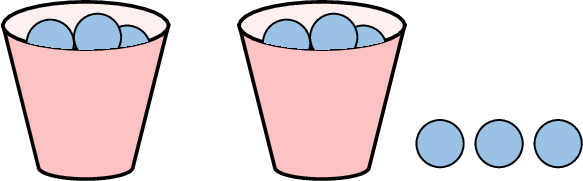
$$x + x + 1+1 +1=2x +3$$
Definition Repeated multiplication
$$\overbrace{x \times x \times \ldots \times x}^{n\text{ factors}} = x^n$$
Example
For a circle: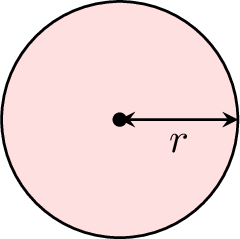 , simplify the formula for the area \(A = \pi \times r \times r\).
, simplify the formula for the area \(A = \pi \times r \times r\).
 , simplify the formula for the area \(A = \pi \times r \times r\).
, simplify the formula for the area \(A = \pi \times r \times r\).
$$\begin{aligned}A &= \pi \times r \times r \\
&= \pi r^2\end{aligned}$$
Identity
Three students were asked to find the formula for the perimeter of the rectangle: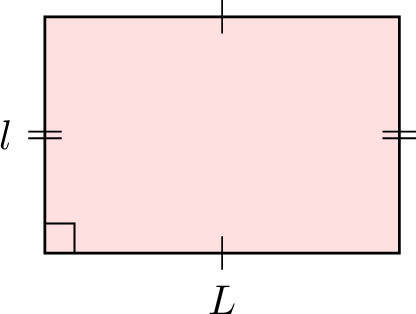

- Su: \(P = 2(l + L)\)
- Louis: \(P = l + L + l + L\)
- Hugo: \(P = 2l + 2L\)
They are all correct. These three expressions \(2(l + L)\), \(l + L + l + L\) and \(2l + 2L\) produce the same result for the perimeter of the rectangle for all values of \(l\) and \(L\). They are called identities.
Definition Identity
An identity is an equality between two expressions such that their evaluations produce the same value for all values of the variables.
Identities are fundamental in algebra: they allow us to transform and simplify expressions and are the foundation for solving equations and manipulating formulas.
Proposition 0 and 1 Identities
$$1 \times x = x \qquad \text{and} \qquad 0 \times x = 0$$
Proposition Commutativity Identities
$$\textcolor{colordef}{a} + \textcolor{colorprop}{b} = \textcolor{colorprop}{b} + \textcolor{colordef}{a}\qquad \text{and} \qquad\textcolor{colordef}{a} \times \textcolor{colorprop}{b} = \textcolor{colorprop}{b} \times \textcolor{colordef}{a}$$
Proposition Associativity Identities
$$(\textcolor{colordef}{a} + \textcolor{colorprop}{b}) + \textcolor{olive}{c} = \textcolor{colordef}{a} + (\textcolor{colorprop}{b} + \textcolor{olive}{c})\qquad \text{and} \qquad(\textcolor{colordef}{a} \times \textcolor{colorprop}{b}) \times \textcolor{olive}{c} = \textcolor{colordef}{a} \times (\textcolor{colorprop}{b} \times \textcolor{olive}{c})$$
Example
Show that \(l + L + l + L = 2l + 2L\).
$$\begin{aligned}\textcolor{colordef}{l} + \textcolor{colorprop}{L} + \textcolor{colordef}{l} + \textcolor{colorprop}{L}&= \textcolor{colordef}{l + l} + \textcolor{colorprop}{L + L} && (\text{collecting terms}) \\
&= \textcolor{colordef}{2l} + \textcolor{colorprop}{2L} && (\text{repeated addition})\end{aligned}$$
Method Simplifying by Collecting Like Terms
Simplifying an expression by collecting like terms involves combining terms that have the same variables raised to the same powers.
- Identify like terms: Like terms are terms that have the same variable(s) raised to the same power. For example, \(3x\) and \(5x\) are like terms, but \(3x\) and \(3x^2\) are not.
- Regroupe like terms: Add or subtract the coefficients (numerical parts) of the like terms. The variable part remains the same.
Example
Simplify the expression: \(2x + 4 + x - 2\)
$$\begin{aligned}[h]2x + 4 + x - 2 &= \textcolor{colordef}{2x} \textcolor{colorprop}{+4} \textcolor{colordef}{+x} \textcolor{colorprop}{-2} &&(\text{identifying like terms}) \\
&= \textcolor{colordef}{(2+1)x} + \textcolor{colorprop}{4-2} &&(\text{combining like terms}) \\
&= \textcolor{colordef}{3x} + \textcolor{colorprop}{2} &&(\text{simplifying})\end{aligned}$$
Substituting
Definition Substituting
Substituting is replacing a variable in an expression or equation with a specific value.
To avoid confusion with signs, especially when substituting negative values, we usually write substitutions in parentheses.
Method Evaluating
To evaluate an expression, substitute a number for each variable and perform the arithmetic operations.
Example
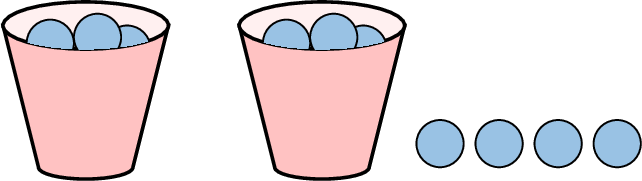
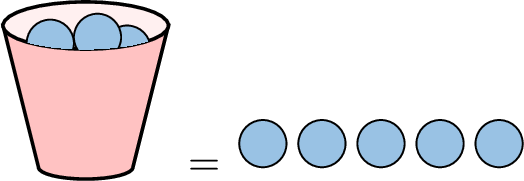
$$\begin{aligned}2x + 4 &= 2 \times \textcolor{olive}{(5)} + 4 \quad (\text{substituting } \textcolor{olive}{x=5}) \\
&= 10 + 4 \\
&= 14\end{aligned}$$There are 14 marbles.