Proportionality
Definition
Imagine you are buying cookies. The price is \(\dollar 2\) per cookie. The number of cookies is \(\textcolor{colordef}{x}\) and the total cost is \(\textcolor{colorprop}{y}\). We have:

| \(\textcolor{colordef}{1}\) cookie costs | \(\textcolor{colorprop}{2} = \textcolor{olive}{2} \times \textcolor{colordef}{1}\) |
| \(\textcolor{colordef}{2}\) cookies cost | \(\textcolor{colorprop}{4} = \textcolor{olive}{2} \times \textcolor{colordef}{2}\) |
| \(\textcolor{colordef}{3}\) cookies cost | \(\textcolor{colorprop}{6} = \textcolor{olive}{2} \times \textcolor{colordef}{3}\) |
| \(\textcolor{colordef}{4}\) cookies cost | \(\textcolor{colorprop}{8} = \textcolor{olive}{2} \times \textcolor{colordef}{4}\) |
| \(\textcolor{colordef}{x}\) cookies cost | \(\textcolor{colorprop}{y} = \textcolor{olive}{2} \times \textcolor{colordef}{x}\) |

- Ratio definition: No matter how many cookies you buy, the ratio \(\dfrac{\textcolor{colorprop}{y}}{\textcolor{colordef}{x}}\) is always the same:$$\dfrac{\textcolor{colorprop}{8}}{\textcolor{colordef}{4}} =\dfrac{\textcolor{colorprop}{6}}{\textcolor{colordef}{3}} = \dfrac{\textcolor{colorprop}{4}}{\textcolor{colordef}{2}} = \dfrac{\textcolor{colorprop}{y}}{\textcolor{colordef}{x}} =\textcolor{olive}{ 2}$$
- Linearity definition: we can also express the total cost as a formula:$$\textcolor{colorprop}{y} = \textcolor{olive}{2} \times \textcolor{colordef}{x}$$
Definition Proportional
Two variables \(\textcolor{colordef}{x}\) and \(\textcolor{colorprop}{y}\) are proportional if the ratio of the two variables is equal to a constant value \(\textcolor{olive}{k}\) called the coefficient of proportionality.$$\dfrac{\textcolor{colorprop}{y}}{\textcolor{colordef}{x}} = \textcolor{olive}{k} $$Alternatively, \(\textcolor{colorprop}{y}\) is proportional to \(\textcolor{colordef}{x}\) if$$ \textcolor{colorprop}{y} = \textcolor{olive}{k}\times \textcolor{colordef}{x}$$
Example
Is this table proportional?
| \(\textcolor{colordef}{x}\) | \(\textcolor{colordef}{1}\) | \(\textcolor{colordef}{2}\) | \(\textcolor{colordef}{3}\) |
| \(\textcolor{colorprop}{y}\) | \(\textcolor{colorprop}{15}\) | \(\textcolor{colorprop}{30}\) | \(\textcolor{colorprop}{45}\) |
Yes. Each ratio is equal: \(\dfrac{\textcolor{colorprop}{15}}{\textcolor{colordef}{1}} = \dfrac{\textcolor{colorprop}{30}}{\textcolor{colordef}{2}} = \dfrac{\textcolor{colorprop}{45}}{\textcolor{colordef}{3}} = \textcolor{olive}{15}\).
Calculating a Fourth Proportional
Method Calculating a Fourth Proportional
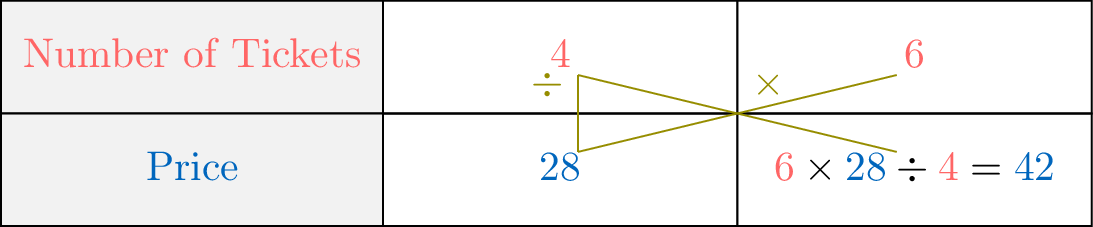
If 4 tickets cost \(\dollar\)28, how much do 6 tickets cost if each ticket costs the same?
- Method 1: Using the Coefficient of Proportionality
Find the unit price (price for 1 ticket):$$\text{Unit price} = \dfrac{28}{4} = 7$$Now multiply by 6 for 6 tickets:$$\text{Total for 6 tickets} = 7 \times 6 = 42$$ - Method 2: Proportion Equation$$\begin{aligned}\dfrac{\textcolor{colorprop}{28}}{\textcolor{colordef}{4}} &= \dfrac{\textcolor{colorprop}{x}}{\textcolor{colordef}{6}} \\ \textcolor{colordef}{4} \times \textcolor{colorprop}{x} &= \textcolor{colorprop}{28} \times \textcolor{colordef}{6} && \text{(cross multiplication)} \\ \textcolor{colorprop}{x} &= \dfrac{\textcolor{colorprop}{28} \times \textcolor{colordef}{6}}{\textcolor{colordef}{4}} \\ \textcolor{colorprop}{x} &= \textcolor{colorprop}{42}\end{aligned}$$
- Method 3: Unit Rate with Equivalent Ratios
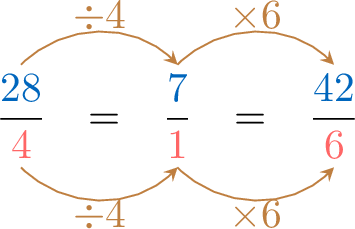
- Method 4: Product in Cross