Square Roots
Definition
- When we square a number, we multiply it by itself.
For example, 3 squared is \(3 \times 3\), which can be written as \(3^2\).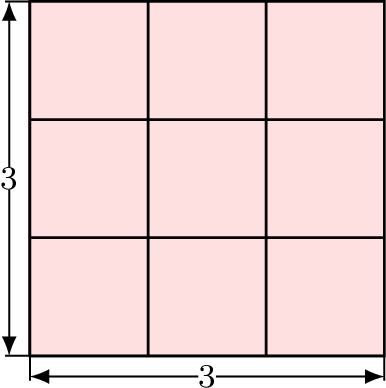
\(3^2=9\) is the area of a square with side length \(3\). - On the other hand, taking the square root of a number is the reverse process: it is finding a number that, when multiplied by itself, gives the original number. For example,
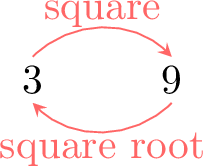
3 squared is 9, so the square root of 9 is 3.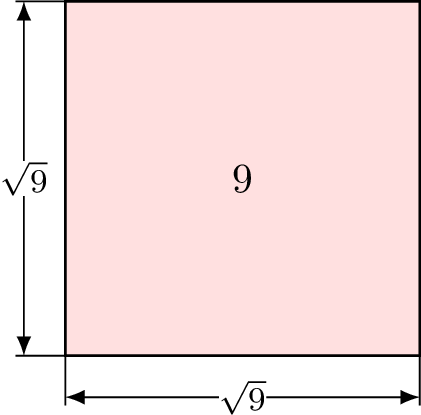
The square root of \(9\), written as \(\sqrt{9}\), is the side length of a square with area 9.
Definition Square root
The square root of \(a\), written \(\sqrt{a}\), is the positive number which, when squared, gives \(a\):$$\left(\sqrt{a}\right)^2 =\sqrt{a} \times \sqrt{a}=a$$
Example
Find \(\sqrt{25}\).
Since \(5 \times 5 = 25\), \(\sqrt{25}=5\).
Definition Perfect Squares
A perfect square is a number that is the result of squaring an integer.
Example
The perfect squares of the first few integers are:
1, 4, 9, 16, 25, 36, 49, 64, and so on.
1, 4, 9, 16, 25, 36, 49, 64, and so on.
Calculating Square Roots
It is easy to calculate the square root of a perfect square, but determining the square root of other numbers can be quite challenging.
Method Use a calculator
- Press the square root button \(\boxed{\sqrt{\;}}\)
- Enter the number
- Press the equals button \(\boxed{=}\)
By entering \(\sqrt{10}\) and pressing the equals button, the calculator displays: \(3.16227766017\).
So \(\sqrt{10} \approx 3.2\).
So \(\sqrt{10} \approx 3.2\).