Solving Equations
Definitions
Welcome to the Math Escape Room! Today, you will embark on a journey to find the secret one-digit code. With your team, you must use your problem-solving skills to crack the code!
The code is:$$\triangle + 10 = 1 + 2 \times 6$$$$\triangle = \boxed{\phantom{\triangle}}$$You have only one opportunity.
The code is:$$\triangle + 10 = 1 + 2 \times 6$$$$\triangle = \boxed{\phantom{\triangle}}$$You have only one opportunity.
- Louis proposes to enter \(\boxed{8}\)
- Su proposes to enter \(\boxed{3}\)
We will test each proposed code to determine which one satisfies the given equation.
- Test Louis's code: \(\textcolor{colordef}{\triangle = 8}\) $$ \begin{aligned} \textcolor{colordef}{(8)} + 10 &= 1 + 2 \times 6 \quad &&\text{(Substitute)} \\ 18 &= 1 + 12 \\ 18 &= 13 \quad &&\text{(False)} \end{aligned} $$
- Test Su's code: \(\textcolor{colordef}{\triangle = 3}\) $$ \begin{aligned} \textcolor{colordef}{(3)} + 10 &= 1 + 2 \times 6 \quad &&\text{(Substitute)} \\ 13 &= 1 + 12 \\ 13 &= 13 \quad &&\text{(True)} \end{aligned} $$
Definition Solving an Equation
Solving an equation involves finding the values of the variable, called solutions, that make the equation true.
In this context, the variable is called the unknown.
We often use the letter \(x\) to represent the unknown.
In this context, the variable is called the unknown.
We often use the letter \(x\) to represent the unknown.
Example
Show that a solution of \(3 + x = 5\) is \(x = 2\).
For \(\textcolor{colordef}{x = 2}\):$$\begin{aligned}3 + \textcolor{colordef}{(2)} &= 5 \quad &&\text{(substituting)} \\
5 &= 5 \quad &&\text{(True)}\end{aligned}$$
Example
Show that \(x = 1\) is not a solution of \(3 + x = 5\).
For \(\textcolor{colordef}{x = 1}\):$$\begin{aligned}3 + \textcolor{colordef}{(1)} &= 5 \quad &&\text{(substituting)} \\
4 &= 5 \quad &&\text{(False)}\end{aligned}$$
Solving by Trial and Error
Method Trial and Error
The trial and error method is a problem-solving strategy used to find a solution to an equation by testing different values for the unknown variable until the correct value is found.
Example
Consider the equation \(2x + 3 = 11\).
Use the trial and error method to find a solution.
Use the trial and error method to find a solution.
- Let's try \(\textcolor{colordef}{x = 2}\): $$ \begin{aligned} 2 \times \textcolor{colordef}{(2)} + 3 &= 11 \quad &&\text{(Substitute)} \\ 4 + 3 &= 11 \\ 7 &= 11 \quad &&\text{(False)} \end{aligned} $$
- Let's try \(\textcolor{colordef}{x = 3}\): $$ \begin{aligned} 2 \times \textcolor{colordef}{(3)} + 3 &= 11 \quad &&\text{(Substitute)} \\ 6 + 3 &= 11 \\ 9 &= 11 \quad &&\text{(False)} \end{aligned} $$
- Let's try \(\textcolor{colordef}{x = 4}\): $$ \begin{aligned} 2 \times \textcolor{colordef}{(4)} + 3 &= 11 \quad &&\text{(Substitute)} \\ 8 + 3 &= 11 \\ 11 &= 11 \quad &&\text{(True)} \end{aligned} $$
Equivalent Equations
Definition Equivalent Equations
Two equations are equivalent if they have the same solutions.
An equation can be visually represented using the concept of a balance scale.
Definition Balance Scale
A balance scale has two pans, and when the weights on both pans are equal, the scale is in balance.
Representation of the equation \(2x + 10 = 80\)

Representation of the equation \(2x + 10 = 80\)
Proposition Operations for Equivalent Equations
Equivalent equations are created by performing the same operation on both sides:
- Adding or subtracting the same number on both sides
Equation Balance scale \(x + 10 = 80 \) 
Subtract 10 from both sides Remove a weight of 10 from both pans \(\begin{aligned}x+10-10 &= 80-10 \\x &= 70\end{aligned}\) 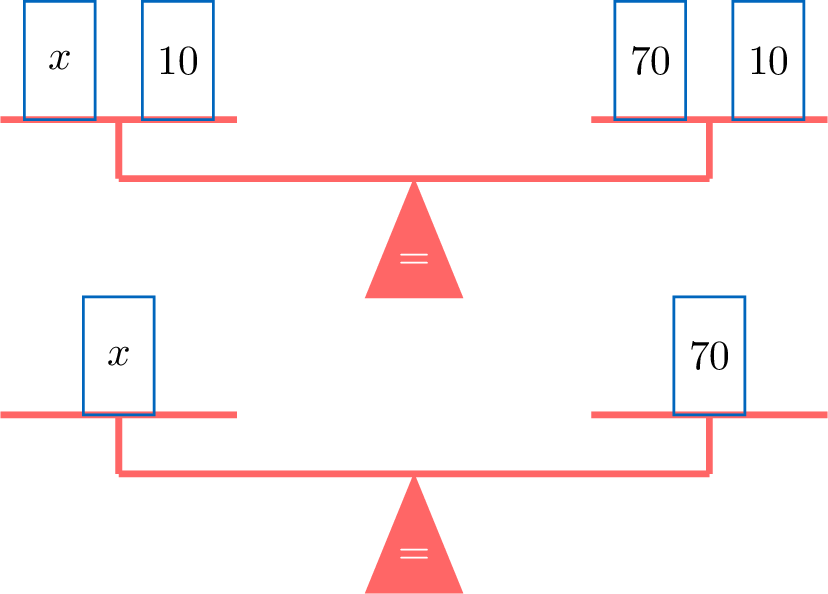
- Multiplying or dividing both sides by the same (nonzero) number
Equation Balance scale \(2x = 70\) 
Divide both sides by 2 Divide the weight into two equal parts \(\begin{aligned}\frac{2x}{2} &= \frac{70}{2} \\x &= 35\end{aligned}\) 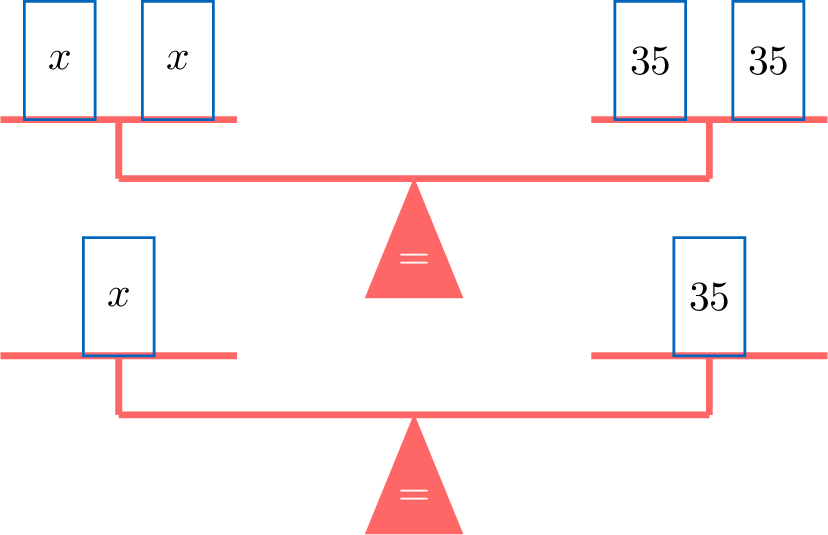
Doing and Undoing Expressions
Proposition Doing an Expression
To do an expression, perform the operations in order.
Example
To do the expression \(2x + 1\), start with \(x\), multiply by 2, then add 1:$$\boxed{x}\xrightarrow{\times 2}\boxed{2x}\xrightarrow{+1}\boxed{2x+1} $$
Definition Inverse Operations
- Adding and subtracting are inverse operations:
\(\boxed{x}\xrightarrow{+a}\boxed{x+a}\xrightarrow{-a}\boxed{x}$$x + a = b \quad \Longleftrightarrow \quad x = b - a$$\) - Multiplying and dividing are inverse operations:
\(\boxed{x}\xrightarrow{\times a}\boxed{ax}\xrightarrow{\div a}\boxed{x}$$a \times x = c \quad \Longleftrightarrow \quad x = c \div a$$\)
Method Undoing an Expression
To undo an expression, use inverse operations in reverse order.
Example
To undo the expression \(2x + 1\), start with \(2x + 1\), subtract \(1\), then divide by \(2\):$$\boxed{2x + 1}\xrightarrow{-1}\boxed{2x}\xrightarrow{\div 2}\boxed{x} $$
Solving Linear Equations
Method Inverse Operations
If the unknown appears only once in the equation, we use inverse operations to simplify the expression and isolate the unknown.
Example
Solve for \(x\):$$2x+1=7$$
To solve \(2x + 1 = 7\):
- To do the expression \(2x + 1\): $$ \boxed{x}\xrightarrow{\times 2}\boxed{2x}\xrightarrow{+1}\boxed{2x+1} $$
- To undo the expression \(2x + 1\): $$ \boxed{2x + 1}\xrightarrow{-1}\boxed{2x}\xrightarrow{\div 2}\boxed{x} $$
- Step by step: $$ \begin{aligned} 2x + 1 &= 7 \\ 2x + 1 - 1 &= 7 - 1 \qquad &\text{(subtracting 1 from both sides)} \\ 2x &= 6 \\ \dfrac{2x}{2} &= \dfrac{6}{2} \qquad &\text{(dividing both sides by 2)} \\ x &= 3 \end{aligned} $$
- So the solution is \(x = 3\).