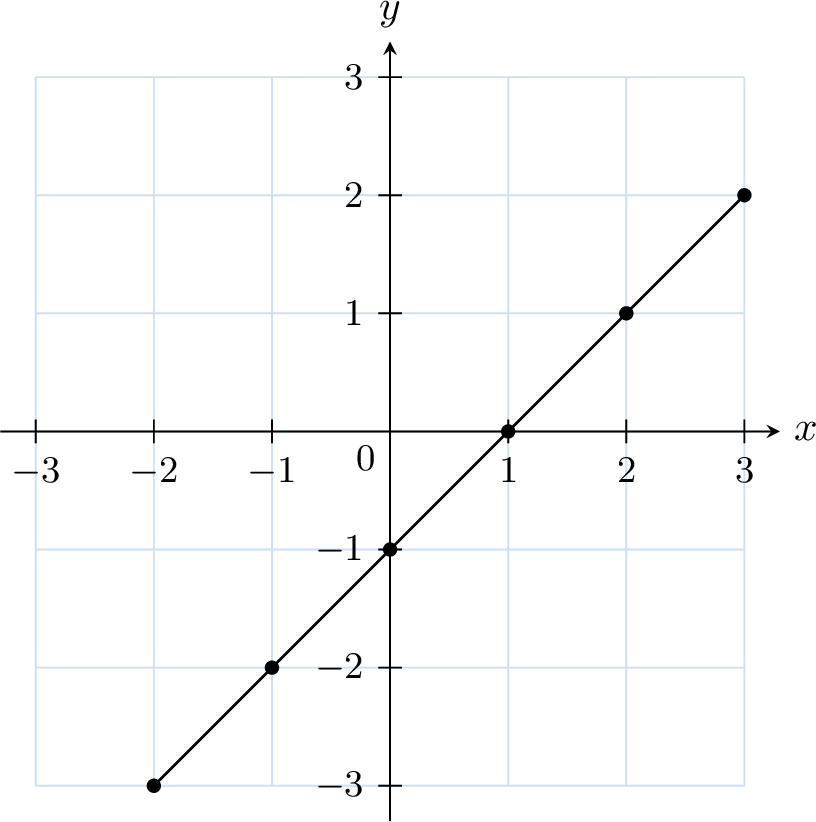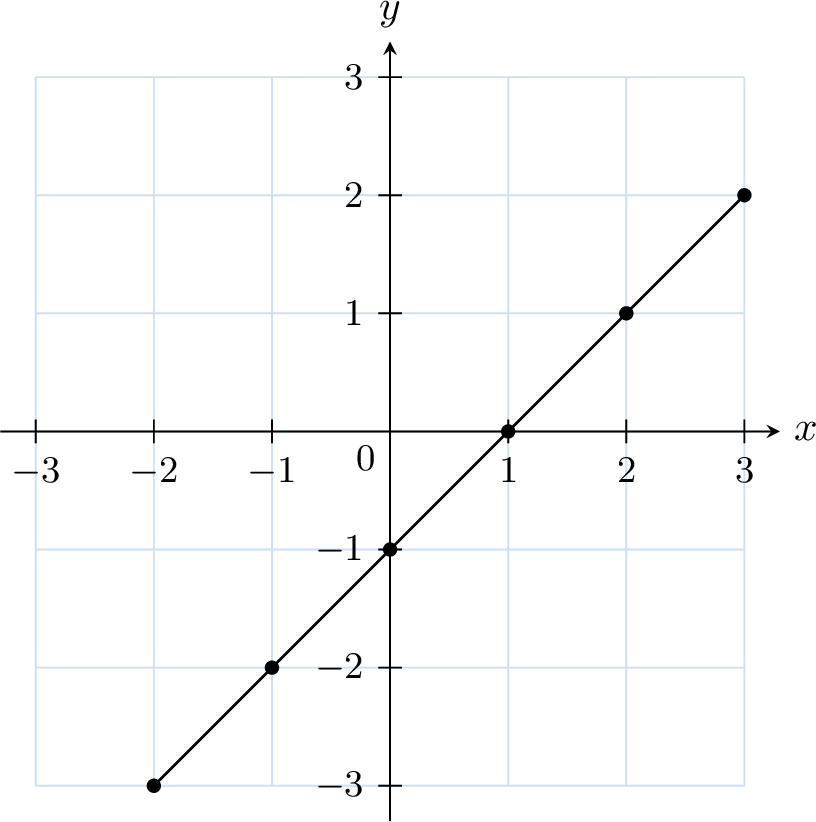Functions

Definitions

A function is like a machine that produces an output from an input according to a rule.

To represent this machine, we write $\textcolor{olive}{f}(\textcolor{colordef}{\text{input}}) = \textcolor{colorprop}{\text{output}}$. The brackets $($ $)$ indicate the action of the function $\textcolor{olive}{f}$ on the input.
We use function notation to name functions and their variables, replacing "$\textcolor{colordef}{\text{input}}$" by "$\textcolor{colordef}{x}$" and "$\textcolor{colorprop}{\text{output}}$" by "$\textcolor{colorprop}{f(x)}$".
For example, if the rule is "twice the input":

we have $\textcolor{olive}{f}(\textcolor{colordef}{x}) = 2 \times \textcolor{colordef}{x}$.
When the input is $\textcolor{colordef}{x} = \textcolor{colordef}{1}$, we get:$$\begin{aligned}\textcolor{olive}{f}(\textcolor{colordef}{1}) &= 2 \times \textcolor{colordef}{(1)}\\ &= \textcolor{colorprop}{2}\end{aligned}$$The table of values below shows the output values for different input values:

Definition Function

From an input value $x$, a function $f$ produces an output value $f(x)$.
$f(x)$ is read as "$f$ of $x$".

Example

For $f(x)=2x-1$ (the function that doubles the input and subtracts 1), find $f(5)$.

Answer

$\begin{aligned}[t] f(5)&=2\times (5)-1&(\text{substituting } x \text{ by } (5))\\&=9 \end{aligned}$

Tables of Values

Definition Table of Values

The table of values for a function $f$ provides a listing of pairs $(x, f(x))$, where $x$ is an input value and $f(x)$ is the corresponding output value produced by the function $f$.

Example

For $f(x)=x^2$, complete the following table:

$x$	$-2$	$-1$	$0$	$1$	$2$
$f(x)$

Answer

$\begin{aligned}[t] f(-2) &= (-2)^2 & (\text{substituting } x \text{ by } (-2)) \\ &= 4 \end{aligned}$
$\begin{aligned}[t] f(-1) &= (-1)^2 & (\text{substituting } x \text{ by } (-1)) \\ &= 1 \end{aligned}$
$\begin{aligned}[t] f(0) &= (0)^2 & (\text{substituting } x \text{ by } (0)) \\ &= 0 \end{aligned}$
$\begin{aligned}[t] f(1) &= (1)^2 & (\text{substituting } x \text{ by } (1)) \\ &= 1 \end{aligned}$
$\begin{aligned}[t] f(2) &= (2)^2 & (\text{substituting } x \text{ by } (2)) \\ &= 4 \end{aligned}$

So the completed table is:

$x$	$-2$	$-1$	$0$	$1$	$2$
$f(x)$	$4$	$1$	$0$	$1$	$4$

Graphs

Definition Graph

A graph of a function is the set of all points $(\textcolor{colordef}{x},\textcolor{colordef}{f(x)})$ in the plane, where $x$ is an input and $f(x)$ is its output.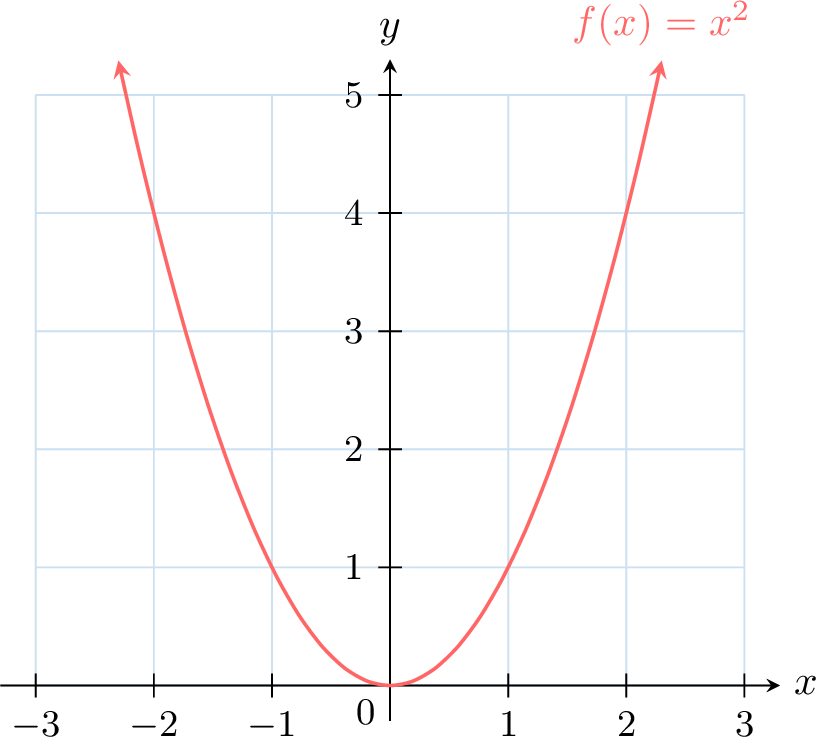

Method Finding the value $f(x)$ using a graph

To find $f(2)$ on a graph, follow these steps:

Locate the $x$-value: Find $x = 2$ on the $x$-axis.
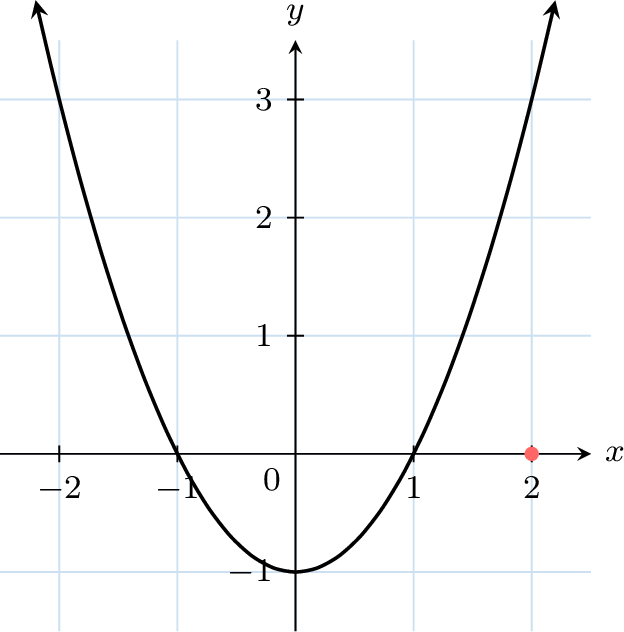
Move vertically to the curve: From $x = 2$, draw a vertical line up to the graph.
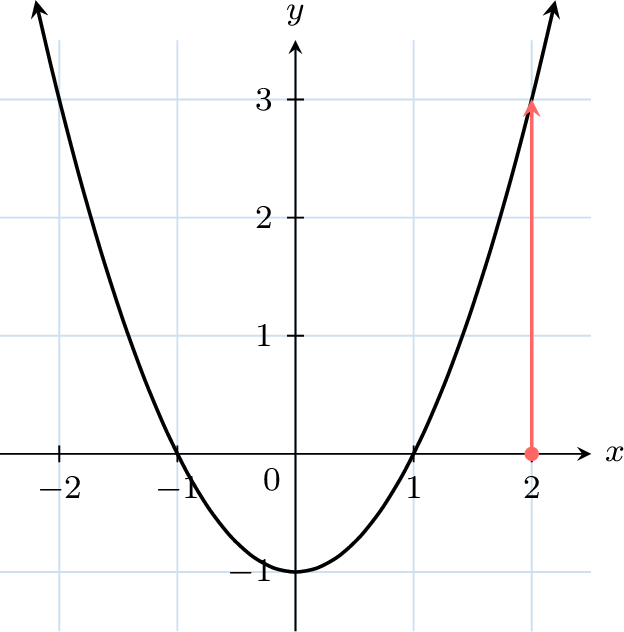
Read the $y$-value: At the intersection with the curve, move horizontally to the $y$-axis to find the value $f(2)$.

Thus, $f(2) = 3$.

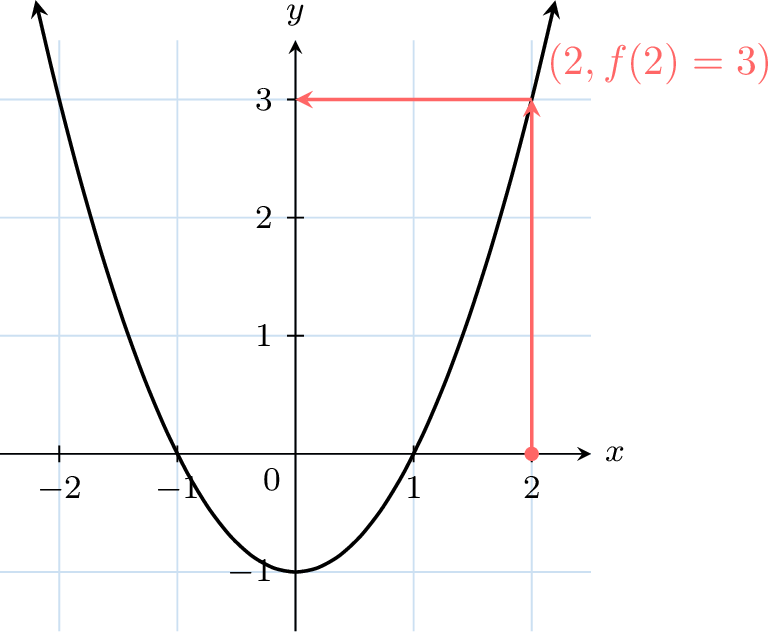
Method Plotting a Line Graph from a Table

To plot the graph of a function from a table of values, follow these steps:

Plot each point $(\textcolor{colordef}{x},\textcolor{colorprop}{f(x)})$ from the table onto the coordinate plane.
Connect the points with straight line segments.

Example

Here is a table of values for the function $f(x) = x - 1$:

$x$	$-2$	$-1$	$0$	$1$	$2$	$3$
$f(x)$	$-3$	$-2$	$-1$	$0$	$1$	$2$

Plot the line graph of $f$.

Answer

Plot the points $(-2, -3)$, $(-1, -2)$, $(0, -1)$, $(1, 0)$, $(2, 1)$, and $(3, 2)$. Then, connect the points with straight segments to form the line graph.

\(x\)	\(-2\)	\(-1\)	\(0\)	\(1\)	\(2\)
\(f(x)\)

\(x\)	\(-2\)	\(-1\)	\(0\)	\(1\)	\(2\)
\(f(x)\)	\(4\)	\(1\)	\(0\)	\(1\)	\(4\)

\(x\)	\(-2\)	\(-1\)	\(0\)	\(1\)	\(2\)	\(3\)
\(f(x)\)	\(-3\)	\(-2\)	\(-1\)	\(0\)	\(1\)	\(2\)