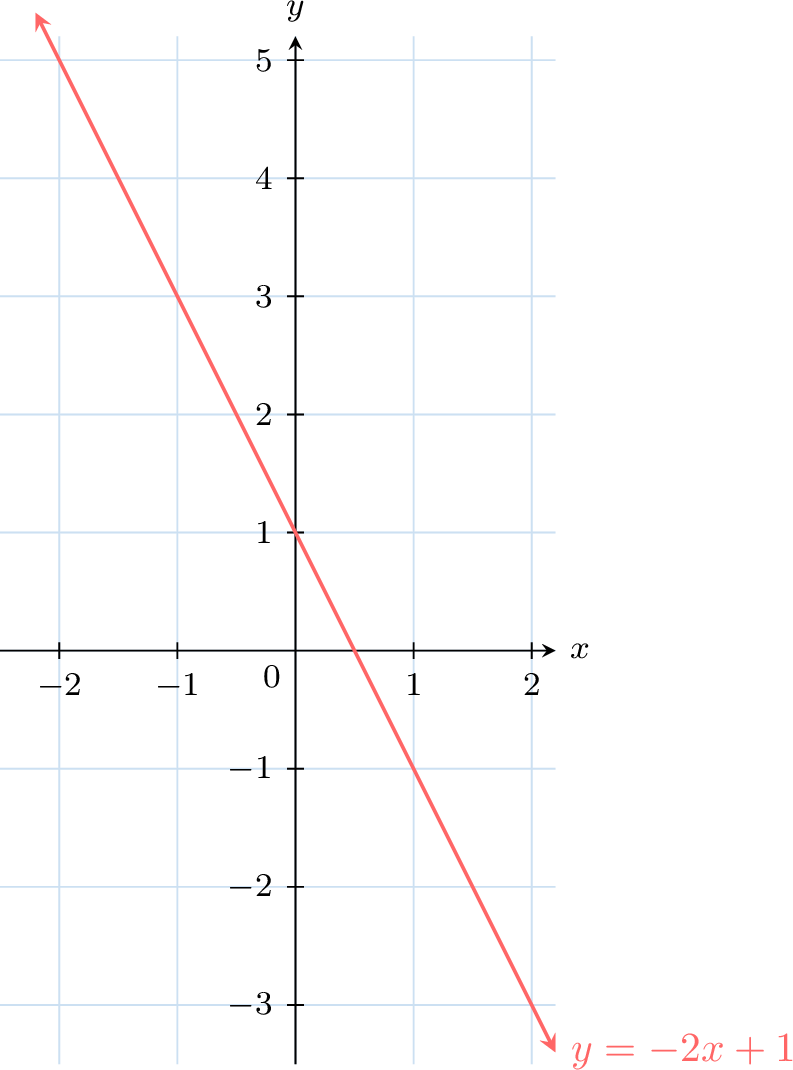Line Equations

Consider the equation \(\textcolor{colorprop}{y}=2\textcolor{colordef}{x}-1\), which describes the relationship between two variables \(\textcolor{colordef}{x}\) and \(\textcolor{colorprop}{y}\).
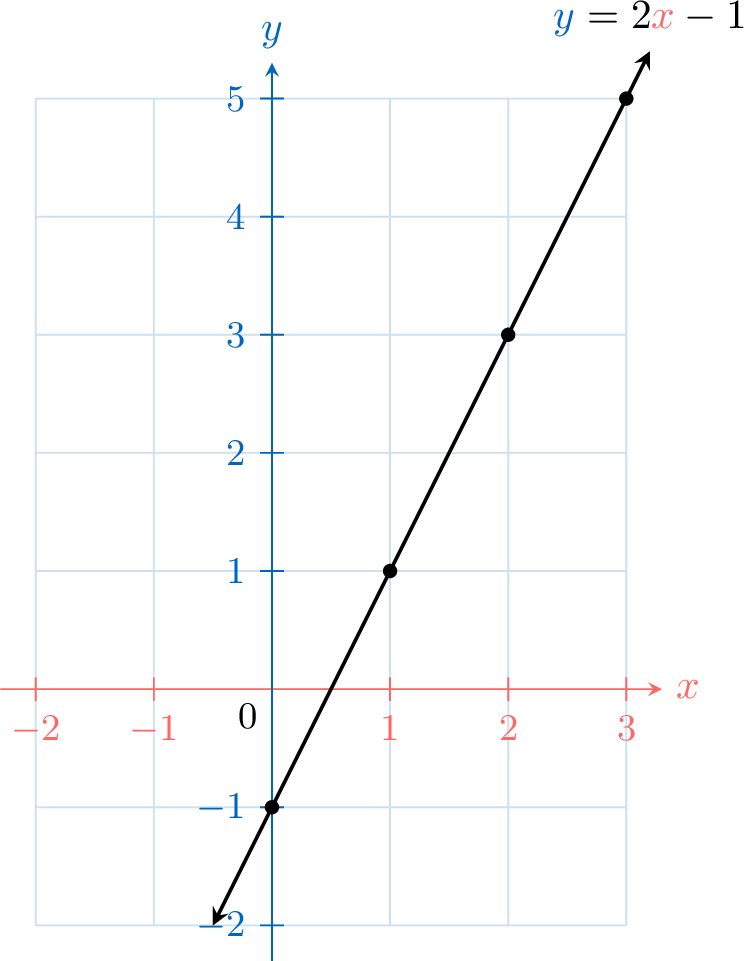
For any given value of \(\textcolor{colordef}{x}\), we can use the equation to find the corresponding value of \(\textcolor{colorprop}{y}\). These values give coordinates \((\textcolor{colordef}{x}, \textcolor{colorprop}{y})\) of points on the graph.

• For \(\textcolor{colordef}{x} = \textcolor{colordef}{1}\):$$\begin{aligned}[t]\textcolor{colorprop}{y} &= 2\times \textcolor{colordef}{1} - 1 \\ &= \textcolor{colorprop}{1}\end{aligned}$$
• For \(\textcolor{colordef}{x} = \textcolor{colordef}{2}\):$$\begin{aligned}[t]\textcolor{colorprop}{y} &= 2\times \textcolor{colordef}{2} - 1 \\ &= \textcolor{colorprop}{3}\end{aligned}$$

From calculations like these, we can construct a table of values:

\(\textcolor{colordef}{x}\)	\(\textcolor{colordef}{0}\)	\(\textcolor{colordef}{1}\)	\(\textcolor{colordef}{2}\)	\(\textcolor{colordef}{3}\)
\(\textcolor{colorprop}{y}\)	\(\textcolor{colorprop}{-1}\)	\(\textcolor{colorprop}{1}\)	\(\textcolor{colorprop}{3}\)	\(\textcolor{colorprop}{5}\)

So, the points \((\textcolor{colordef}{0},\textcolor{colorprop}{-1})\), \((\textcolor{colordef}{1},\textcolor{colorprop}{1})\), \((\textcolor{colordef}{2},\textcolor{colorprop}{3})\), and \((\textcolor{colordef}{3},\textcolor{colorprop}{5})\) all lie on the graph.
In fact, there are infinitely many points that satisfy \(\textcolor{colorprop}{y}=2 \textcolor{colordef}{x}-1\), forming a continuous line extending indefinitely in both directions (indicated with arrowheads).\(\textcolor{colorprop}{y}=2 \textcolor{colordef}{x}-1\) is an equation that relates \(x\) and \(y\) for all points on the line.