Roots
Square Roots
- When we square a number, we multiply it by itself.
For example, 3 squared is \(3 \times 3\), which can be written as \(3^2\).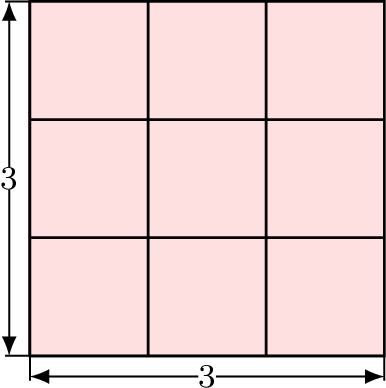
\(3^2=9\) is the area of a square with side length \(3\). - On the other hand, taking the square root of a number is the reverse process: it is finding a number that, when multiplied by itself, gives the original number. For example,
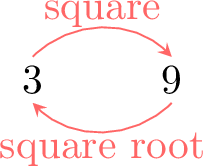
3 squared is 9, so the square root of 9 is 3.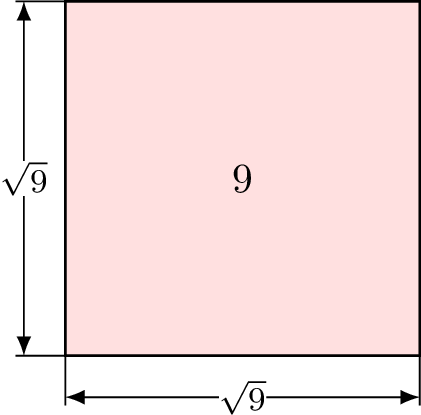
The square root of \(9\), written as \(\sqrt{9}\), is the side length of a square with area 9.
Definition Square root
The square root of \(a\), written \(\sqrt{a}\), is the positive number which, when squared, gives \(a\):$$\left(\sqrt{a}\right)^2 =\sqrt{a} \times \sqrt{a}=a$$
Example
Find \(\sqrt{25}\).
Since \(5 \times 5 = 25\), \(\sqrt{25}=5\).
Definition Perfect Squares
A perfect square is a number that is the result of squaring an integer.
Example
The perfect squares of the first few integers are:
1, 4, 9, 16, 25, 36, 49, 64, and so on.
1, 4, 9, 16, 25, 36, 49, 64, and so on.
Definition Simplest square root Form
A square root is written in simplest form if the number under the square root sign is as small as possible.
Calculating Square Roots
It is easy to calculate the square root of a perfect square, but determining the square root of other numbers can be quite challenging.
Method Use a calculator
- Press the square root button \(\boxed{\sqrt{\;}}\)
- Enter the number
- Press the equals button \(\boxed{=}\)
By entering \(\sqrt{10}\) and pressing the equals button, the calculator displays: \(3.16227766017\).
So \(\sqrt{10} \approx 3.2\).
So \(\sqrt{10} \approx 3.2\).
Cube Root
Definition Cube Root
The cube root of \(a\), written \(\sqrt[3]{a}\), is the number which, when cubed, gives \(a\):$$\left(\sqrt[3]{a}\right)^3=a$$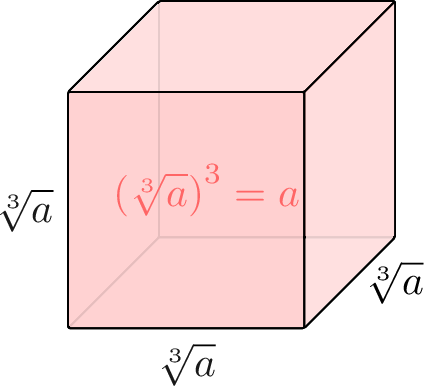
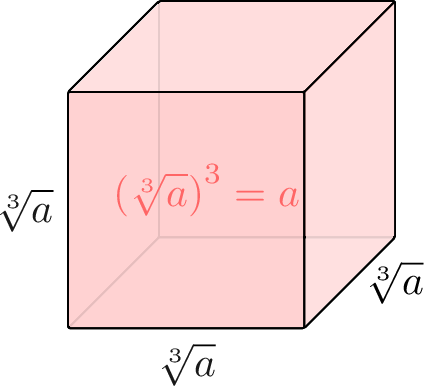
Example
Find \(\sqrt[3]{125}\).
As \(5 \times 5\times 5=125\), \(\sqrt[3]{125}=5\).
Laws of Square Roots
Proposition Law 1
For two positive numbers \(a\) and \(b\):$$ \sqrt{a} \cdot \sqrt{b} = \sqrt{ab} $$
$$\begin{aligned}[t]\left(\sqrt{a} \cdot \sqrt{b}\right)^2 &= \left(\sqrt{a} \cdot \sqrt{b}\right) \cdot \left(\sqrt{a} \cdot \sqrt{b}\right) \\
&= \left(\sqrt{a} \cdot \sqrt{a}\right) \cdot \left(\sqrt{b} \cdot \sqrt{b}\right) \\
&= ab\end{aligned}$$So, by definition, \(\sqrt{a} \cdot \sqrt{b}\) is the square root of \(ab\). Therefore, \(\sqrt{a} \cdot \sqrt{b} = \sqrt{ab}\).
Example
Show that \(\sqrt{6} = \sqrt{2} \cdot \sqrt{3}\).
$$\begin{aligned}[t]\sqrt{6} &= \sqrt{2 \times 3} \\
&= \sqrt{2} \cdot \sqrt{3}\end{aligned}$$
Proposition Law 2 (Perfect Square)
For a positive number \(a\):$$ \sqrt{a^2} = a $$$$ \sqrt{a \cdot a} = a $$
$$\begin{aligned}[t]\sqrt{a^2} &= \sqrt{a \cdot a} \\
&= \sqrt{a} \cdot \sqrt{a} && \text{(by Law 1)} \\
&= \left(\sqrt{a}\right)^2 \\
&= a && \text{(by definition of the square root)}\end{aligned}$$
Example
Find \(\sqrt{25}\).
$$\begin{aligned}[t]\sqrt{25} &= \sqrt{5 \times 5} \\
&= 5 && \text{(extract one number of the pair from the square root)}\end{aligned}$$
Proposition Law 3
For two positive numbers \(a\) and \(b\):$$ \sqrt{a^2 b} = a \sqrt{b} $$$$ \sqrt{a \cdot a \cdot b} = a \sqrt{b} $$
$$\begin{aligned}[t]\sqrt{a^2 b} &= \sqrt{a^2} \cdot \sqrt{b} && \text{(by Law 1)} \\
&= a \sqrt{b} && \text{(by Law 2)}\end{aligned}$$
Example
Simplify \(\sqrt{12} = 2 \sqrt{3}\).
$$\begin{aligned}[t]\sqrt{12} &= \sqrt{2 \times 2 \times 3} \\
&= 2 \sqrt{3} && \text{(extract one number of the pair from the square root)}\end{aligned}$$
Proposition Law 4
For two positive numbers \(a\) and \(b\):$$ \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} $$
$$\begin{aligned}[t]\left(\frac{\sqrt{a}}{\sqrt{b}}\right)^2 &= \frac{\sqrt{a}}{\sqrt{b}} \cdot \frac{\sqrt{a}}{\sqrt{b}} \\
&= \frac{\sqrt{a} \cdot \sqrt{a}}{\sqrt{b} \cdot \sqrt{b}} \\
&= \frac{a}{b}\end{aligned}$$So, by definition, \(\frac{\sqrt{a}}{\sqrt{b}}\) is the square root of \(\frac{a}{b}\). Therefore, \(\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}\).
Example
Simplify \(\dfrac{\sqrt{6}}{\sqrt{3}}\).
$$\begin{aligned}[t]\frac{\sqrt{6}}{\sqrt{3}} &= \sqrt{\frac{6}{3}} \\
&= \sqrt{2}\end{aligned}$$
Algebraic Operations
Proposition Algebraic Operations
We can perform operations with square roots just as we do with ordinary numbers. In particular:
- We can add and subtract like square roots (i.e., same number under the root) in the same way that we add and subtract like algebraic terms.
- We can use the usual rules for expanding brackets.
Example
Simplify: \(2 \sqrt{3}+4 \sqrt{3}\)
$$\begin{aligned}[t]2 \sqrt{3}+4 \sqrt{3} &= (2+4)\sqrt{3} \quad \text{(factorisation)} \\
&= 6 \sqrt{3}\end{aligned}$$