Properties of Integers
Numbers 1 and 0
Zero (0) and one (1) are very special numbers which have important properties.
Proposition Additive Identity Property
Adding \(0\) to any number results in the number itself.
For any number \(a\),$$0+a=a$$
For any number \(a\),$$0+a=a$$
Example
\(7+0=7\)
Proposition Multiplicative Identity Property
Multiplying \(1\) by any number results in the number itself.
For any number \(a\),$$ 1\times a=a$$
For any number \(a\),$$ 1\times a=a$$
Example
\(1\times 7=7\)
- Multiplying by \(0\):
- Any number multiplied by 0 always results in 0.
- For example, \(5 \times 0 = 0 + 0 + 0 + 0 + 0 = 0\).
- Dividing by \(0\):
- Division by \(0\) is undefined in mathematics because it leads to a contradiction.
- For example, if \(a = 5 \div 0\), then \( a \times 0 = 5\). But this is impossible because \(a \times 0\) is always 0, not 5.
Proposition Multiplying by \(0\)
For any number \(a\),$$a\times 0 =0$$
Proposition Dividing by \(0\)
Division by \(0\) is undefined.
Division with Remainders
Theorem Division with Remainder
For any integers \(\textcolor{olive}{a}\) and nonzero \(\textcolor{colordef}{b}\), there exist unique integers \(\textcolor{colorprop}{q}\) and \(\textcolor{orange}{r}\) such that:$$\textcolor{olive}{a} = \textcolor{colordef}{b} \times \textcolor{colorprop}{q} + \textcolor{orange}{r} \quad \text{with} \quad 0\leq \textcolor{orange}{r} < \textcolor{colordef}{b}$$
- \(\textcolor{olive}{a}\) is the \(\textcolor{olive}{\text{dividend}}\) (the number to be shared),
- \(\textcolor{colordef}{b}\) is the \(\textcolor{colordef}{\text{divisor}}\) (the number of groups),
- \(\textcolor{colorprop}{q}\) is the \(\textcolor{colorprop}{\text{quotient}}\) (the size of each group),
- \(\textcolor{orange}{r}\) is the \(\textcolor{orange}{\text{remainder}}\).
Example
$$\begin{array}{ccccccccl} \textcolor{olive}{13} &=& \textcolor{colordef}{3}& \times& \textcolor{colorprop}{4}&+&\textcolor{orange}{1} & \text{with }& \textcolor{orange}{1}\lt \textcolor{colordef}{3}\\
\textcolor{olive}{\text{Dividend}}&=& \textcolor{colordef}{\text{Divisor}}&\times&\textcolor{colorprop}{\text{Quotient}}&+&\textcolor{orange}{\text{Remainder}}& \text{with }& \textcolor{orange}{\text{Remainder}}\lt \textcolor{colordef}{\text{Divisor}} \end{array} $$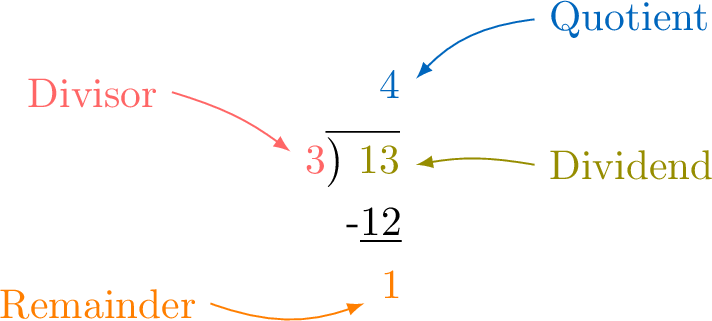
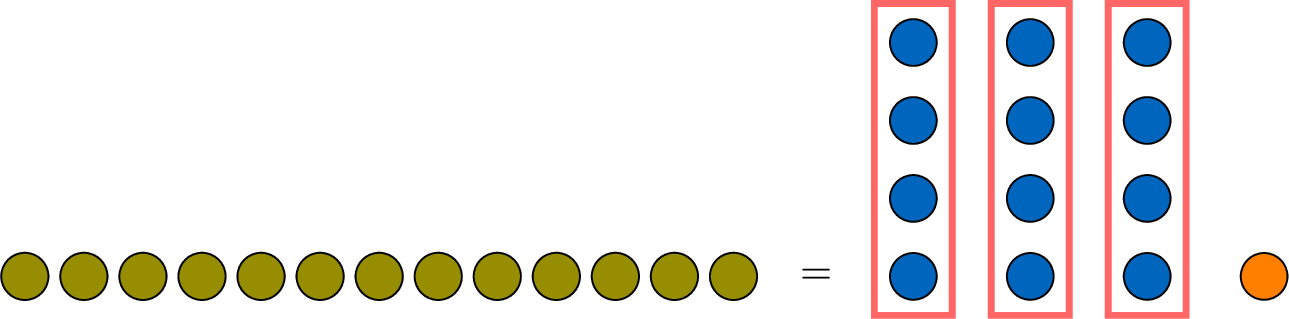
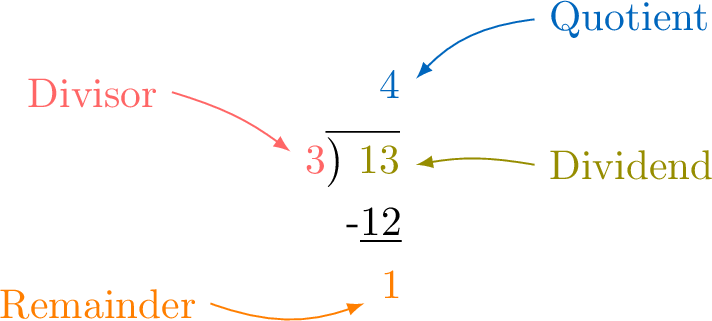
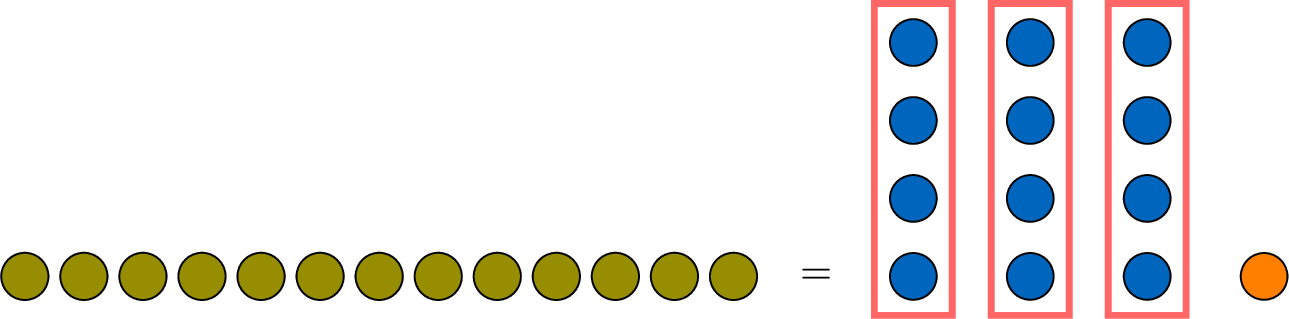
Divisibility
Definition Divisible
A whole number is said to be divisible by another non-zero whole number if the remainder is zero when you divide the first number by the second number. In this case, we say that the second number is a divisor of the first number.
Example
Is \(10\) divisible by \(5\)?
Yes, \(\textcolor{olive}{10}\) is divisible by \(\textcolor{colordef}{5}\) because the remainder of the division is \(\textcolor{orange}{0}\): \(\textcolor{olive}{10} = \textcolor{colordef}{5} \times \textcolor{colorprop}{2} + \textcolor{orange}{0}\).
Example
Is \(13\) divisible by \(5\)?
No, \(\textcolor{olive}{13}\) is not divisible by \(\textcolor{colordef}{5}\) because the remainder of the division is \(\textcolor{orange}{3}\): \(\textcolor{olive}{13} = \textcolor{colordef}{5} \times \textcolor{colorprop}{2} + \textcolor{orange}{3}\).
Definition Multiple
A whole number is said to be a multiple of another non-zero whole number if the first number can be obtained by multiplying the second number by some whole number. In other words, the first number appears in the multiplication table of the second number. In this case, we say that the second number is a factor of the first number.
Example
Is \(10\) a multiple of \(5\)?
Yes, \(10\) is a multiple of \(5\) because \(5 \times 2 = 10\). So \(5\) is a factor of \(10\).
Theorem Divisible \(\Leftrightarrow\) Multiple
For two whole numbers, the first number is divisible by the second number if and only if the first number is a multiple of the second number.
This is a direct consequence of the uniqueness of the quotient and remainder in the division with remainder theorem. If the remainder is zero, then the dividend is exactly the product of the divisor and the quotient, which is the definition of a multiple. Conversely, if a number is a multiple of another, then by definition it can be written as a product, implying a zero remainder upon division.
Example
Is \(1000\) divisible by \(10\)?
Yes, as \(1000 = 100 \times 10\), \(1000\) is a multiple of \(10\). Therefore, \(1000\) is divisible by \(10\).
Divisibility Criteria
Divisibility criteria are methods that allow us to quickly determine if a whole number is divisible by another whole number without performing long division. These rules are useful for simplifying calculations and understanding number properties. Here are some common divisibility criteria:
Proposition Divisibility Criteria for 2 and 5
- A number is divisible by 2 if its last digit is even (0, 2, 4, 6, or 8).
- A number is divisible by 5 if its last digit is 0 or 5.
Example
Determine whether \(946\) is divisible by \(2\).
\(946\) is divisible by \(2\) because its last digit is \(6\), which is even.
Example
Determine whether \(947\) is divisible by \(5\).
\(947\) is not divisible by \(5\) because its last digit is \(7\), which is not \(0\) or \(5\).
Proposition Divisibility Criteria for 3 and 9
- A number is divisible by 3 if the sum of its digits is divisible by 3.
- A number is divisible by 9 if the sum of its digits is divisible by 9.
Example
Determine whether \(948\) is divisible by \(3\).
\(948\) is divisible by \(3\) because the sum of its digits, \(9 + 4 + 8 = 21\), is divisible by \(3\) (\(21 = 3 \times 7\)).
Example
Determine whether \(948\) is divisible by \(9\).
\(948\) is not divisible by \(9\) because the sum of its digits, \(9 + 4 + 8 = 21\), is not divisible by \(9\) (\(21 = 9 \times 2 + 3\)).
Proposition Divisibility Criteria for 4
A number is divisible by 4 if the number formed by its last two digits is divisible by 4.
Example
Determine whether \(917\) is divisible by \(4\).
\(917\) is not divisible by \(4\) because the number formed by its last two digits, \(17\), is not divisible by \(4\) (\(17 = 4 \times 4 + 1\)).
Prime number
Definition Prime Number
A prime number is a whole number greater than 1 that has only two different divisors: 1 and itself.
A whole number greater than 1 that is not prime is called a composite number.
A whole number greater than 1 that is not prime is called a composite number.
Example
State whether \(6\) is a prime number.
As \(2\times 3=6\), \(6\) is not a prime number because it is divisible by \(2\) and \(3\), in addition to \(1\) and \(6\). So \(6\) is a composite number.
Example
State whether \(5\) is a prime number.
\(5\) is a prime number because it is divisible entirely only by \(1\) and \(5\). We cannot divide it entirely by \(2, 3\) or \(4\) (there would be a remainder).
Proposition First 25 Prime Numbers
Here is the list of the first 25 prime numbers:$$ 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97$$
Prime factorization
Definition Prime Factorization
Prime factorization is writing a number as a product of only prime numbers. In other words, it's finding which prime numbers you need to multiply together to get the original number.
Example
Find the prime factorization of \(12\).
The prime factorization is \(12=2\times 2 \times 3\).
The order is not important. You can write \(12=3\times 2 \times 2\).
The prime factorization is not \(12=2\times 6\) as \(6\) is a composite number.
The order is not important. You can write \(12=3\times 2 \times 2\).
The prime factorization is not \(12=2\times 6\) as \(6\) is a composite number.
Method Factor Tree
The Factor tree method involves breaking down a composite number into smaller factors, then breaking down those factors further until you have only prime factors.
- Place the number at the top of the factor tree.
- Check if the number is prime.
- If the number is prime: Circle it. You are done with this branch.
- If the number is composite: Factorize it into two smaller factors. Write these two factors as branches below the number. Repeat step 2 for each of these new factors.
- The prime factorization is the product of all circled prime numbers on the tree.
Example
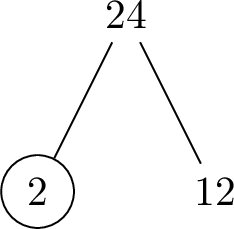
Find a prime factorization of \(24\).
- Step 1:

- Step 2: \(24\) is a composite number. \(24=2\times 12\).
- Step 3: \(12\) is a composite number. \(12=2\times 6\).
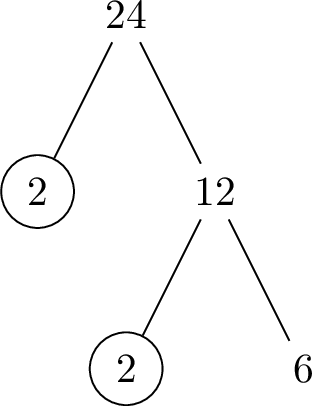
- Step 4: \(6\) is a composite number. \(6=2\times 3\).
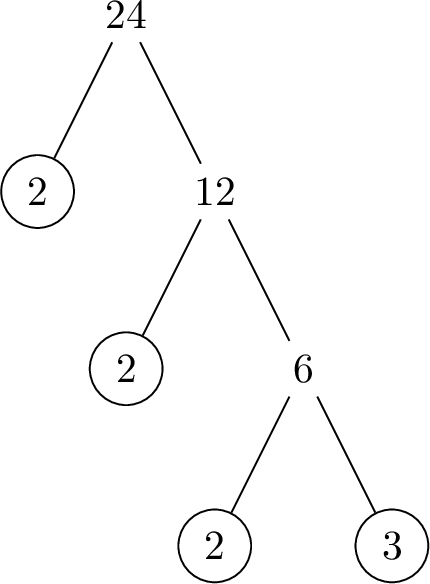
Greatest Common Divisor (GCD)
Definition Greatest Common Divisor (GCD)
The greatest common divisor (GCD) of two (or more) whole numbers is the largest positive integer that divides each of them exactly (with remainder \(0\)). It is also called the highest common factor (HCF).
Example
Find the GCD of \(18\) and \(24\).
- The divisors of \(18\) are: \(1, 2, 3, \textcolor{olive}{6}, 9, 18\).
- The divisors of \(24\) are: \(1, 2, 3, 4, \textcolor{olive}{6}, 8, 12, 24\).
- The greatest common divisor is \(\textcolor{olive}{6}\).
Method Finding GCD Using Prime Factorization
- Write the prime factorization of each number.
- Box the prime factors that appear in both numbers.
- Multiply these common factors to get the GCD.
Example
Find the GCD of \(18\) and \(24\) using prime factorization.
- \(18 = \boxed{2} \times \boxed{3} \times 3\)
- \(24 = \boxed{2}\times 2 \times 2 \times \boxed{3}\)
- Common prime factors: \(\boxed{2}\) and \(\boxed{3}\)
- So, \(\gcd(18, 24) = 2 \times 3 = 6\)
Least Common Multiple (LCM)
Definition Least Common Multiple (LCM)
The least common multiple (LCM) of two (or more) whole numbers is the smallest positive integer that is a multiple of each of them. It is also called the lowest common multiple.
Example
Find the LCM of \(8\) and \(12\).
- The multiples of \(8\) are: \(8, 16, \textcolor{olive}{24}, 32, 40, \ldots\)
- The multiples of \(12\) are: \(12, \textcolor{olive}{24}, 36, 48, \ldots\)
- The least common multiple is \(\textcolor{olive}{24}\).
Method Finding LCM Using Prime Factorization
- Write the prime factorization of each number.
- For each prime, take the highest power that appears in either number.
- Multiply these together to get the LCM.
Example
Find the LCM of \(8\) and \(12\) using prime factorization.
- \(8 = 2^3\)
- \(12 = 2^2 \times 3^1\)
- Take the highest powers: \(2^3\) and \(3^1\)
- So, \(LCM(8, 12) = 2^3 \times 3^1 = 8 \times 3 = 24\)