Expansion
In mathematics, we often want to transform the form of an expression to make it easier to work with, to simplify calculations, or to solve equations. Expand is the process of writing an expression as a sum of terms by distributing multiplication over addition.
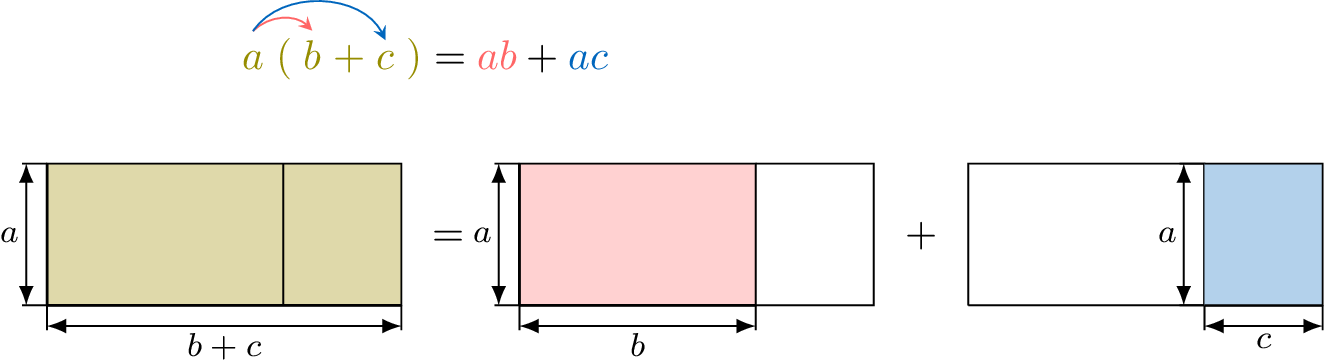
Distributive Law 1
Proposition Distributive Law 1
Multiplication is distributive over addition and subtraction:
- Addition:
- Subtraction:
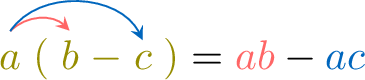
Example
Expand and simplify \(2(l + L)\).
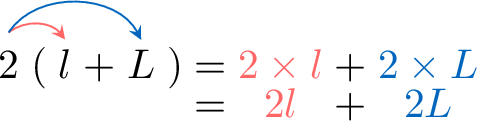
Distributive Law 2
Proposition Distributive law 2
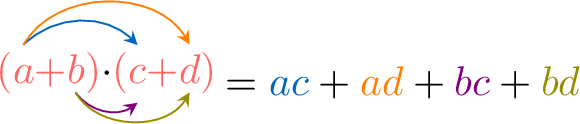

Example
Expand and simplify \((x+4)(2x+2)\)
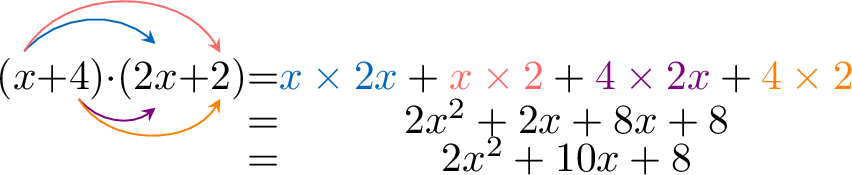
Difference of Two Squares
Proposition Difference of Two Squares
$$(\textcolor{colordef}{a}-\textcolor{colorprop}{b})(\textcolor{colordef}{a}+\textcolor{colorprop}{b}) =\textcolor{colordef}{a}^2-\textcolor{colorprop}{b}^2 $$
$$\begin{aligned}(a-b)(b+a) & = a b+aa-bb-b a & &\text {(expanding)} \\
& = \cancel{ab}+a^2-b^2-\cancel{ab} & & \\
&= a^2-b^2 &&\\
\end{aligned}$$
Example
Expand and simplify: \((x-3)(x+3)\).
$$\begin{aligned}(\textcolor{colordef}{x}-\textcolor{colorprop}{3})(\textcolor{colordef}{x}+\textcolor{colorprop}{3}) & = \textcolor{colordef}{x}^2-\textcolor{colorprop}{3}^2 \\
& = x^2-9\\
\end{aligned}$$
Perfect Squares Expansion
Proposition Perfect Squares Expansion
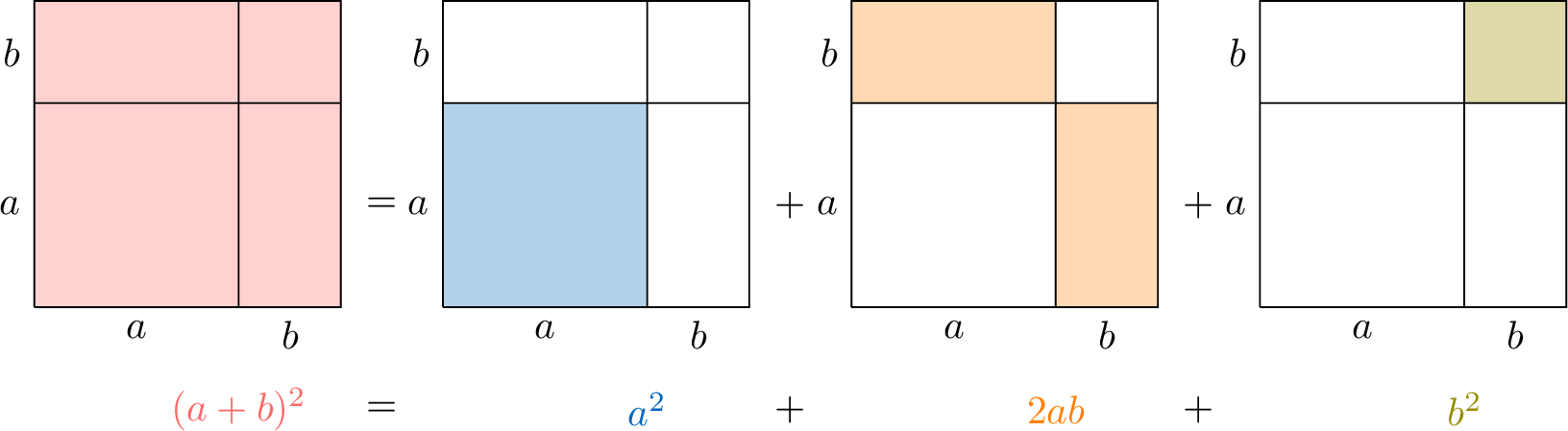
$$\begin{aligned}(a+b)^2 & =(a+b) (a+b) &&\text {(square definition)} \\
&= a a+ab+ba+b b & &\text {(expanding)} \\
&= a^2+2ab+b^2 &&\text {(combining)}\\
\end{aligned}$$and$$\begin{aligned}(a-b)^2 & =(a-b) (a-b) &&\text {(square definition)} \\
&= a a-ab-ba+b b & &\text {(expanding)} \\
&= a^2-2ab+b^2 &&\text {(combining)}\\
\end{aligned}$$
Example
Expand and simplify \((x+2)^2\)
In the perfect squares expansion, we substitute \(a=x\) and \(b=2\):$$\begin{aligned}(\textcolor{colordef}{x}+\textcolor{colorprop}{2})^{2} &=\textcolor{colordef}{x}^{2}+2 \times \textcolor{colordef}{x} \times \textcolor{colorprop}{2}+\textcolor{colorprop}{2}^{2} \\
&=x^{2}+4 x+4\end{aligned}$$