Formulas
Definitions
Formulas are important tools in various branches of mathematics. They help us understand and model real-world situations, solve problems, and make predictions.
Definition Formula
A formula is an equation that connects two or more variables.
Example
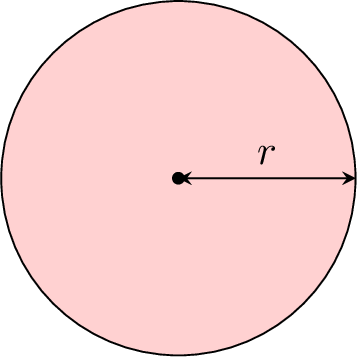
Example
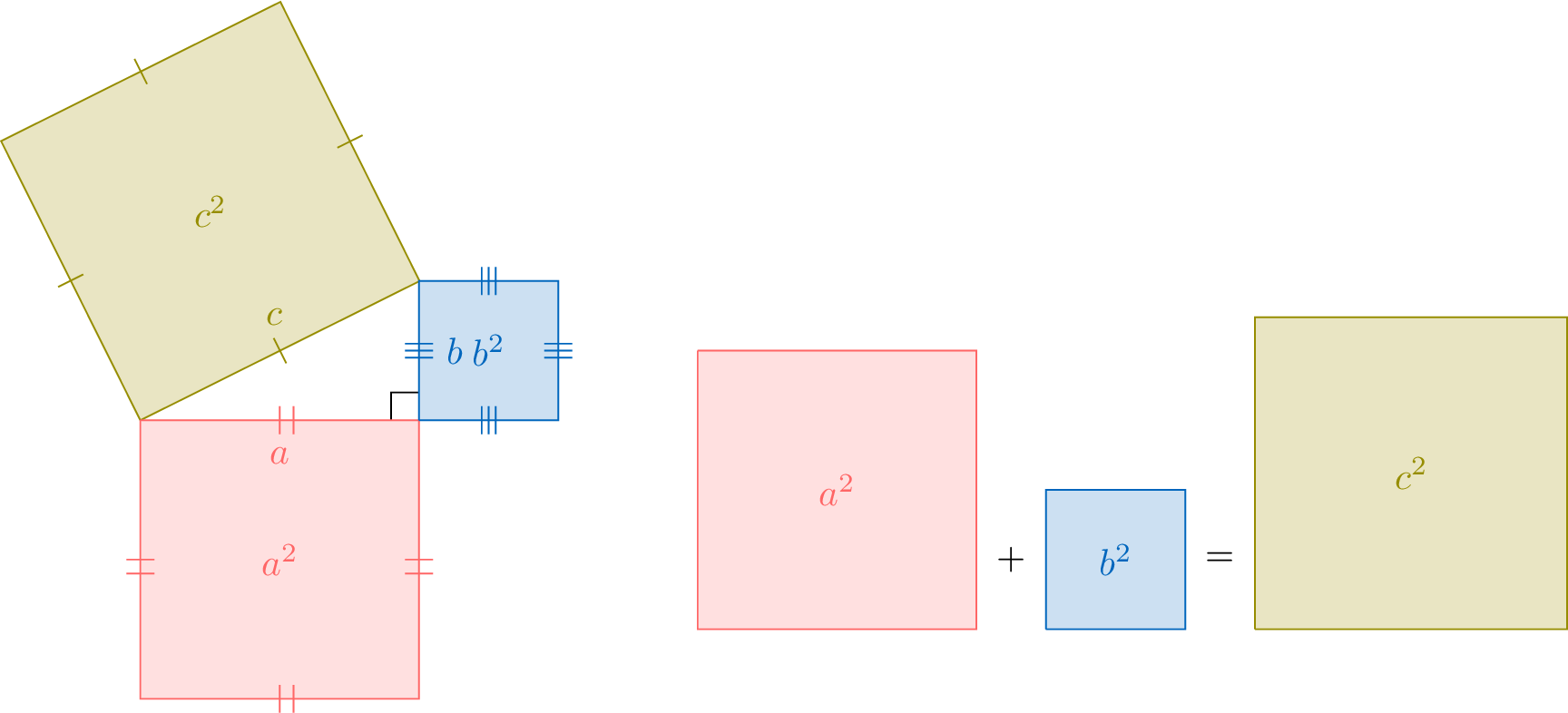
Example
The formula \(v = \dfrac{d}{t}\) relates distance \(d\), velocity \(v\), and time \(t\).
Definition Subject of a Formula
The subject of a formula is the variable that is expressed in terms of other variables. It is usually placed on the left side of the equation and separated from the other variables by an equal sign \((=)\).
Example
Find the subject of the formula \(A = \pi r^2\).
The subject of the formula is the area \(A\).
Problem Solving
Method Problem Solving
- Identify the formula: Determine which formula is appropriate for the given problem or context. The formula should include the variable you want to evaluate and any other required variables or constants.
- Substitute the known values: Replace the variables in the formula with their corresponding values.
- Solve: Perform the necessary mathematical operations to isolate the variable you want to evaluate. This may involve simplifying expressions, combining like terms, applying arithmetic operations, or using algebraic techniques such as factoring or the quadratic formula.
- Check your result: Once you have found the value of the variable, check it to ensure it is reasonable and makes sense in the context of the problem. This may involve substituting the value back into the original equation to verify that it satisfies the conditions.
Example
Find the side length of a square with an area equal to \(16 \mathrm{~m}^2\).
- Identify the formula: The area of a square is \(A = s^2\), where \(A\) is the area and \(s\) is the side length.
- Substitute the known values: Here, \(A = 16\,\text{m}^2\), so \(16 = s^2\).
- Solve for the unknown variable: Take the square root of both sides:$$\begin{aligned}s^2 &= 16 \\ s &= \sqrt{16} \qquad (s > 0) \\ s &= 4\ \text{m}\end{aligned}$$
- Check your result: \((4)^2 = 16\), so \(s = 4\,\text{m}\) is correct.
Rearranging Formulae
Method Changing the Subject of a Formula
Using algebraic rules, you can rearrange a formula so that another variable is the subject.
Example
For the equation for the area of a square \(A = s^2\), find the equation where \(s\) is the subject.
$$\begin{aligned}A &= s^2 \\
\sqrt{A} &= s \qquad (\text{take the positive square root}) \\
s &= \sqrt{A}\end{aligned}$$
Constructing Formulae
Method Constructing Formulae
- Identify the variables: Determine which variables you need to represent the quantities in the problem.
- Define the relationship: Understand the relationship between the variables and constants, and how they are connected.
- Use operations: Apply the appropriate mathematical operations to connect the variables and constants.
- Write the equality: Write the equation that represents the relationship between the variables and constants.
Example
A mechanic charges a \(\\)40\( call-out fee and \)\\(30\) per hour thereafter.
Find the mechanic's fee \(M\) for a job that takes \(x\) hours.
Find the mechanic's fee \(M\) for a job that takes \(x\) hours.
The total fee is \(\\)40\( plus \)\\(30\) for each hour \(x\):
- For \(x = 1\), \(M = 40 + 30 \times 1\)
- For \(x = 2\), \(M = 40 + 30 \times 2\)
- \(\vdots\)
- For \(x\), \(M = 40 + 30 \times x\)
Method Conjecturing Formulae by Special Cases
Formulas can be conjectured by generalizing patterns observed in specific numerical cases.
Example
Area of a rectangle:
- Special values:
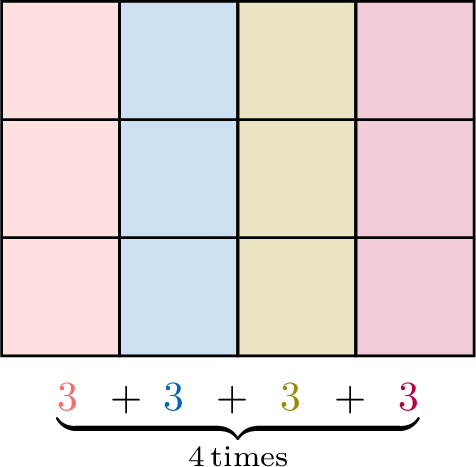
- General case:
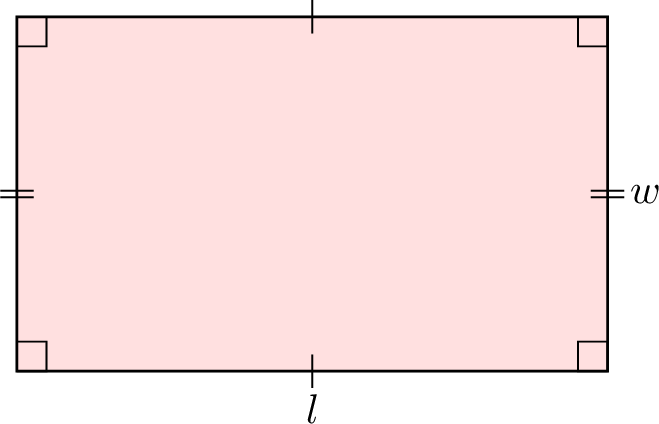
Example
Examine the matchstick diagrams:

Observe the pattern and count the matchsticks in each diagram:
- Diagram \(1\) has \(3 = 3 \times 1\).
- Diagram \(2\) has \(6 = 3 \times 2\).
- Diagram \(3\) has \(9 = 3 \times 3\).
- \(\vdots\)
- Diagram \(n\) has \(3 \times n\).