Linear Functions

Definition

Definition Linear Function

A linear function is defined by:$$f(x) = ax + b$$where $a$ is the slope, and $b$ is the $y$-intercept.

Example

Access to a swimming pool costs a fixed entrance fee of $\dollar$12, plus $\dollar$5 for each hour you stay. Let $P(x)$ be the total price for $x$ hours at the pool. Find a formula for $P(x)$.

Answer

The total cost is $\dollar$12 for entry plus $\dollar$5 for each of $x$ hours:

For $ \textcolor{colordef}{x=1}$, $P(\textcolor{colordef}{1}) = 12 + 5 \times \textcolor{colordef}{1}$
For $ \textcolor{colordef}{x=2}$, $P(\textcolor{colordef}{2}) = 12 + 5 \times \textcolor{colordef}{2}$
$\vdots$
For $ \textcolor{colordef}{x}$, $P(\textcolor{colordef}{x}) = 12 + 5 \times \textcolor{colordef}{x}$

Graph

Proposition Graph

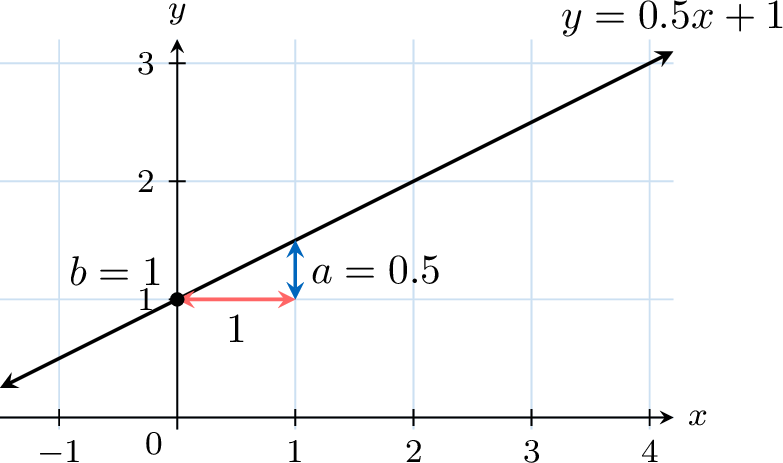
The graph of a linear function $f(x) = ax + b$ is a straight line of equation $y = ax + b$, where $a$ is the slope and $b$ is the $y$-intercept.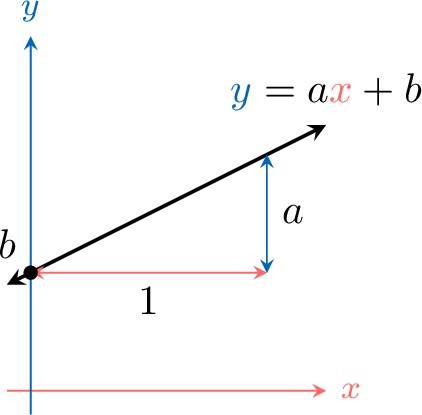

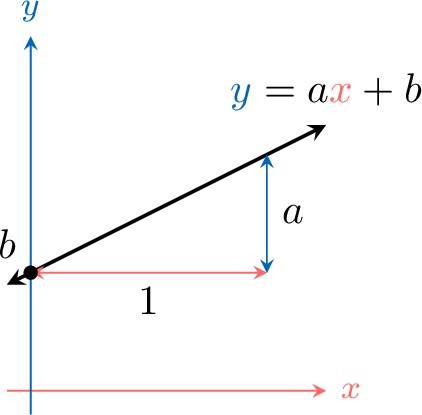
Example

For the function $f(x)=0.5x+1$, draw its graph.

Answer