Trigonometry
Trigonometry is a branch of mathematics that studies the relationships between the side lengths and angles of triangles, especially right-angled triangles. It is widely used in science, engineering, astronomy, and even video game development. The foundation of trigonometry lies in three main ratios: sine, cosine, and tangent.
Right-Angled Triangle
Definition Right-Angled Triangle
A right-angled triangle is a triangle with one angle equal to \(90^\circ\). For a given angle \(\theta\) (other than the right angle), we define: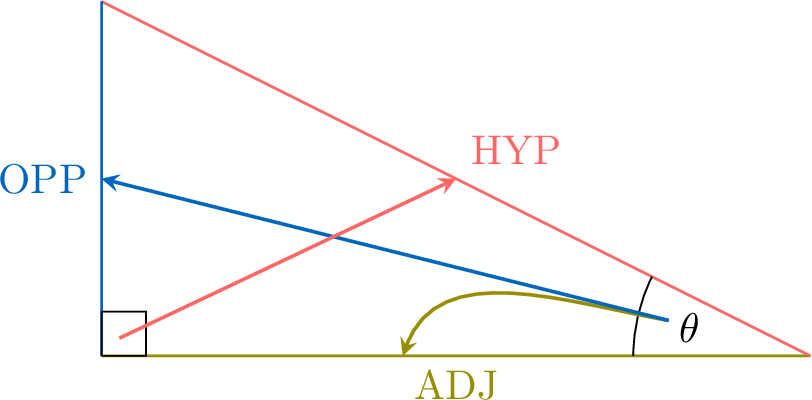
- Hypotenuse (HYP): The longest side, opposite the right angle.
- Adjacent Side (ADJ): The side next to the angle \(\theta\), which is not the hypotenuse.
- Opposite Side (OPP): The side facing the angle \(\theta\).

Example
In the triangle below, identify the hypotenuse, the adjacent side, and the opposite side relative to angle \(\theta\).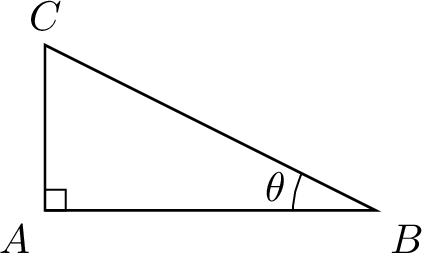

- Hypotenuse: \(\Segment{BC}\)
- Adjacent side: \(\Segment{AC}\)
- Opposite side: \(\Segment{AB}\)
Trigonometric Functions
- Using a protractor and ruler, draw right-angled triangles with one angle \(\theta\) equal to \(15^\circ\), \(30^\circ\), \(45^\circ\), \(60^\circ\), or \(75^\circ\). Measure the lengths of the hypotenuse and the adjacent side to the nearest millimeter.
- Complete the following table with the ratio \(\frac{\text{ADJ}}{\text{HYP}}\) for each angle:
\(\theta\) \(15^\circ\) \(30^\circ\) \(45^\circ\) \(60^\circ\) \(75^\circ\) \(\dfrac{\text{ADJ}}{\text{HYP}}\)
- Here are examples of right-angled triangles for the specified angles. In each triangle, the side adjacent to \(\theta\) (ADJ) and the hypotenuse (HYP) are labeled so you can measure and verify the ratios.
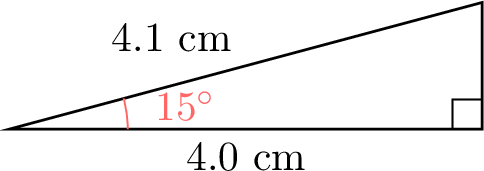
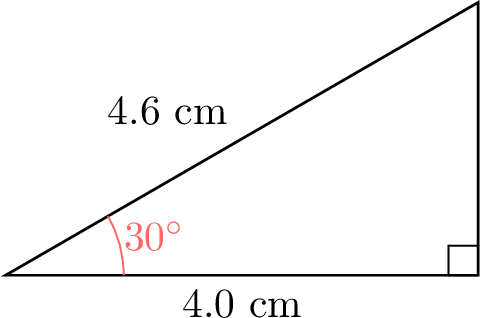
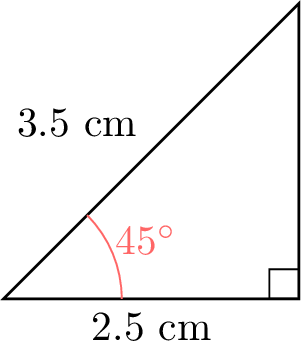
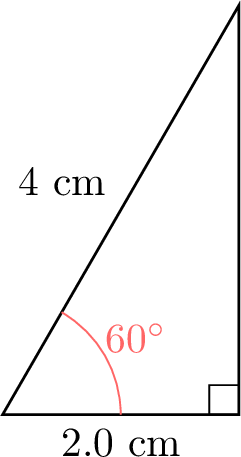
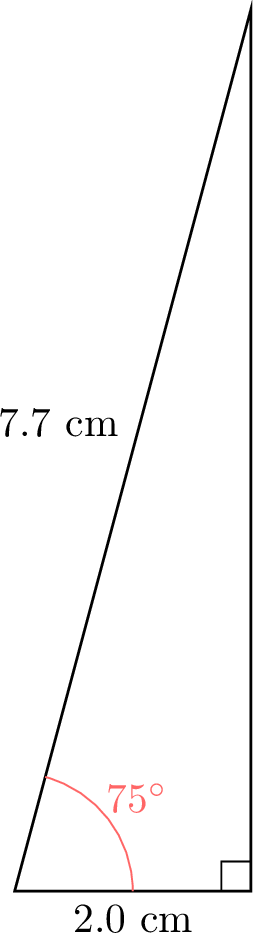
- The ratio \(\dfrac{\text{ADJ}}{\text{HYP}}\) for each angle, using a calculator:
\(\theta\) \(15^\circ\) \(30^\circ\) \(45^\circ\) \(60^\circ\) \(75^\circ\) \(\dfrac{\text{ADJ}}{\text{HYP}}\) \(0.97\) \(0.87\) \(0.71\) \(0.50\) \(0.26\)
Proposition Trigonometric Ratios
For any two right-angled triangles with the same angle \(\theta\), the ratios \(\dfrac{\text{OPP}}{\text{HYP}}\), \(\dfrac{\text{ADJ}}{\text{HYP}}\), and \(\dfrac{\text{OPP}}{\text{ADJ}}\) are constant.
Consider two right-angled triangles with the same angle \(\theta\). Since their angles are equal, the triangles are similar. Therefore, the ratios are constant for a given angle.
This means that for any right-angled triangle with the same angle \(\theta\), the ratio \(\dfrac{\text{ADJ}}{\text{HYP}}\) is always the same. This is why we define the cosine function, denoted \(\cos\), such that:$$\cos(\theta) = \frac{\text{ADJ}}{\text{HYP}}$$For example:
| \(\theta\) | \(15^\circ\) | \(30^\circ\) | \(45^\circ\) | \(60^\circ\) | \(75^\circ\) |
| \(\cos(\theta)\) | \(0.97\) | \(0.87\) | \(0.71\) | \(0.50\) | \(0.26\) |
Definition Trigonometric Functions
In a right-angled triangle with angle \(\theta\):$$\sin(\theta) = \frac{\text{OPP}}{\text{HYP}}, \quad\cos(\theta) = \frac{\text{ADJ}}{\text{HYP}}, \quad\tan(\theta) = \frac{\text{OPP}}{\text{ADJ}}$$
The mnemonic SOH-CAH-TOA helps remember the definitions:
- Sine = Opposite \(\div\) Hypotenuse
- Cosine = Adjacent \(\div\) Hypotenuse
- Tangent = Opposite \(\div\) Adjacent
Example
In the triangle below, find \(\cos \theta\), \(\sin \theta\), and \(\tan \theta\).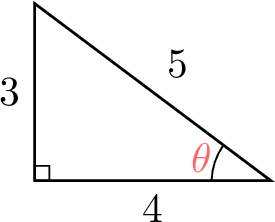

Relative to \(\theta\):
- Hypotenuse: \(BC = 5\)
- Adjacent side: \(AB = 4\)
- Opposite side: \(AC = 3\)
Proposition Tangent Formula
$$\tan \theta = \frac{\sin \theta}{\cos \theta}$$
$$\frac{\sin \theta}{\cos \theta}= \frac{\dfrac{\text{OPP}}{\text{HYP}}}{\dfrac{\text{ADJ}}{\text{HYP}}}= \frac{\text{OPP}}{\text{HYP}} \times \frac{\text{HYP}}{\text{ADJ}}= \frac{\text{OPP}}{\text{ADJ}}= \tan \theta$$
Method Using Calculator
Trigonometric ratios for any angle can be calculated using a calculator in degree mode. Make sure your calculator is set to "degrees" before calculating.
Example
In the triangle below, find \(x\).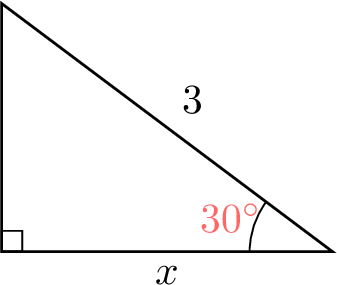

$$\begin{aligned}\cos \theta &= \frac{\text{ADJ}}{\text{HYP}} \\
\cos(30^\circ) &= \frac{x}{3} \\
x &= 3 \times \cos(30^\circ) \\
x &\approx 3 \times 0.866 \\
x &\approx 2.6\,\text{cm}\end{aligned}$$
Inverse Trigonometric Functions
Trigonometric ratios can be used to find unknown angles in right-angled triangles when at least two side lengths are known.
Definition Inverse Trigonometric Functions
In a right-angled triangle with an angle \(\theta\):$$\theta = \cos^{-1}\left(\frac{\text{ADJ}}{\text{HYP}}\right), \quad\theta = \sin^{-1}\left(\frac{\text{OPP}}{\text{HYP}}\right), \quad\theta = \tan^{-1}\left(\frac{\text{OPP}}{\text{ADJ}}\right)$$
Example
In the triangle below, find the angle \(\theta\).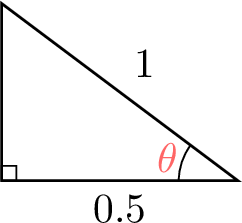

We know the lengths of the adjacent side (\(AB = 0.5\)) and the hypotenuse (\(BC = 1\)) relative to \(\theta\). We can use the inverse cosine function:$$\begin{aligned}\theta &= \cos^{-1}\left(\frac{\text{ADJ}}{\text{HYP}}\right) \\
&= \cos^{-1}\left(\frac{0.5}{1}\right) \\
&= 60^\circ\end{aligned}$$
Solving Real-World Trigonometry Problems
Trigonometric ratios are powerful tools for solving a wide range of problems involving right-angled triangles, especially in real-world contexts.To solve these problems effectively, follow the structured steps below:
Method Solving Real-World Trigonometry Problems
- Draw a clear diagram representing the situation described in the problem.
- Label the unknown (side or angle) you need to find. Use \(x\) for a side and \(\theta\) for an angle if possible.
- Identify a right-angled triangle within your diagram.
- Write an equation relating an angle and two sides of the triangle using the appropriate trigonometric ratio.
- Solve the equation to find the unknown value.
- State your answer clearly, including appropriate units, in a complete sentence.