Functions
Definitions
A function is like a machine that produces an output from an input according to a rule.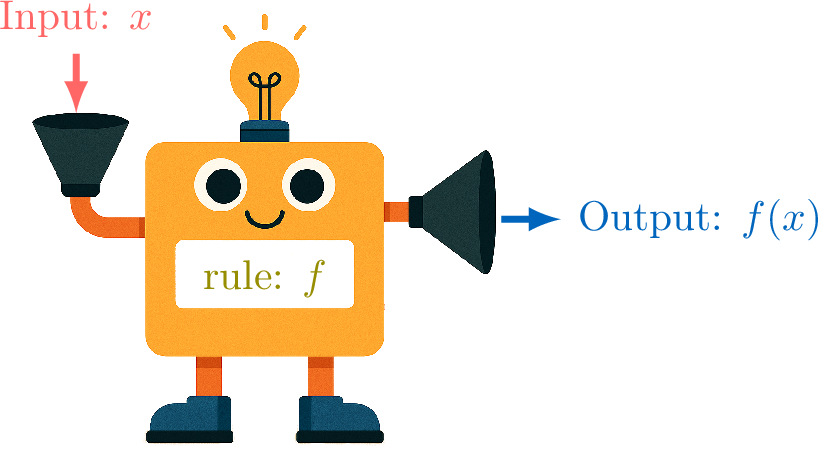
We use function notation to name functions and their variables, replacing "\(\textcolor{colordef}{\text{input}}\)" by "\(\textcolor{colordef}{x}\)" and "\(\textcolor{colorprop}{\text{output}}\)" by "\(\textcolor{colorprop}{f(x)}\)".
We can write this function as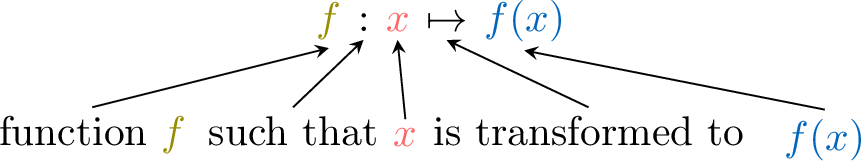

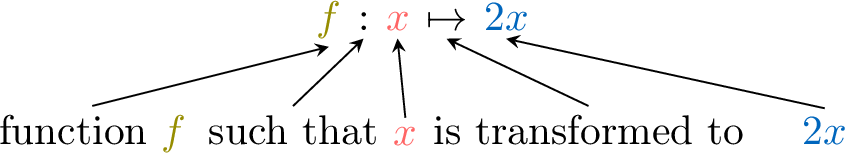


We use function notation to name functions and their variables, replacing "\(\textcolor{colordef}{\text{input}}\)" by "\(\textcolor{colordef}{x}\)" and "\(\textcolor{colorprop}{\text{output}}\)" by "\(\textcolor{colorprop}{f(x)}\)".
We can write this function as
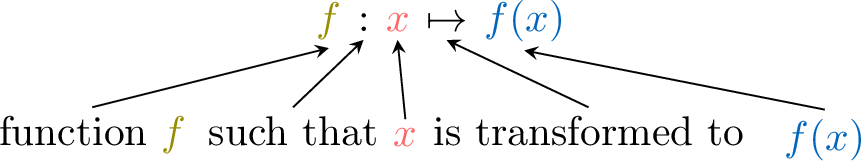

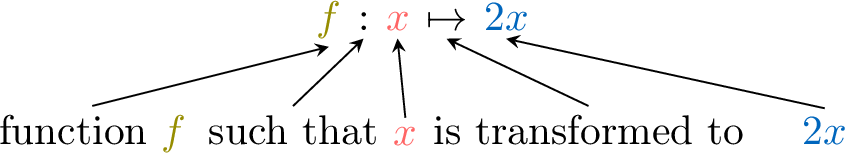

Definition Function
From an input value \(x\), a function \(f\) produces an output value \(f(x)\).
We can write:
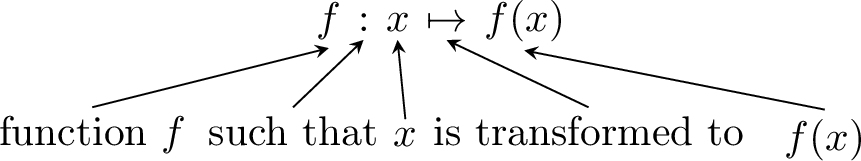
We can write:

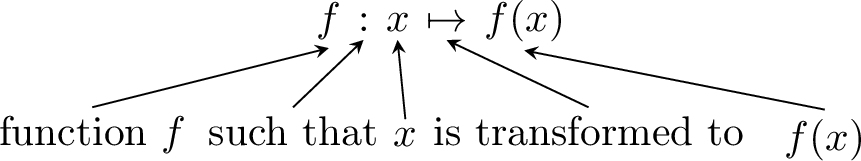
- \(f(x)\) is read as "\(f\) of \(x\)".
- \(f(x)\) is called the image of \(x\).
Example
For \(f(x)=2x-1\) (the function that doubles the input and subtracts 1), find \(f(5)\).
\(\begin{aligned}[t] f(5)&=2\times (5)-1&(\text{substituting } x \text{ by } (5))\\&=9 \end{aligned}\)
Tables of Values
Definition Table of Values
The table of values for a function \(f\) provides a listing of pairs \((x, f(x))\), where \(x\) is an input value and \(f(x)\) is the corresponding output value produced by the function \(f\).
Example
For \(f(x)=x^2\), complete the following table:
| \(x\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) |
| \(f(x)\) |
- \(\begin{aligned}[t] f(-2) &= (-2)^2 & (\text{substituting } x \text{ by } (-2)) \\ &= 4 \end{aligned}\)
- \(\begin{aligned}[t] f(-1) &= (-1)^2 & (\text{substituting } x \text{ by } (-1)) \\ &= 1 \end{aligned}\)
- \(\begin{aligned}[t] f(0) &= (0)^2 & (\text{substituting } x \text{ by } (0)) \\ &= 0 \end{aligned}\)
- \(\begin{aligned}[t] f(1) &= (1)^2 & (\text{substituting } x \text{ by } (1)) \\ &= 1 \end{aligned}\)
- \(\begin{aligned}[t] f(2) &= (2)^2 & (\text{substituting } x \text{ by } (2)) \\ &= 4 \end{aligned}\)
| \(x\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) |
| \(f(x)\) | \(4\) | \(1\) | \(0\) | \(1\) | \(4\) |
Graphs
Definition Graph
A graph of a function is the set of all points \((\textcolor{colordef}{x},\textcolor{colordef}{f(x)})\) in the plane, where \(x\) is an input and \(f(x)\) is its output.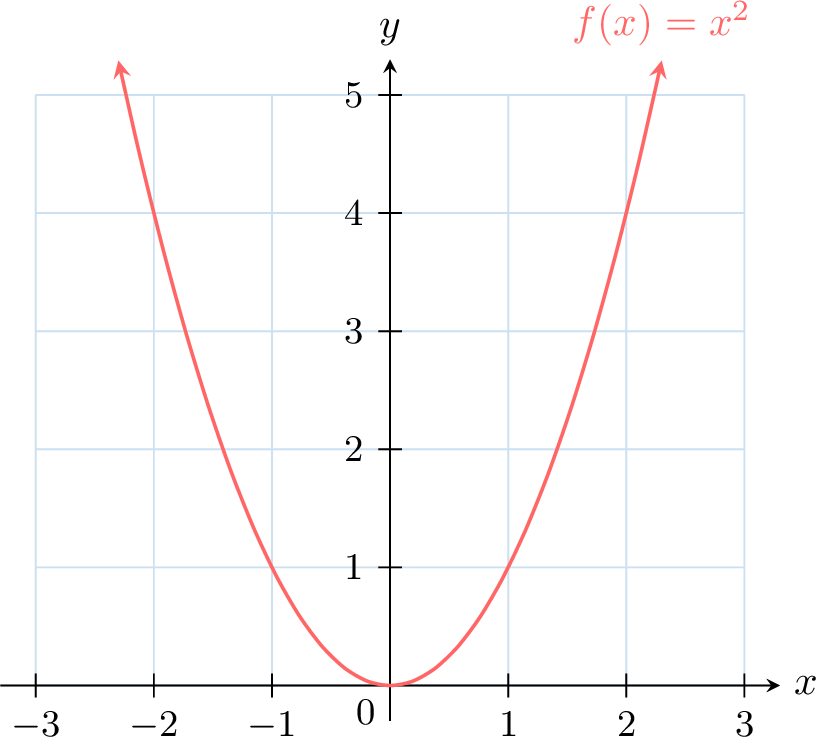

Method Plotting a Line Graph from a Table
To plot the graph of a function from a table of values, follow these steps:
- Plot each point \((\textcolor{colordef}{x},\textcolor{colorprop}{f(x)})\) from the table onto the coordinate plane.
- Connect the points with straight line segments.
Example
Here is a table of values for the function \(f(x) = x - 1\):
| \(x\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) |
| \(f(x)\) | \(-3\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) |
Plot the points \((-2, -3)\), \((-1, -2)\), \((0, -1)\), \((1, 0)\), \((2, 1)\), and \((3, 2)\). Then, connect the points with straight segments to form the line graph.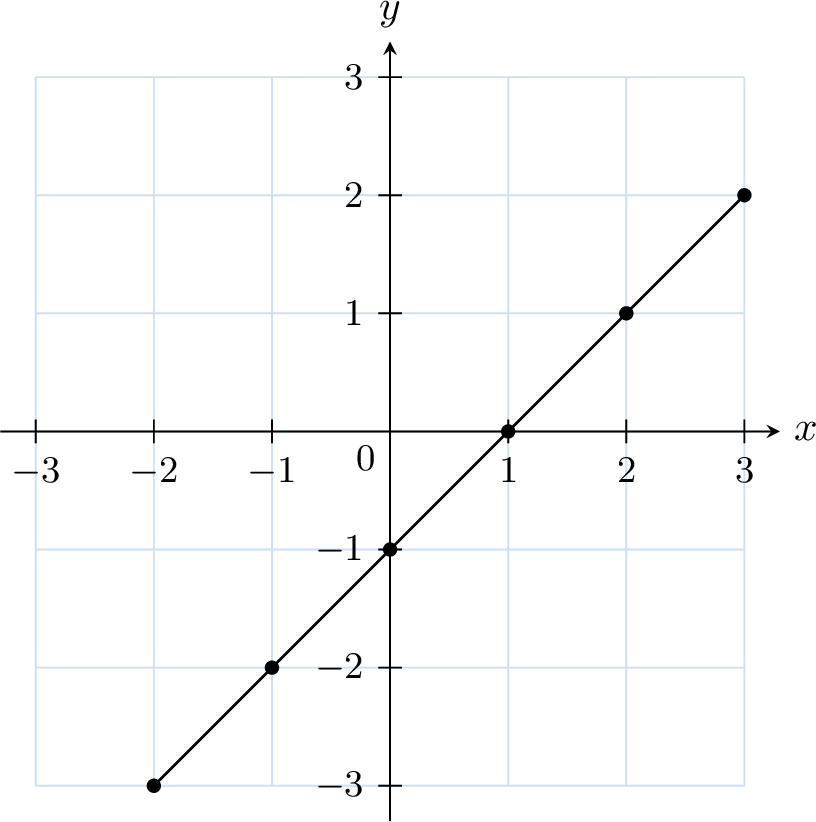
Reading Values and Solving \(f(x)=y\) on a Graph
Method Finding the value \(f(x)\) using a graph
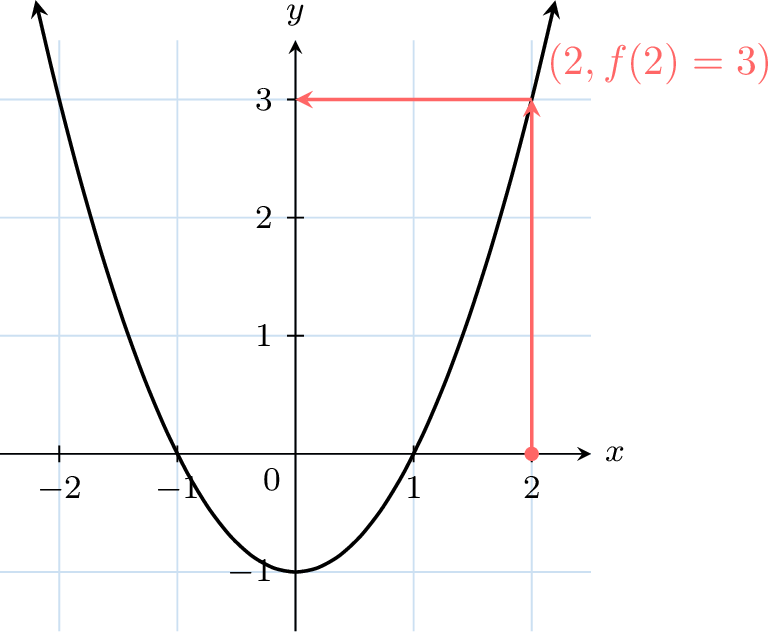
To find \(f(2)\) on a graph, follow these steps:
- Locate the \(x\)-value: Find \(x = 2\) on the \(x\)-axis.
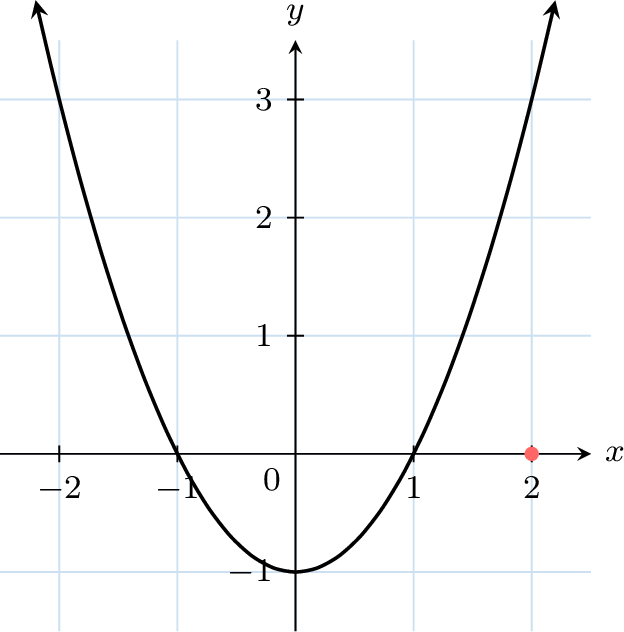
- Move vertically to the curve: From \(x = 2\), draw a vertical line up to the graph.
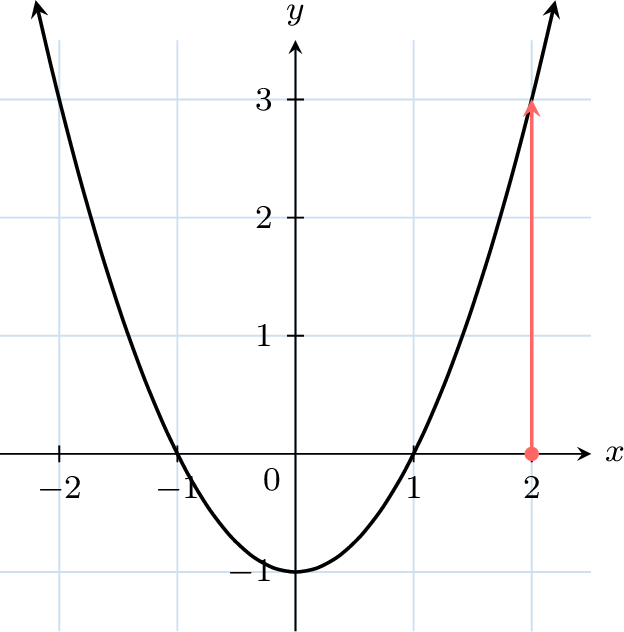
- Read the \(y\)-value: At the intersection with the curve, move horizontally to the \(y\)-axis to find the value \(f(2)\).
Method Finding \(x\) such that \(f(x) = y\) using a graph
To find \(x\) where \(f(x) = 3\) on this graph:
- Locate the \(y\)-value on the \(y\)-axis: Find \(3\) on the \(y\)-axis.
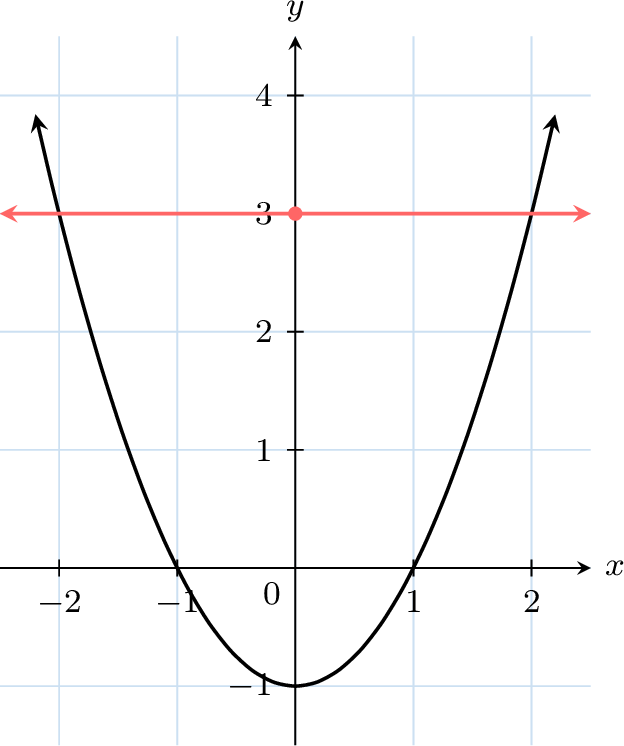
- Draw horizontally to the graph of the function: Draw a horizontal line from \(y = 3\) to the curve.
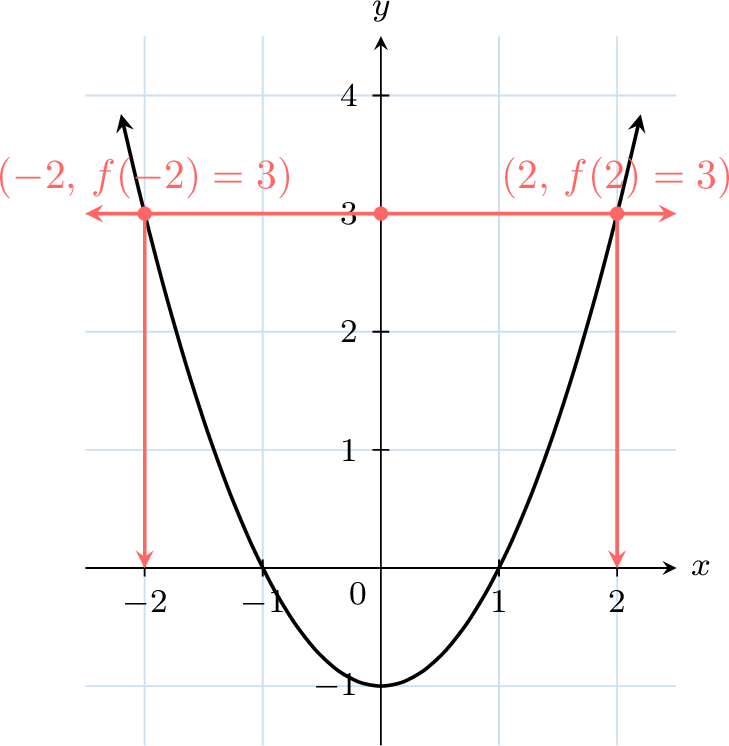
- Read the \(x\)-values: From the intersection points, draw vertical lines down to the \(x\)-axis and read the corresponding \(x\)-values.
Solving \(f(x)=y\) Algebraically
Method Solving \(f(x)=y\) algebraically
To find \(x\) such that \(f(x) = y\):
- Write the equation \(f(x) = y\).
- Solve for \(x\) using algebraic methods (e.g., inverse operations, isolating \(x\)).
Example
Let \(f(x) = 3x + 12\). Find all \(x\) such that \(f(x) = 0\).
We solve the equation:$$\begin{aligned} f(x) &= 0 \\
3x + 12 &= 0 \\
3x + 12 - 12 &= 0 - 12&& \color{gray}\text{(subtract 12 from both sides)} \\
3x &= -12 \\
\frac{3x}{3} &= \frac{-12}{3} &&\color{gray}\text{(divide both sides by 3)} \\
x &= -4\\
\end{aligned}$$So the solution is \(x = -4\).
We can check this by calculating \(f(-4)\):$$f(-4) = 3 \times (-4) + 12 = -12 + 12 = 0$$So \(f(-4) = 0\), as expected.
We can check this by calculating \(f(-4)\):$$f(-4) = 3 \times (-4) + 12 = -12 + 12 = 0$$So \(f(-4) = 0\), as expected.
Domain
Definition Domain
Given a function, the domain is the set of possible \(x\) values for which the function is defined.
Method Finding the Domain
To find the domain of a function, identify the values of \(x\) that make the function undefined (such as division by zero or taking the square root of a negative number), and exclude them from the set of all real numbers.
Example
Find the domain of the function \(f(x)=\sqrt{x}\).
The square root is undefined for negative numbers (\(\sqrt{-1}\) is undefined). So, the domain is \([0,+\infty)\).
Algebra of Functions
Let \(\textcolor{colordef}{f(x)=2x+1}\) and \(\textcolor{colorprop}{g(x)=x^2}\).\(\textcolor{olive}{f(x)+g(x)}\) means that for a given input \(x\), you calculate \(\textcolor{colordef}{f(x)}\) and \(\textcolor{colorprop}{g(x)}\) separately, then add the results.This is illustrated by the function machine below: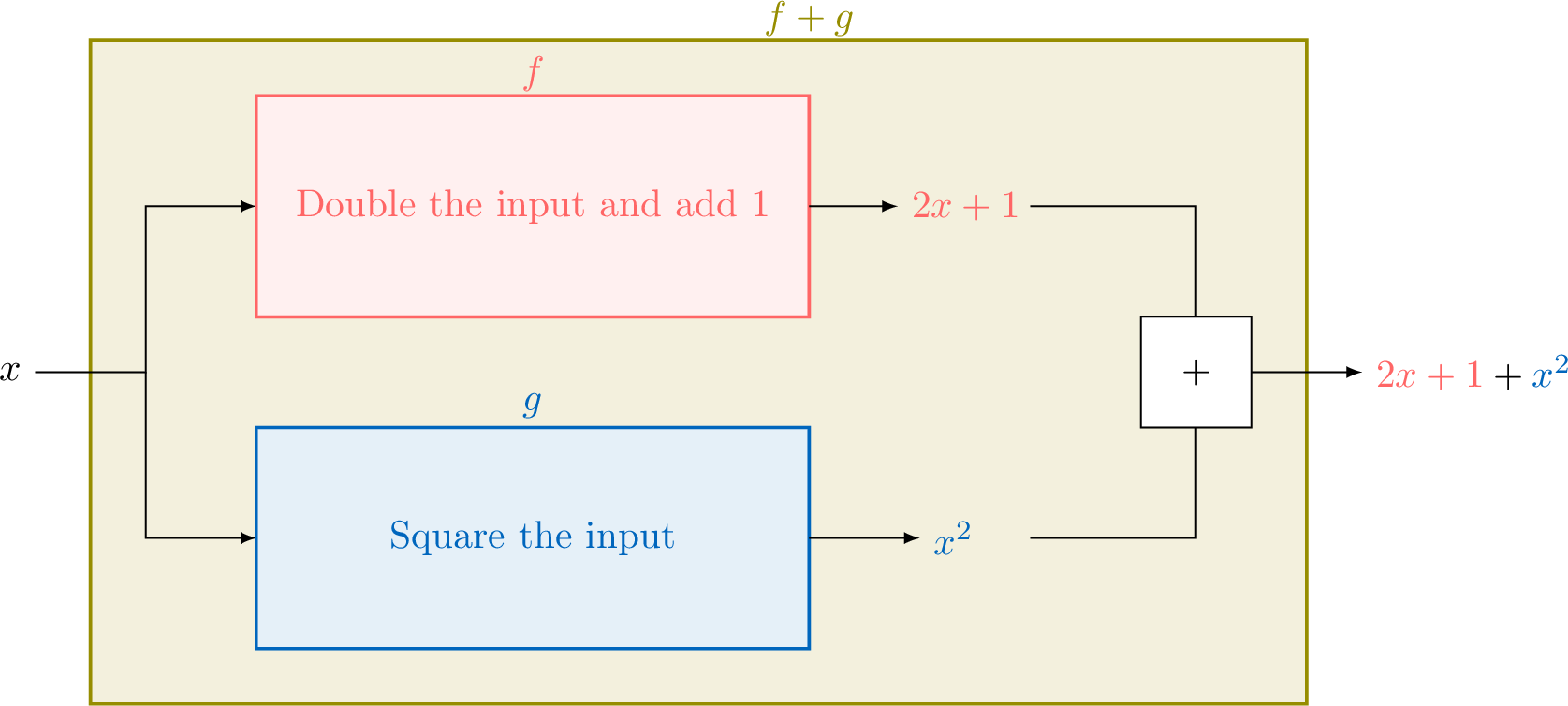

Definition Operations on Functions
Given functions \(f\) and \(g\):
- The sum of functions is \(x\mapsto f(x) + g(x)\).
- The product of functions is \(x\mapsto f(x) \times g(x)\).
Example
Let \(f(x)=2x+1\) and \(g(x)=x^4-1\). Find \(f(x)+g(x)\).
\(\begin{aligned} f(x) + g(x) &=(2x+1) + (x^4-1) \\ &= x^4 + 2x\end{aligned}\)
Composition
Let \(\textcolor{colordef}{f(x)=x^2}\) and \(\textcolor{colorprop}{g(x)=2x+1}\).\(\textcolor{olive}{f(g(x))}\) means that you first apply \(g\) to \(x\), and then apply \(f\) to the result. In other words, \(x\) goes through \(g\) (becomes \(2x+1\)), and then \(f\) (becomes \((2x+1)^2\)).This is illustrated by the function machine below: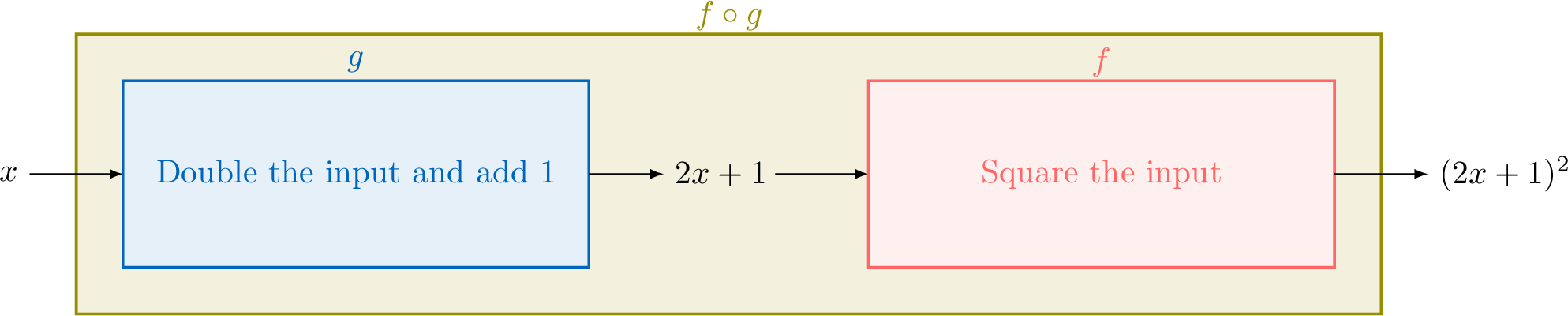

Definition Composition of Functions
Given two functions \(f\) and \(g\), the composition of functions of \(f\) and \(g\) is \(x\mapsto f(g(x))\).
This means you first apply \(g\) to \(x\), then apply \(f\) to the result.
This means you first apply \(g\) to \(x\), then apply \(f\) to the result.
Example
Let \(f(x)=x^2\) and \(g(x)=2x+1\).
- Find \(f(g(x))\).
- Find \(g(f(x))\).
- Is \(f(g(x)) = g(f(x))\)?
- \(\begin{aligned}[t] f(g(x)) &= f(g(x)) \\ &= f(2x+1) \\ &= (2x+1)^2 \\ &= 4x^2 + 4x + 1 \end{aligned}\)
- \(\begin{aligned}[t] g(f(x)) &= g(f(x)) \\ &= g(x^2) \\ &= 2x^2 + 1 \end{aligned}\)
- So \(f(g(x)) \neq g(f(x))\).
Inverse Function
The operations of \(+\) and \(-\), and \(\times\) and \(\div\), are called inverse operations because one “undoes” the other.
In a similar way, some functions have inverse functions that “undo” the effect of the original function.
Definition of an inverse function: If a function \(f\) takes \(x\) and produces \(f(x)\), then the inverse function \(f^{-1}\) reverses this process: it takes \(f(x)\) and returns \(x\).That is, applying \(f\) and then \(f^{-1}\) brings you back to where you started, and vice versa.
In a similar way, some functions have inverse functions that “undo” the effect of the original function.
Definition of an inverse function: If a function \(f\) takes \(x\) and produces \(f(x)\), then the inverse function \(f^{-1}\) reverses this process: it takes \(f(x)\) and returns \(x\).That is, applying \(f\) and then \(f^{-1}\) brings you back to where you started, and vice versa.
Definition Inverse Function
A function \(f^{-1}\) is called the inverse function of \(f\) if:$$f^{-1}(f(x)) = x \quad \text{and} \quad f(f^{-1}(x)) = x.$$
When does an inverse exist?
A function \(f\) has an inverse function \(f^{-1}\) only if, for every value of \(f(x)\), there is exactly \emph{one} value of \(x\) that produces it (i.e., \(f\) is one-to-one).
A function \(f\) has an inverse function \(f^{-1}\) only if, for every value of \(f(x)\), there is exactly \emph{one} value of \(x\) that produces it (i.e., \(f\) is one-to-one).
Method Finding the Inverse Function
To find the inverse of \(f(x)\):
- Set \(y = f(x)\).
- Solve the equation for \(x\) in terms of \(y\).
- Replace \(y\) with \(x\); the result is \(f^{-1}(x)\).
Example
Find the inverse of \(f(x) = 4x - 8\).
Set \(y = 4x - 8\).$$\begin{aligned}y &= 4x - 8 \\
y + 8 &= 4x \\
x &= \frac{y + 8}{4}\end{aligned}$$So, the inverse function is \(f^{-1}(x) = \frac{x + 8}{4}\).
Proposition Symmetry of the Graphs of a Function and Its Inverse
The graph of a function \(f\) and its inverse \(f^{-1}\) are symmetric with respect to the line \(y = x\) (the first bisector).