Function Transformations
Function transformations allow us to modify the graph of a parent function to create new functions without starting from scratch.
By applying translations, dilations, and reflections, we can shift, stretch, compress, or flip the graph in various ways. These transformations are essential in understanding how changes to a function's equation affect its graphical representation and are widely used in modeling real-world phenomena. In this chapter, we will explore vertical and horizontal translations, dilations, and reflections, using examples and graphical illustrations to demonstrate each concept.
By applying translations, dilations, and reflections, we can shift, stretch, compress, or flip the graph in various ways. These transformations are essential in understanding how changes to a function's equation affect its graphical representation and are widely used in modeling real-world phenomena. In this chapter, we will explore vertical and horizontal translations, dilations, and reflections, using examples and graphical illustrations to demonstrate each concept.
Translation
Proposition Vertical Translation by Adding a Constant
The graph of \(x\mapsto f(x)+a\) is obtained by translating the graph of \(x\mapsto f(x)\) by the vector \(\begin{pmatrix}0 \\ a\end{pmatrix}\) 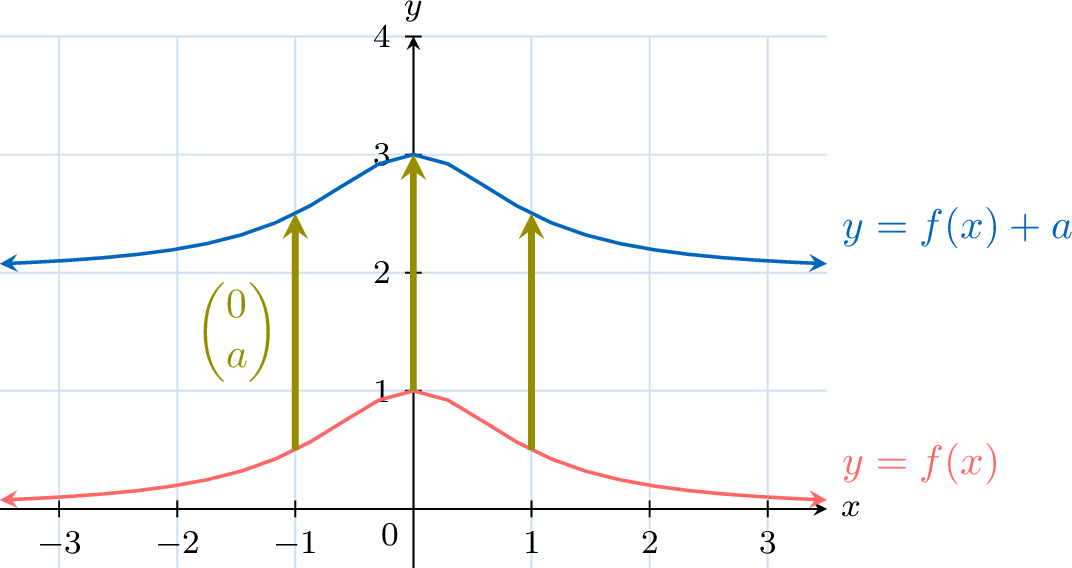

Dilation
Proposition Dilation
The graph of \(x\mapsto k f(x)\) is obtained by dilating the graph of \(x\mapsto f(x)\) by the factor \(k\). 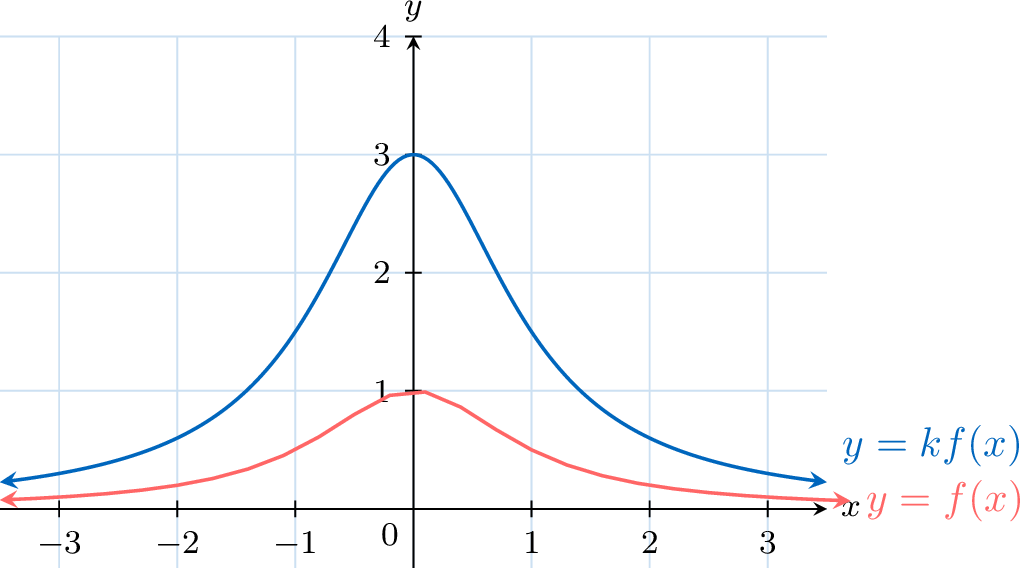

Reflection
Proposition Reflection over the x-axis
The graph of \(x\mapsto -f(x)\) is obtained by reflecting the graph of \(x\mapsto f(x)\) over the x-axis. 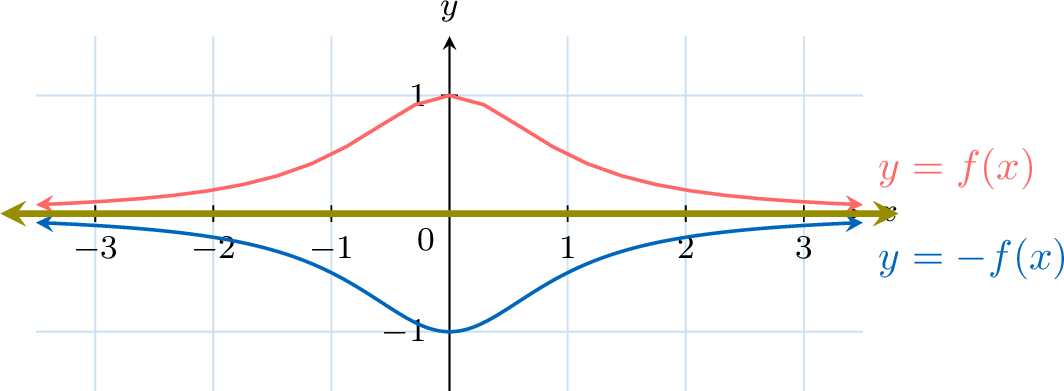

Proposition Reflection over the y-axis
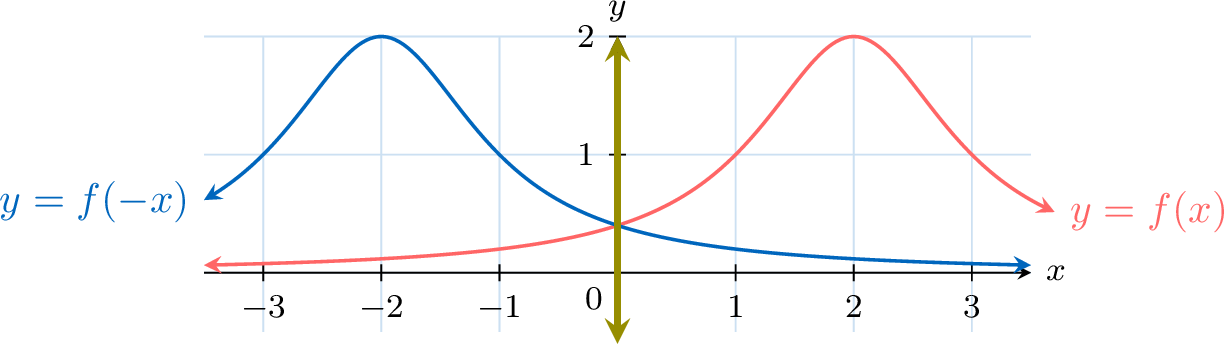
The graph of \(x\mapsto f(-x)\) is obtained by reflecting the graph of \(x\mapsto f(x)\) over the y-axis.