Logarithms

In previous chapters, we explored exponential functions of the form $f(x) = 10^x$. This chapter introduces the inverse of these functions: logarithms. Logarithms are essential for solving equations where the unknown is in the exponent, and they have wide applications in science, engineering, and finance, such as measuring pH levels, earthquake magnitudes, and sound intensity.

Definition

Definition Logarithm

The logarithm of a number $y$ (where $y > 0$) is the exponent to which 10 must be raised to obtain $y$. It is denoted as:$$\log y = x \quad \Leftrightarrow \quad 10^x = y$$

Proposition Inverse Properties of Logarithms

For any $x > 0$:

$10^{\log x} = x$
$\log (10^x) = x$

These properties reflect that the exponential function $10^x$ and the logarithm function $\log x$ are inverses of each other.

Example

Evaluate $\log 100$.

Answer

$\begin{aligned}[t]\log(100) &= \log\left(10^{2}\right) \\&=2\\\end{aligned}$

Laws of Logarithms

Proposition Laws of Logarithms

For positive real numbers $x$, $y$:

Product Rule: $\log (xy) = \log x + \log y$
Quotient Rule: $\log \left(\dfrac{x}{y}\right) = \log x - \log y$
Power Rule: $\log (x^k) = k \log x$

Proof

$$\begin{aligned}\log(xy) &= \log(10^{\log x} \times 10^{\log y}) \\ &= \log(10^{\log x + \log y}) \\ &= \log x+ \log y \\ \\ \log\left(\frac{x}{y}\right) &= \log\left(\frac{10^{\log x}}{10^{\log y}}\right) \\ &= \log(10^{\log x - \log y}) \\ &= \log x - \log y \\ \\ \log(x^k) &= \log\left(\left(10^{\log x}\right)^k\right) \\ &= \log(10^{k \log x}) \\ &= k \log x\\ \end{aligned} $$

Example

Write as a single logarithm $\log (5)+\log (3)$.

Answer

$\begin{aligned}[t]\log (5)+\log (3) &= \log (5\times 3) \\&= \log 15\\\end{aligned}$

Using Logarithms to Solve Exponential Equations

Method Solving Exponential Equations Using Logarithms

To solve an exponential equation of the form $a^x = b$ (where $a > 0$, $a \neq 1$, $b > 0$):

Take the logarithm (base 10) of both sides: $\log(a^x) = \log b$
Apply the power rule: $x \log a = \log b$
Solve for $x$: $x = \frac{\log b}{\log a}$

Example

Solve $2^x = 7$.

Answer

$$\begin{aligned}2^x &= 7 \\ \log(2^x) &= \log 7 &&\text{(taking log of both sides)}\\ x \log 2 &= \log 7 &&\text{(power rule)}\\ x &= \frac{\log 7}{\log 2} &&\text{(dividing both sides by } \log 2\text{)}\\ x &\approx 2.807 &&\text{(using calculator)}\\ \end{aligned}$$

Applications of Logarithms

Logarithms are used to describe quantities that vary over many orders of magnitude. Some important examples in science include:

pH scale in chemistry: $\text{pH} = -\log_{10} [H^+]$
(where $[H^+]$ is the hydrogen ion concentration in moles per litre)
Richter scale for earthquakes: $\text{Magnitude} = \log_{10}\left(\dfrac{I}{I_0}\right)$
(where $I$ is the intensity of the earthquake, $I_0$ is a reference intensity)
Decibel (dB) scale for sound: $L = 10 \log_{10}\left(\dfrac{P}{P_0}\right)$
(where $P$ is the power/intensity measured, $P_0$ is a reference level)

Example

The pH of a solution is $3.2$. Find the hydrogen ion concentration $[H^+]$.

Answer

We know:$$\begin{aligned}\text{pH} &= -\log_{10}[H^+] \\ 3.2 &= -\log_{10}[H^+] &&\text{(substituting the value)}\\ -3.2 &= \log_{10}[H^+] &&\text{(multiplying both sides by $-1$)}\\ 10^{-3.2} &= 10^{\log_{10}[H^+]} &&\text{(exponentiating both sides)}\\ [H^+] &= 10^{-3.2} \\ [H^+] &\approx 6.31 \times 10^{-4}\ \text{mol/L} &&\text{(using calculator)}\end{aligned}$$

Graphs of Logarithmic Functions

Definition Logarithmic Function

The logarithmic function is $x\mapsto \log x$ with domain $(0,+\infty)$.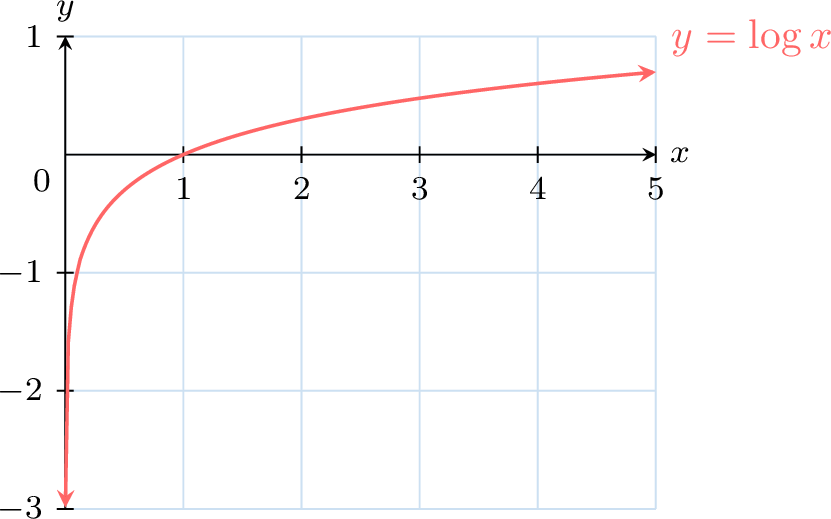

Proposition Graph Properties

The graph of $y = \log x$ is the inverse of $y = 10^x$. It has a vertical asymptote at $x=0$, passes through (1,0), and is increasing.