Trigonometric Functions
Trigonometric functions are real-valued functions that relate the measure of an angle in a right triangle to the ratios of two of its sides. They play a fundamental role in geometry and are widely used in many scientific fields, such as navigation, mechanics, astronomy, geodesy, and more. Trigonometric functions are also among the simplest examples of periodic functions, making them essential for modeling periodic phenomena (such as waves) and for applications like Fourier analysis.
Definitions
et \(M(\cos x, \sin x)\) be the point on the unit circle corresponding to an angle \(x\) (in radians).
See for example: https://www.geogebra.org/m/j7w29vj4.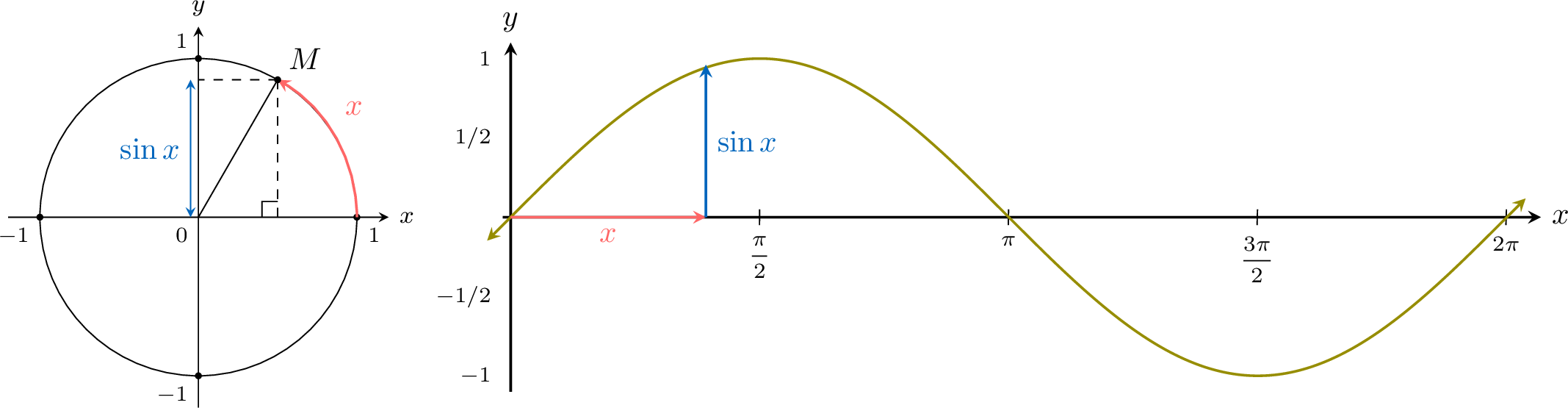
- The angle \(x\) on the unit circle corresponds to the input for the sine function.
- The \(y\)-coordinate of point \(M\) on the unit circle, \(\sin x\), gives the output of the sine function.
See for example: https://www.geogebra.org/m/j7w29vj4.

Definition Sine function
The sine function, denoted \(\sin\), is defined by \(x\mapsto \sin(x)\), where \(x\) is interpreted as an angle in radians.
Example
Complete the following table with the values of the sine function at key angles:
| \(x\) | 0 | \(\dfrac{\pi}{6}\) | \(\dfrac{\pi}{4}\) | \(\dfrac{\pi}{3}\) | \(\dfrac{\pi}{2}\) | \(\dfrac{2 \pi}{3}\) | \(\dfrac{3 \pi}{4}\) | \(\dfrac{5 \pi}{6}\) | \(\pi\) |
| \(\sin (x)\) |
| \(x\) | 0 | \(\dfrac{\pi}{6}\) | \(\dfrac{\pi}{4}\) | \(\dfrac{\pi}{3}\) | \(\dfrac{\pi}{2}\) | \(\dfrac{2 \pi}{3}\) | \(\dfrac{3 \pi}{4}\) | \(\dfrac{5 \pi}{6}\) | \(\pi\) |
| \(\sin (x)\) | 0 | \(\dfrac{1}{2}\) | \(\dfrac{1}{\sqrt{2}}\) | \(\dfrac{\sqrt{3}}{2}\) | 1 | \(\dfrac{\sqrt{3}}{2}\) | \(\dfrac{1}{\sqrt{2}}\) | \(\dfrac{1}{2}\) | \(0\) |
If we instead project the values of \(\cos x\) from the unit circle onto a graph, we obtain the graph of the cosine function \(x \mapsto \cos x\).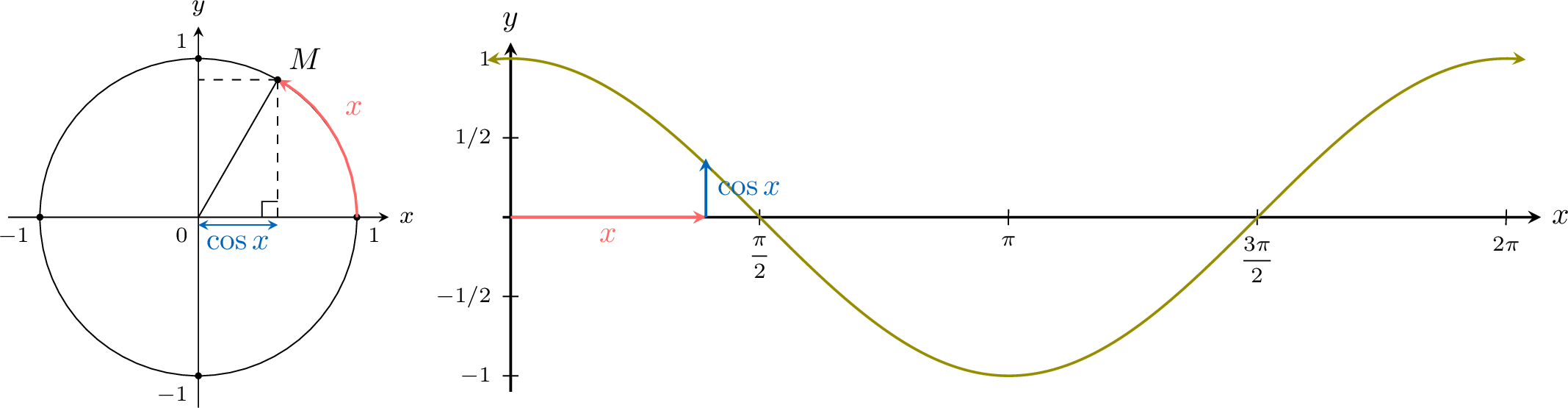

Definition Cosine Function
The cosine function, denoted \(\cos\), is defined by \(x\mapsto\cos(x)\), where \(x\) is interpreted as an angle in radians.
Example
Complete the following table with the values of the cosine function at key angles:
| \(x\) | 0 | \(\dfrac{\pi}{6}\) | \(\dfrac{\pi}{4}\) | \(\dfrac{\pi}{3}\) | \(\dfrac{\pi}{2}\) | \(\dfrac{2 \pi}{3}\) | \(\dfrac{3 \pi}{4}\) | \(\dfrac{5 \pi}{6}\) | \(\pi\) |
| \(\cos (x)\) |
| \(x\) | 0 | \(\dfrac{\pi}{6}\) | \(\dfrac{\pi}{4}\) | \(\dfrac{\pi}{3}\) | \(\dfrac{\pi}{2}\) | \(\dfrac{2 \pi}{3}\) | \(\dfrac{3 \pi}{4}\) | \(\dfrac{5 \pi}{6}\) | \(\pi\) |
| \(\cos (x)\) | 1 | \(\dfrac{\sqrt{3}}{2}\) | \(\dfrac{1}{\sqrt{2}}\) | \(\dfrac{1}{2}\) | \(0\) | \(-\dfrac{1}{2}\) | \(-\dfrac{1}{\sqrt{2}} \) | \(-\dfrac{\sqrt{3}}{2}\) | \(-1\) |