Quadratic Functions
Definition
Definition Quadratic Function
A quadratic function is \(x \mapsto ax^2 + bx + c\) where \(a \neq 0\).
Example
For \(f(x) = x^2 - 3x + 1\), evaluate \(f(2)\).
\(\begin{aligned}[t]f(2) &= (2)^2 - 3(2) + 1 \\&= 4 - 6 + 1 \\&= -1\end{aligned}\)
Graph
The parabola is one of the conic sections, which are the group of curves obtained by intersecting a cone with a plane. A parabola is produced by intersecting the cone with a plane parallel to its generating line. By intersecting the cone at other angles, we can produce circles, hyperbolas, and ellipses.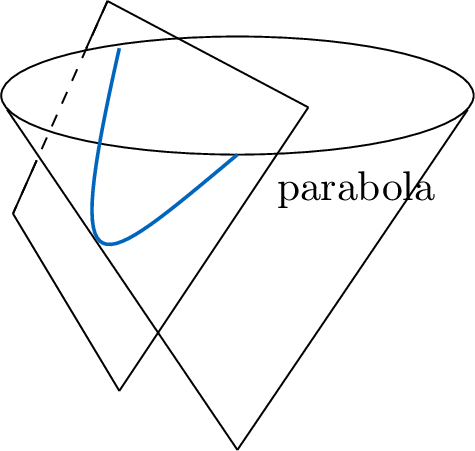

Definition Parabola
Given a quadratic function \(x \mapsto ax^2 + bx + c\) where \(a \neq 0\), its graph is called a parabola.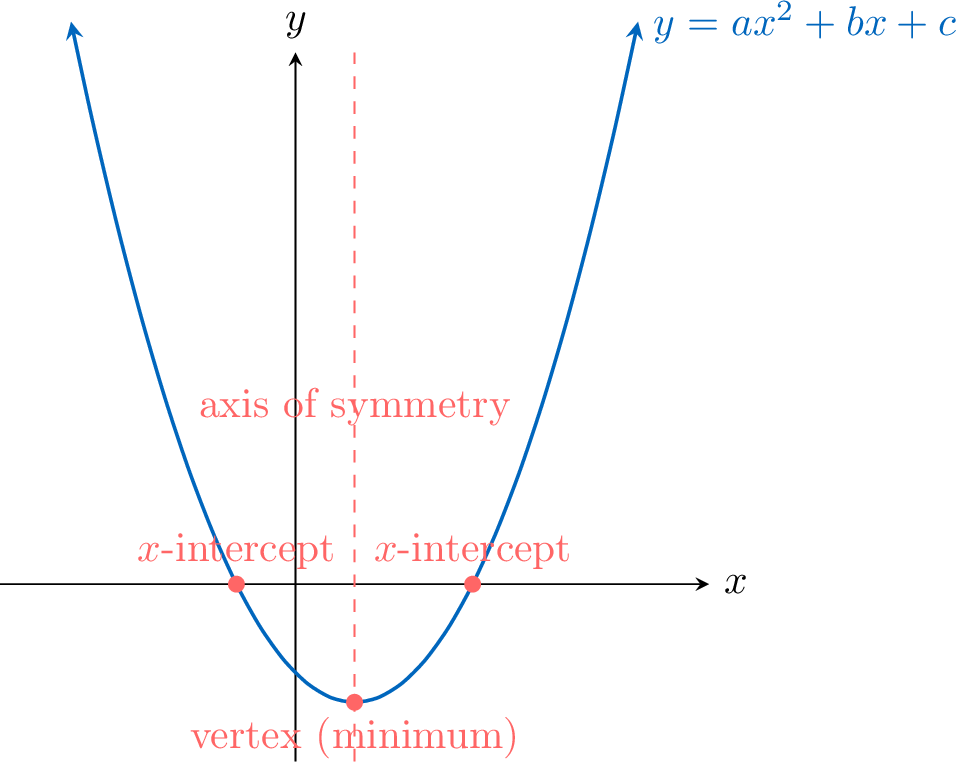

Example
Sketch the graph of \(x \mapsto x^2 - x - 1\).
A table of values is
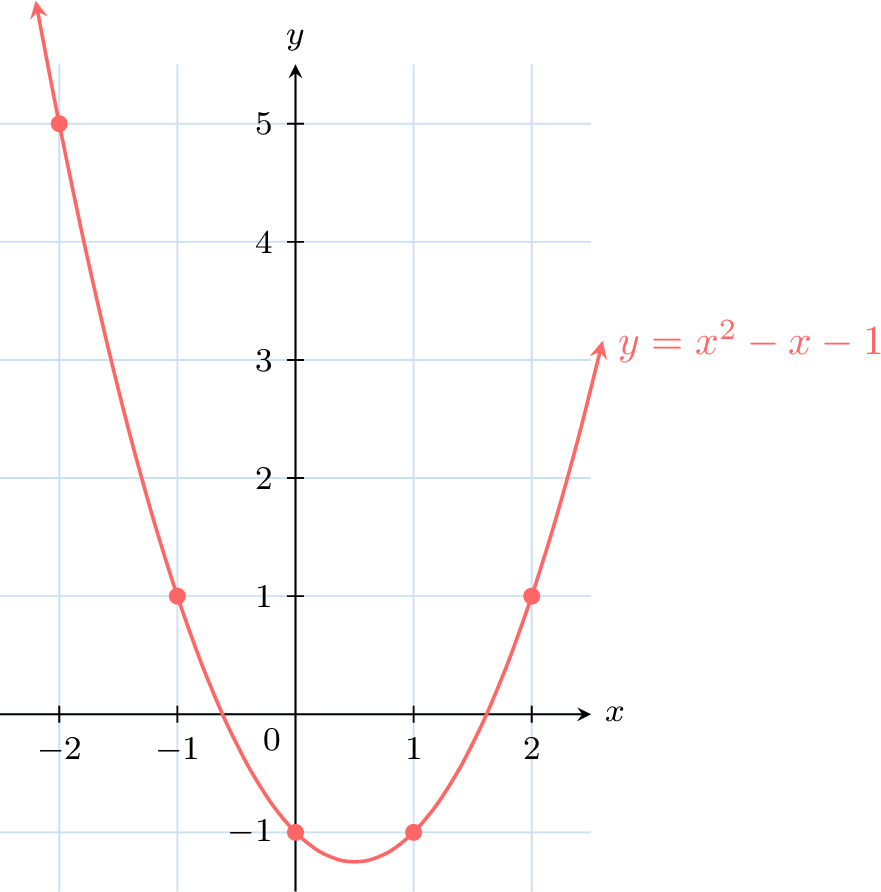
| \(x\) | \(-2\) | \(-1\) | 0 | 1 | 2 |
| \(y\) | 5 | 1 | \(-1\) | \(-1\) | 1 |

To understand the concavity based on the sign of \(a\), use the GeoGebra animation at https://www.geogebra.org/m/gn3c2sqe.
Proposition Concavity
For any quadratic function \(x \mapsto ax^2 + bx + c\), \(a \neq 0\):
- If \(a > 0\), the graph is concave up:
 .
. - If \(a < 0\), the graph is concave down:
 .
.
Solving \(f(x) \equal y\)
Method Solving \(f(x) \equal y\)
When solving for a value of \(f(x) = y\), we obtain a quadratic equation in \(x\). Since it is quadratic, there may be 0, 1, or 2 real solutions for \(x\).
Example
For \(f(x) = 2x^2 - 5x + 2\), find the \(x\)-intercepts of the function.
Set \(f(x) = 0\): \(2x^2 - 5x + 2 = 0\), with \(a=2\), \(b=-5\), \(c=2\).
- \(\begin{aligned}[t]\Delta &= b^2 - 4ac \\&= (-5)^2 - 4(2)(2) \\&= 25 - 16 \\&= 9\end{aligned}\)
- As \(\Delta > 0\), there are 2 distinct roots.
- \(\begin{aligned}[t]x &= \frac{-b - \sqrt{\Delta}}{2a} &\text{ or } x &= \frac{-b + \sqrt{\Delta}}{2a} \\x &= \frac{-(-5) - \sqrt{9}}{2 \cdot 2} &\text{ or } x &= \frac{-(-5) + \sqrt{9}}{2 \cdot 2} \\x &= \frac{5 - 3}{4} &\text{ or } x &= \frac{5 + 3}{4} \\x &= \frac{2}{4} &\text{ or } x &= \frac{8}{4} \\x &= \frac{1}{2} &\text{ or } x &= 2\end{aligned}\)
Proposition Relative position between the graph and the \(x\)-axis
For any quadratic function \(x \mapsto ax^2 + bx + c\) and the discriminant \(\Delta = b^2 - 4ac\):
- If \(\Delta > 0\), then the graph intersects the \(x\)-axis twice.
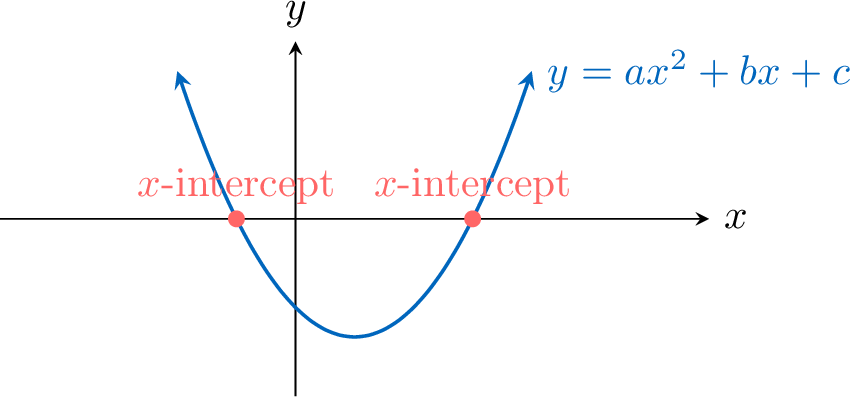
- If \(\Delta = 0\), then the graph touches the \(x\)-axis at one point.
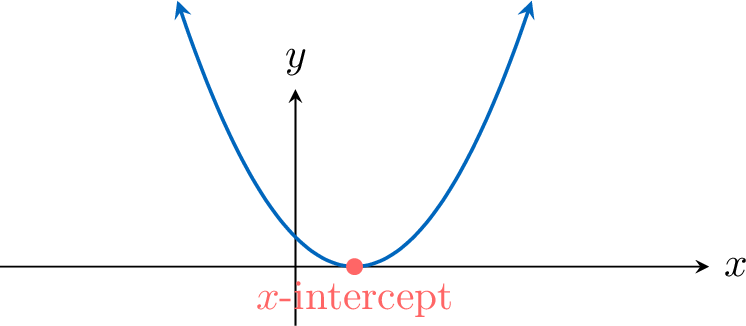
- If \(\Delta < 0\), then the graph does not intersect the \(x\)-axis.