Sequences
Numerical Sequence
Definition Numerical Sequence
A numerical sequence, \((u_n)\) is an ordered list of numbers \((u_0,\,u_1,\,u_2,\dots)\) defined by a rule.
The number \(u_n\) is called the \(n\)th term of the sequence.
The number \(u_n\) is called the \(n\)th term of the sequence.
Example
What is \(u_4\) of this sequence?
| \(n\) | 0 | 1 | 2 | 3 | 4 | 5 | \(\dots\) |
| \(u_n\) | 3 | 5 | 7 | 9 | 11 | 13 | \(\dots\) |
\(u_4 = 11\).
Definition Using a Recursive Rule
Let’s consider a sequence where the first term is \(2\), and each term is obtained by adding \(3\) to the previous term. The terms are: 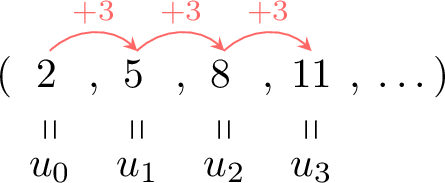
We observe: 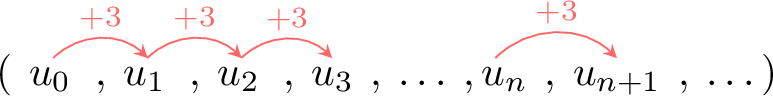

- \(5 = 2\textcolor{colordef}{+3} \longrightarrow u_1 = u_0\textcolor{colordef}{+3} \longrightarrow u_{0+1} = u_0+3\)
- \(8 = 5\textcolor{colordef}{+3} \longrightarrow u_2 = u_1\textcolor{colordef}{+3} \longrightarrow u_{1+1} = u_1+3\)
- \(11 = 8\textcolor{colordef}{+3} \longrightarrow u_3 = u_2\textcolor{colordef}{+3} \longrightarrow u_{2+1} = u_2+3\)
- \(\vdots\)
- So the rule is \(u_{n+1} = u_n + 3\)
Definition Recursive Rule
A sequence can be defined by:
- the first term (starting number): \(u_0\)
- a recursive rule that tells how to obtain each term from the previous one:
\(u_{n+1}=\) expression in \(u_n\)
Example
Write the recursive rule when each term is obtained by adding \(2\) to the previous term.
$$u_{n+1}=u_n+2$$
Definition Using an Explicit Rule
Definition Explicit Rule
A sequence can also be defined by an explicit rule (or explicit formula), which gives a direct formula for the \(n\)th term in terms of \(n\):$$u_n = \text{expression in } n$$
Example
Consider the sequence defined by the explicit formula: \(u_n = 3n + 2\).
Write the first five terms of this sequence.
Write the first five terms of this sequence.
- For \(n=0\): $$ \begin{aligned}[t] u_0 &= 3 \times 0 + 2 \\ &= 0 + 2 \\ &= 2 \end{aligned} $$
- For \(n=1\): $$ \begin{aligned}[t] u_1 &= 3 \times 1 + 2 \\ &= 3 + 2 \\ &= 5 \end{aligned} $$
- For \(n=2\): $$ \begin{aligned}[t] u_2 &= 3 \times 2 + 2 \\ &= 6 + 2 \\ &= 8 \end{aligned} $$
- For \(n=3\): $$ \begin{aligned}[t] u_3 &= 3 \times 3 + 2 \\ &= 9 + 2 \\ &= 11 \end{aligned} $$
- For \(n=4\): $$ \begin{aligned}[t] u_4 &= 3 \times 4 + 2 \\ &= 12 + 2 \\ &= 14 \end{aligned} $$
Arithmetic Sequences
Definition Arithmetic Sequence
An arithmetic sequence is a sequence where the difference between consecutive terms is constant. This constant is called the common difference and is denoted by \(d\). 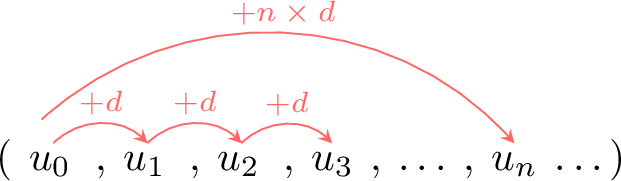
- The recursive rule is: \(u_{n+1} = u_n + d\)
- The explicit formula is: \(u_n = u_0 + n d\)
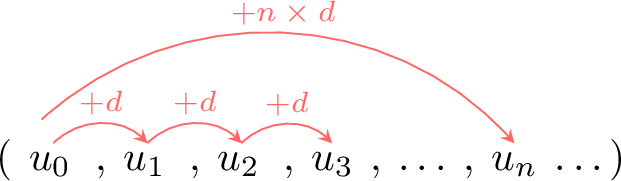
Example
Determine if the sequence \((2, 5, 8, 11, 14, \dots)\) is arithmetic and find the common difference \(d\) if it is.
Since the difference is constant and equal to \(3\), the sequence is arithmetic with \(d = 3\).
Geometric Sequences
Definition Geometric Sequence
An geometric sequence is a sequence where the ratio between consecutive terms is constant. This constant is called the common ratio and is denoted by \(r\). 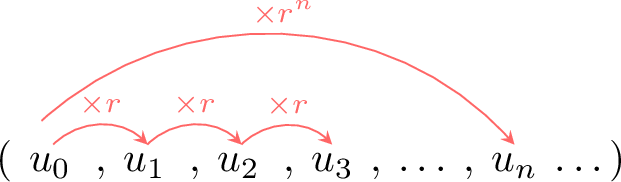
- The recursive rule is: \(u_{n+1} = u_n \times r\)
- The explicit formula is: \(u_n = u_0 \times r^n\)
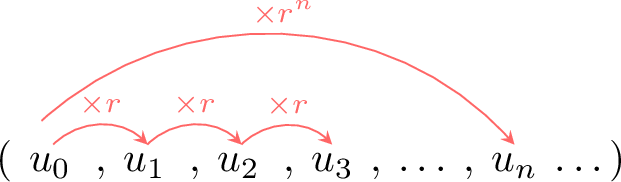
Example
Determine if the sequence \((2, 6, 18, 54, 162, \dots)\) is geometric and find the common ratio \(r\) if it is.
Since the ratio is constant and equal to \(3\), the sequence is geometric with \(r = 3\).
Series
Definition Series
A series is the sum of the terms of a sequence.$$\begin{aligned}S_n &= u_0 + u_1 + u_2 + \ldots + u_n\\
&=\sum_{i=0}^n u_i \\
\end{aligned}$$
Sum of an Arithmetic Sequence
We want to calculate$$S_{19} = \overbrace{5 + 10 + 15 + \ldots + 90 + 95 + 100}^{20~\text{terms}}$$The first term is \(u_0 = 5\) and the last term is \(u_{19} = 100\). However, we can also write:$$\begin{aligned}&&S_{19}&= & 5 &+& 10 &+& 15 &+& \ldots &+& 90 &+& 95 &+& 100 \\
+\,\,\,&&S_{19}&= & 100 &+& 95 &+& 90 &+& \ldots &+& 15 &+& 10 &+& 5 && \text{(reversing the terms)}\\
\hline&&2S_{19}&= & 105 &+& 105 &+& 105 &+& \ldots &+& 105 &+& 105 &+& 105 && \text{(adding)}\\
&&2S_{19}&= & 20 \times 105 &&&&&&&&&&&&&& \text{(20 times the same term)}\\
\end{aligned}$$So$$S_{19} = \dfrac{20}{2} \times 105 = 1050$$
Proposition Sum of an Arithmetic Sequence
The sum of an arithmetic sequence is$$S_n = \frac{n+1}{2}\left(u_0 + u_n\right)$$
Sum of an Geometric Sequence
Proposition Sum of a Geometric Sequence
The sum of a geometric sequence is$$S_n = u_0 \cdot \frac{1 - r^{n+1}}{1 - r}$$where \(r\) is the common ratio.