Vectors
Definition
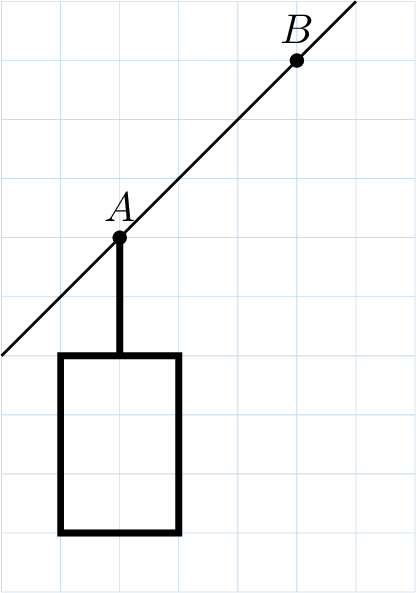
Moving a figure by translation means sliding the figure without rotating it. To describe this movement, we use an arrow \(\vec{u}\) called a vector. To translate all points by a vector, we can use: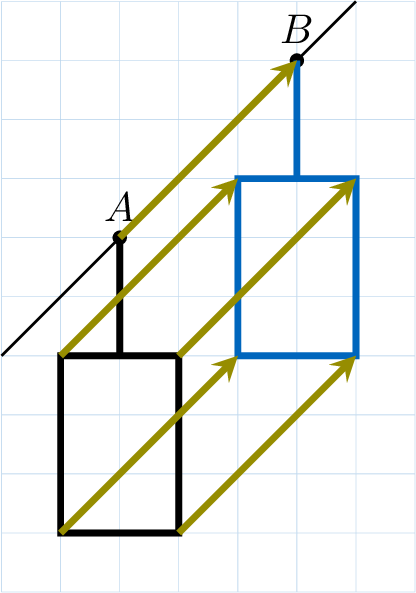
- the length of the arrow (magnitude) and the direction (orientation and sense).
- the \(x\)-step and \(y\)-step of the vector (how many units to the right/left and up/down).

Definition Vector
A vector \(\Vect{u}\) can be defined:
- Geometrically, as having a direction (including orientation and sense) and a magnitude (length).
- Algebraically, as an ordered pair of components \(\begin{pmatrix} \textcolor{colordef}{x-\text{step}}\\\textcolor{colorprop}{y-\text{step}}\end{pmatrix}\).
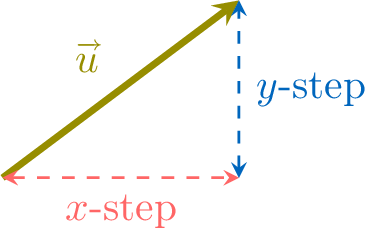
- The \(x\)-step is positive if the movement is to the right and negative if to the left.
- The \(y\)-step is positive if the movement is upwards and negative if downwards.
Example
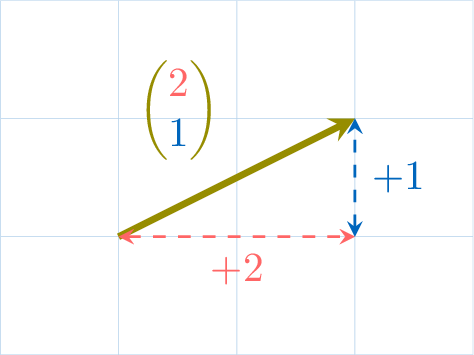 \(\quad\quad\quad\)
\(\quad\quad\quad\) 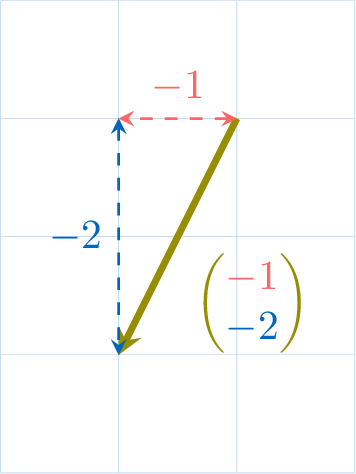
Two Point Notation
Definition Two Point Notation
The vector from \(A\) to \(B\) can be written as: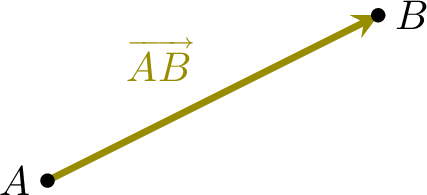
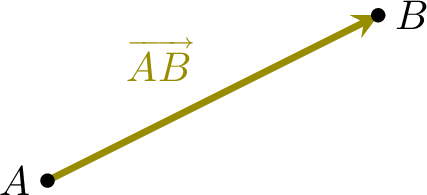
Proposition Components of \(\Vect{AB}\)
Let \(A(x_A,\,y_A)\) and \(B(x_B,\,y_B)\) be two points. The components of the vector \(\Vect{AB}\) are:$$\Vect{AB} = \begin{pmatrix}x_B - x_A \\
y_B - y_A\end{pmatrix}$$
Equality between Vectors
Two vectors are said to be equal if they represent the same translation.
Definition Geometric Equality of Vectors
Two vectors are equal if they have: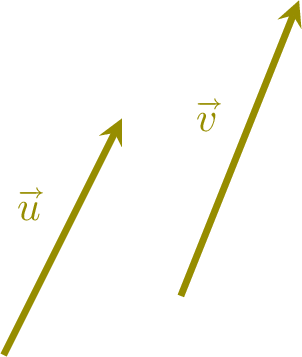
\(\textcolor{olive}{\Vect{u}} = \textcolor{olive}{\Vect{v}}\)
- the same direction (parallel lines),
- the same sense (same orientation),
- and the same magnitude (same length).
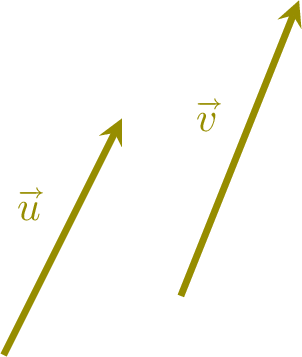
\(\textcolor{olive}{\Vect{u}} = \textcolor{olive}{\Vect{v}}\)
Definition Algebraic Equality of Vectors
Two vectors \(\begin{pmatrix}x\\y\end{pmatrix}\) and \(\begin{pmatrix}x'\\y'\end{pmatrix}\) are equal if \(x = x'\) and \(y = y'\).
Proposition Parallelogram criterion
Two vectors \(\Vect{AB}\) and \(\Vect{CD}\) are equal if and only if \(ABDC\) is a parallelogram (possibly flattened).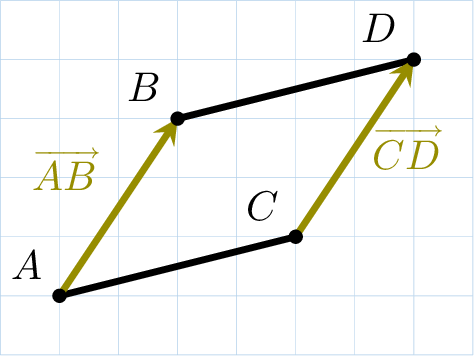

Addition
Suppose we translate the point \(A\) to \(B\), then we translate the point \(B\) to \(C\).
This is equivalent to translating the point \(A\) directly to \(C\).
In vector terms, this is written as the sum: \(\Vect{AB}+\Vect{BC}=\Vect{AC}\), where the \(+\) symbol can be read as “followed by.”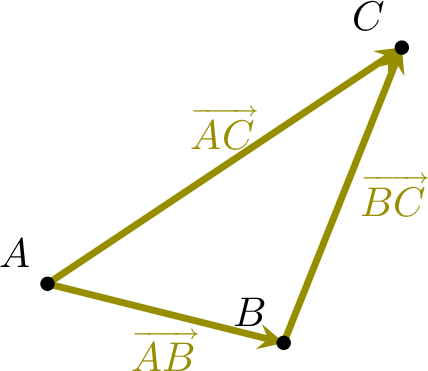
This is equivalent to translating the point \(A\) directly to \(C\).
In vector terms, this is written as the sum: \(\Vect{AB}+\Vect{BC}=\Vect{AC}\), where the \(+\) symbol can be read as “followed by.”

Definition Vector Addition
The sum of two vectors \(\vec{u}\) and \(\vec{v}\), written \(\vec{u} + \vec{v}\), is the vector corresponding to performing the translation by \(\vec{u}\) followed by the translation by \(\vec{v}\).
Definition Algebraic Vector Addition
$$\begin{pmatrix}x\\
y\end{pmatrix}+\begin{pmatrix}x'\\
y'\end{pmatrix}=\begin{pmatrix}x+x'\\
y +y' \\
\end{pmatrix}$$
Proposition Chasles' Relation
For any points \(A\), \(B\), and \(C\),$$\Vect{AB} + \Vect{BC} = \Vect{AC}$$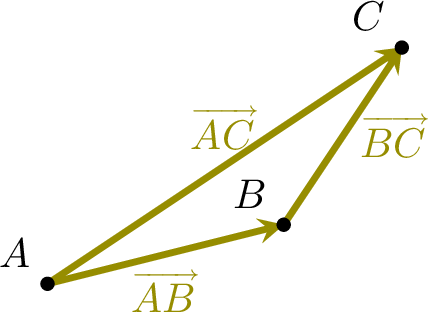

Having defined vector addition, we can now state that:
Definition Null Vector
The vector associated with the translation that transforms any point into itself is the null vector, denoted \(\Vect{0}\).$$\Vect{v} + \Vect{0} = \Vect{0} + \Vect{v} = \Vect{v}$$
For any point \(A\):$$\Vect{AA} = \Vect{0}$$
Subtraction
Suppose we translate the point \(A\) to \(B\), then we translate the point \(B\) back to \(A\).
This is equivalent to staying at point \(A\), i.e., no movement overall.
This is equivalent to staying at point \(A\), i.e., no movement overall.

Definition Negative Vector
The negative vector of \(\vec{u}\) is the vector with the same direction, the same length, but the opposite sense (orientation). It is denoted by \(-\vec{u}\).
Definition Algebraic Negative Vector
$$-\begin{pmatrix}x\\
y\end{pmatrix}=\begin{pmatrix}-x\\
-y \\
\end{pmatrix}$$
Proposition Negative of \(\Vect{AB}\)
The vector \(\Vect{BA}\) (from \(B\) to \(A\)) is the negative of the vector \(\Vect{AB}\) (from \(A\) to \(B\)):$$\Vect{BA} = -\Vect{AB}$$
To subtract one vector from another, we simply add its negative (opposite).
Definition Subtraction of Vectors
The subtraction of vectors \(\Vect{u} - \Vect{v}\) is defined as adding the negative of the second vector:$$\Vect{u}-\Vect{v} = \Vect{u} + (-\Vect{v})$$
Example
Calculate \(\Vect{AB}-\Vect{CB}\).
$$\begin{aligned}\Vect{AB}-\Vect{CB} &= \Vect{AB} + (-\Vect{CB})\\
&= \Vect{AB} + \Vect{BC}\\
&= \Vect{AC}\end{aligned}$$
Definition Algebraic Vector Subtraction
$$\begin{pmatrix}x\\
y\end{pmatrix}-\begin{pmatrix}x'\\
y'\end{pmatrix}=\begin{pmatrix}x-x'\\
y-y' \\
\end{pmatrix}$$
Scalar Multiplication
Let \(\Vect{v} = \begin{pmatrix} 2\\1\end{pmatrix}\). The notation \(2\Vect{v}\) means \(\Vect{v}+\Vect{v}\). Find the coordinates of the vectors:
- \(\textcolor{olive}{2} \Vect{v}\)
- \(\textcolor{olive}{3} \Vect{v}\)
- \(\vdots\)
- \(\textcolor{olive}{k} \Vect{v}\)
- \(\begin{aligned}[t] \textcolor{olive}{2} \Vect{v} &= \Vect{v} + \Vect{v} \\ &= \begin{pmatrix} 2 \\ 1 \end{pmatrix} + \begin{pmatrix} 2 \\ 1 \end{pmatrix} \\ &= \begin{pmatrix} \textcolor{olive}{2} \times 2 \\ \textcolor{olive}{2} \times 1 \end{pmatrix} \\ &= \begin{pmatrix} 4 \\ 2 \end{pmatrix} \end{aligned}\)
- \(\begin{aligned}[t] \textcolor{olive}{3} \Vect{v} &= \Vect{v} + \Vect{v} + \Vect{v} \\ &= \begin{pmatrix} 2 \\ 1 \end{pmatrix} + \begin{pmatrix} 2 \\ 1 \end{pmatrix} + \begin{pmatrix} 2 \\ 1 \end{pmatrix} \\ &= \begin{pmatrix} \textcolor{olive}{3} \times 2 \\ \textcolor{olive}{3} \times 1 \end{pmatrix} \\ &= \begin{pmatrix} 6 \\ 3 \end{pmatrix} \end{aligned}\)
- \(\vdots\)
- \(\begin{aligned}[t] \textcolor{olive}{k} \Vect{v} &= \Vect{v} + \Vect{v} + \dots + \Vect{v} \quad \text{(\)k\( times)} \\ &= \begin{pmatrix} 2 \\ 1 \end{pmatrix} + \begin{pmatrix} 2 \\ 1 \end{pmatrix} + \dots + \begin{pmatrix} 2 \\ 1 \end{pmatrix} \\ &= \begin{pmatrix} \textcolor{olive}{k} \times 2 \\ \textcolor{olive}{k} \times 1 \end{pmatrix} \end{aligned}\)
Definition Scalar Multiplication
Let \(k\) be a real number. The product \(k\Vect{v}\) is defined by:$$k\begin{pmatrix}x\\
y\end{pmatrix}=\begin{pmatrix}kx\\
ky\end{pmatrix}$$
Remark
- \(2\Vect{v}\) has the same direction and sense as \(\Vect{v}\), and is twice as long.
- \(-2\Vect{v}\) has the same direction but the opposite sense, and is twice as long as \(\Vect{v}\).
- If \(0 < k < 1\), the vector \(k\Vect{v}\) has the same direction and sense as \(\Vect{v}\), but is shorter.
- \(0\Vect{v} = \Vect{0}\), the null vector.
Magnitude of a Vector
By the theorem of Pythagoras,
Proposition Magnitude of a Vector
If \(\Vect{v}=\begin{pmatrix}x\\y\end{pmatrix}\), the magnitude or length of \(\Vect{v}\) is $$\|\Vect{v}\|=\sqrt{x^2+y^2}$$ 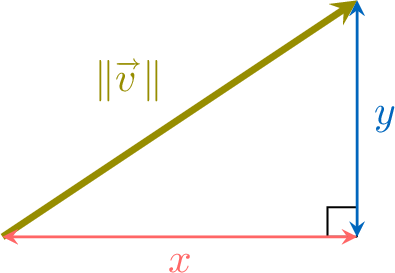

Example
Calculate the length of \(\Vect{v}=\begin{pmatrix}4\\3\\\end{pmatrix}\)
$$\begin{aligned}[t]\|\Vect{v}\| & =\sqrt{4^3+3^2}\\
& =\sqrt{16+9}\\
& =\sqrt{25}\\
&=5 \text{ units}\\
\end{aligned}$$
Proposition Distance between Two Points
The distance between points \(A(x_A, y_A)\) and \(B(x_B, y_B)\) in the plane is the magnitude of the vector \(\Vect{AB}\):$$AB = \|\Vect{AB}\| = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2}$$
Example
Calculate the distance between the points \(A(1,\ 2)\) and \(B(5,\ 5)\).
$$\begin{aligned}[t]AB &= \|\Vect{AB}\|\\
&= \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2} \\
&= \sqrt{(5 - 1)^2 + (5 - 2)^2} \\
&= \sqrt{4^2 + 3^2} \\
&= \sqrt{16 + 9} \\
&= \sqrt{25} \\
&= 5\ \text{units}\end{aligned}$$
Colinearity
Definition Colinear Vectors
Two vectors \(\Vect{u}\) and \(\Vect{v}\) are said to be colinear if there exists a real number \(k\) such that:$$\Vect{u} = k \Vect{v}$$
Remarks
- The components of two colinear vectors are proportional.
- The zero vector \(\Vect{0}\) is colinear with every vector \(\Vect{u}\), since \(\Vect{0} = 0 \cdot \Vect{u}\).
Proposition Colinearity and Geometry
- Two lines \(\Line{AB}\) and \(\Line{CD}\) are parallel if and only if the vectors \(\Vect{AB}\) and \(\Vect{CD}\) are colinear.
- Three points \(A\), \(B\), and \(C\) are collinear (lie on the same straight line) if and only if the vectors \(\Vect{AB}\) and \(\Vect{AC}\) are colinear.
Definition Determinant of Two Vectors
Let \(\Vect{u} = \begin{pmatrix} x \\ y \end{pmatrix}\) and \(\Vect{v} = \begin{pmatrix} x' \\ y' \end{pmatrix}\) be two vectors in the plane. The determinant of \(\Vect{u}\) and \(\Vect{v}\), denoted \(\det(\Vect{u},\,\Vect{v})\), is defined as:$$\det(\Vect{u},\,\Vect{v}) =\begin{vmatrix}x & x' \\
y & y'\end{vmatrix}= x \cdot y' - y \cdot x'$$
Proposition Colinearity and Determinant
Two vectors \(\Vect{u}\) and \(\Vect{v}\) are colinear if and only if$$\det(\Vect{u},\,\Vect{v}) = 0$$
Example
Let \(A(1,\ 2)\), \(B(5,\ 4)\), \(C(-1,\ -1)\), and \(D(5,\ 2)\).
Are the lines \(\Line{AB}\) and \(\Line{CD}\) parallel?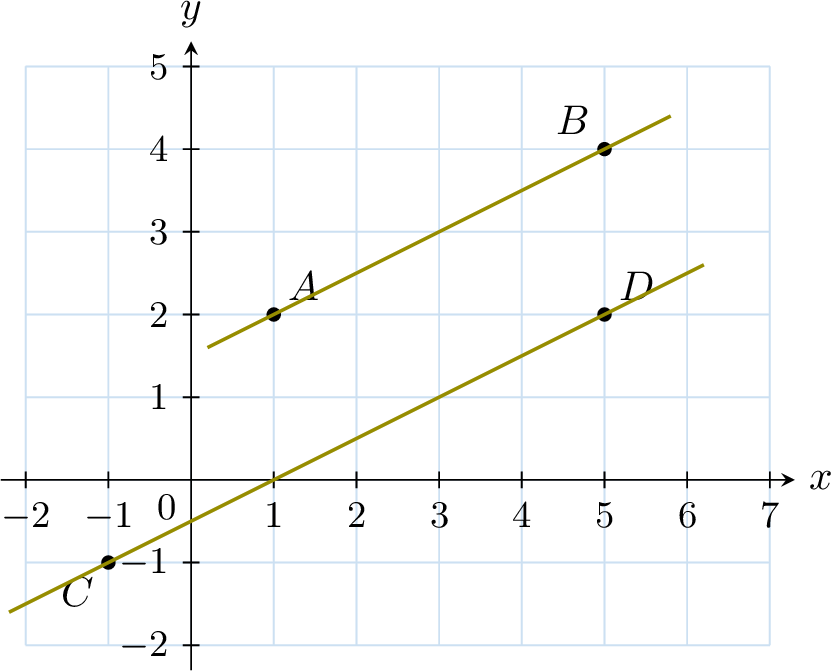
Are the lines \(\Line{AB}\) and \(\Line{CD}\) parallel?
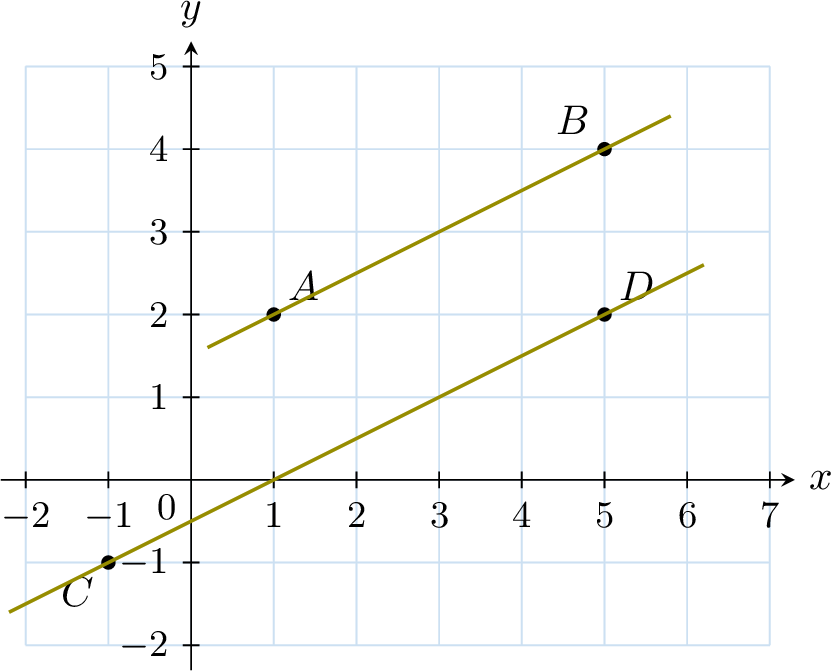
First, compute the vectors:$$\Vect{AB} = \begin{pmatrix}5-1 \\
4-2\end{pmatrix} = \begin{pmatrix}4 \\
2\end{pmatrix}, \quad\Vect{CD} = \begin{pmatrix}5-(-1) \\
2-(-1)\end{pmatrix} = \begin{pmatrix}6 \\
3\end{pmatrix}$$Calculate the determinant:$$\det(\Vect{AB},\,\Vect{CD}) =\begin{vmatrix}4 & 6 \\
2 & 3\end{vmatrix}= 4\times 3 - 6\times 2 = 12 - 12 = 0$$So the determinant is zero. Let's double-check the proportionality:$$\frac{6}{4} = 1.5, \quad \frac{3}{2} = 1.5$$Thus, \(\Vect{CD} = 1.5 \Vect{AB}\), so the vectors are colinear, and the lines are parallel.
Conclusion
In this chapter, we have explored vectors as fundamental tools for describing movement and position in the plane, both geometrically and algebraically. Their strength lies in connecting algebraic operations with geometric intuition, enabling us to model and solve a wide variety of problems in mathematics and science.Vectors are not only essential in geometry but also play a key role in the modern world. In artificial intelligence and data science, for instance, almost all information—images, texts, and even relationships—are encoded as vectors. The landmark paper Attention is All You Need (Vaswani et al., 2017) underlines this fact: modern AI systems, such as OpenAI’s ChatGPT or Grok, manipulate vast arrays of vectors to learn patterns and make predictions. As the authors write:"An attention function can be described as mapping a query and a set of key-value pairs to an output, where the query, keys, values, and output are all vectors." Understanding vectors, therefore, not only builds your geometric and algebraic fluency but also connects you to the mathematical foundations of today's digital and AI-driven world.