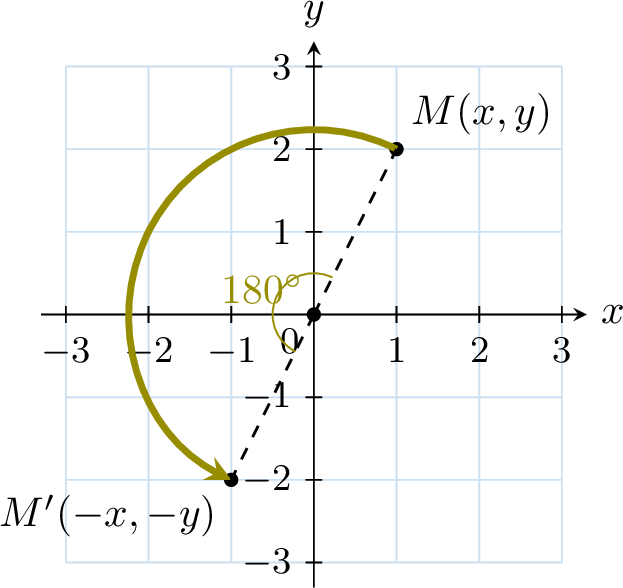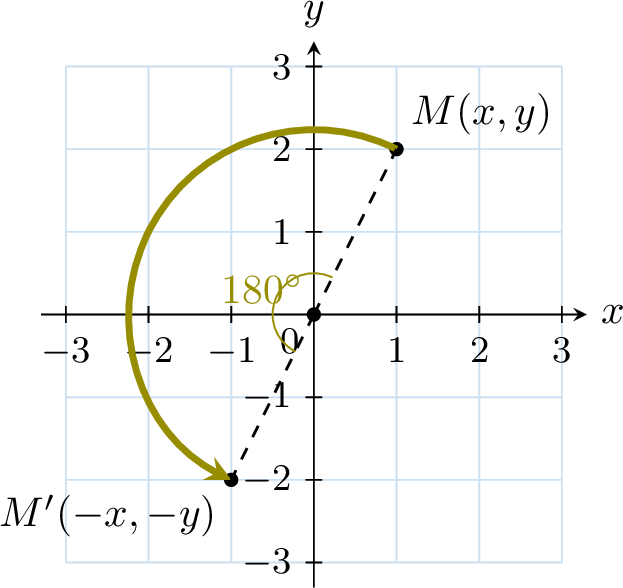Transformations
Types of Transformations
Transformations are ways to move, flip, or turn a shape.
Definition Object and Image
When a transformation is applied to a shape, the input shape is called the object. The output shape after the transformation is called the image.
Definition Types of Transformations
There are several types of transformations, including:
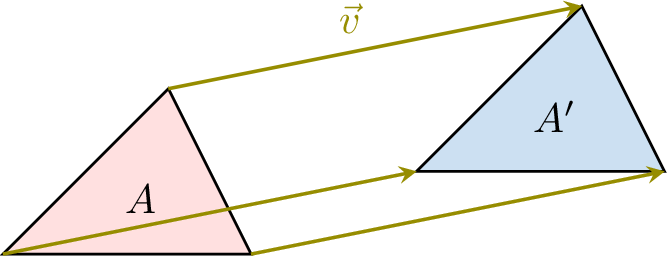
- Translation: Slides the shape to a new position without changing its shape, size, or the direction it faces.
- Reflection: Flips the shape over a line (like a mirror), creating a mirror image.
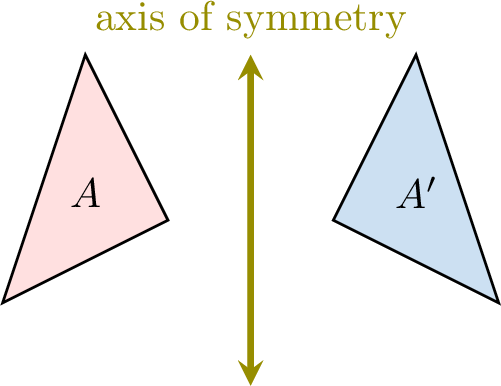
- Rotation: Turns the shape around a point by a certain angle.
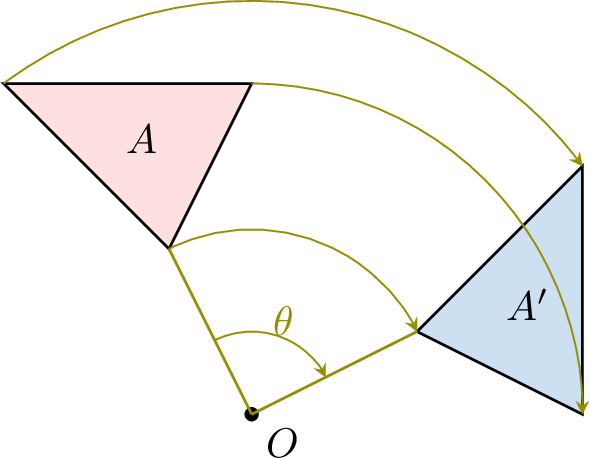
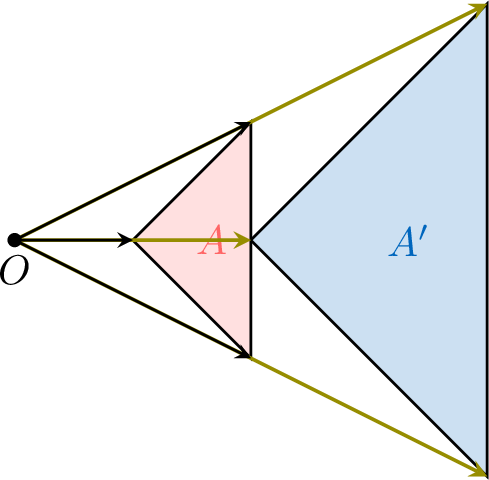
- Homothety: Enlarges or reduces the shape by a scale factor from a center point, keeping the shape similar.
Translation
A translation moves a figure from one place to another. Every point on the figure moves the same distance in the same direction.
Definition Translation
A translation by the vector \(\Vect{v}\) maps a point \(M\) to its image \(M'\) such that \(\Vect{MM'} = \Vect{v}\).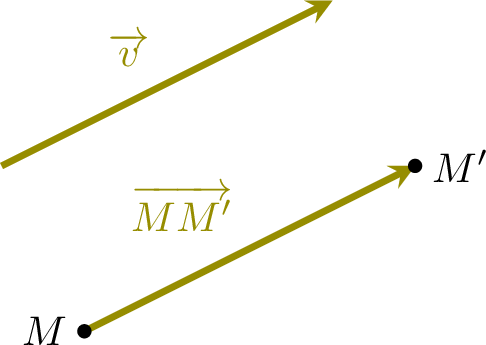

Proposition Coordinates of the Image Point
In a coordinate system, if the point \(M\) has coordinates \((x, y)\) and the translation vector is \(\Vect{v} = \begin{pmatrix} a \\ b \end{pmatrix}\), then the image point \(M'\) has coordinates \((x + a, y + b)\). 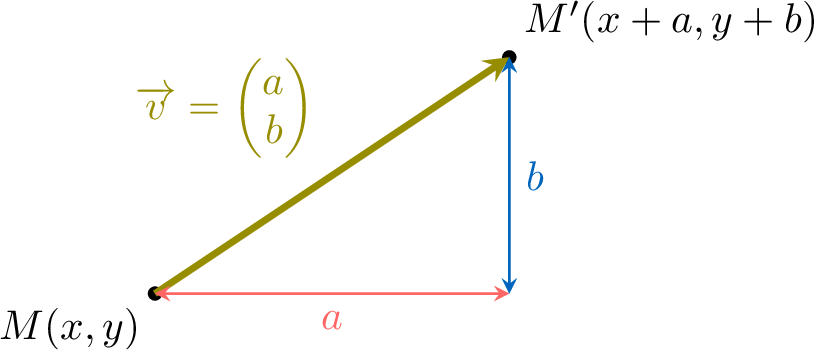

Let \(M'\) be the image point with coordinates \((x', y')\).$$\begin{aligned}\Vect{MM'} &= \Vect{v}\\
\begin{pmatrix} x'-x \\
y'-y \end{pmatrix} &= \begin{pmatrix} a \\
b \end{pmatrix}\\
x'-x =a \text{ and }& y'-y= b\\
x' =x+a \text{ and }& y'= y+b\\
\end{aligned}$$
Homothety
Definition Homothety
A homothety with center \(A\) and scale factor \(\textcolor{olive}{k}\) maps a point \(M\) to the point \(M'\) such that \(M'\) is obtained by translating the point \(A\) by the vector \(\textcolor{olive}{k}\overrightarrow{AM}\).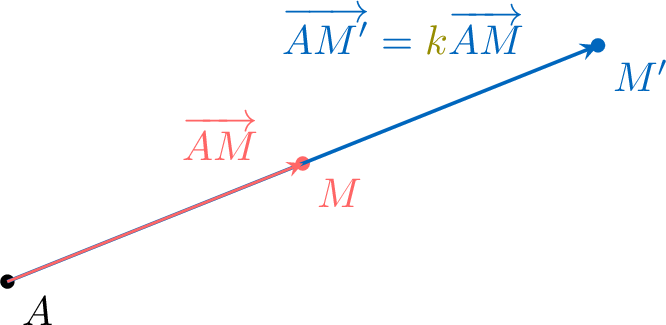
\(\dfrac{\textcolor{colorprop}{AM'}}{\textcolor{colordef}{AM}}=|\textcolor{olive}{k}|\)
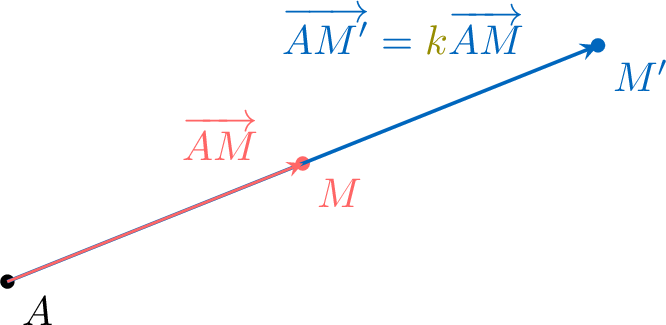
\(\dfrac{\textcolor{colorprop}{AM'}}{\textcolor{colordef}{AM}}=|\textcolor{olive}{k}|\)
Proposition Coordinates of the Image Point
In a coordinate system, if the center \(A\) has coordinates \((a, b)\), the point \(M\) has coordinates \((x, y)\), and the scale factor is \(\textcolor{olive}{k}\), then the image point \(M'\) has coordinates \((a + \textcolor{olive}{k}(x - a),\ b + \textcolor{olive}{k}(y - b))\).
Let \(M'\) be the image point with coordinates \((x', y')\).$$\begin{aligned}\Vect{AM'} &= k \Vect{AM}\\
\begin{pmatrix} x'-a \\
y'-b \end{pmatrix} &= k \begin{pmatrix} x-a \\
y-b \end{pmatrix}\\
x'-a =k(x-a) \text{ and }& y'-b= k(y-b)\\
x' =a+k(x-a) \text{ and }& y'= b+k(y-b)\\
\end{aligned}$$
Specific Reflections
Proposition Reflection over the \(x\)-axis
The image of the point \(M(x, y)\) under the reflection over the \(x\)-axis is \(M'(x, -y)\).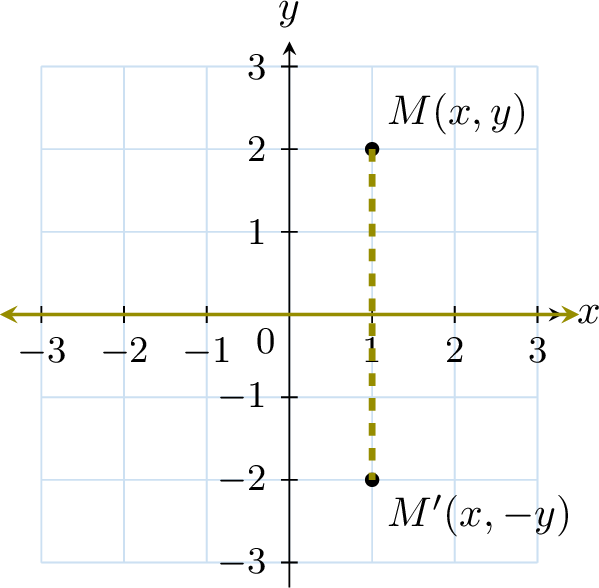
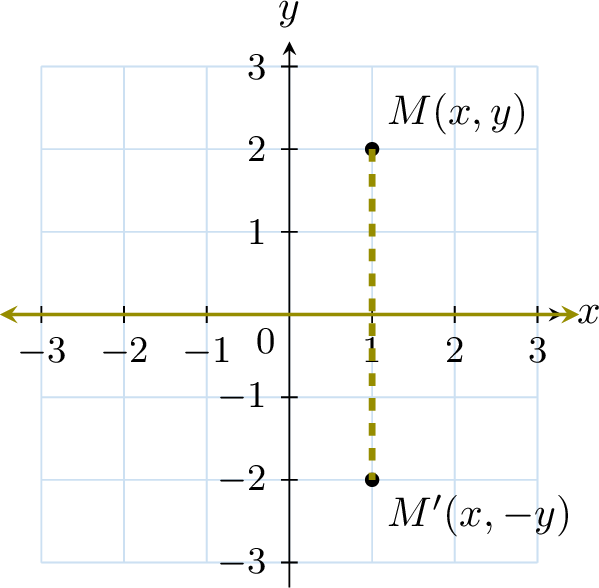
Proposition Reflection over the \(y\)-axis
The image of the point \(M(x, y)\) under the reflection over the \(y\)-axis is \(M'(-x, y)\).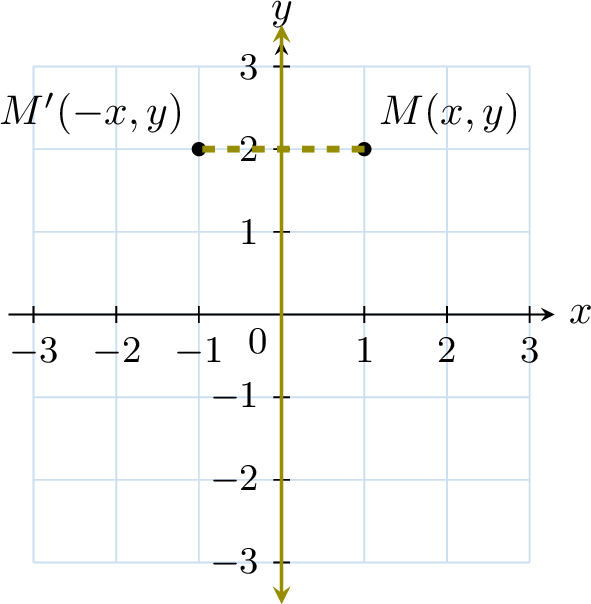
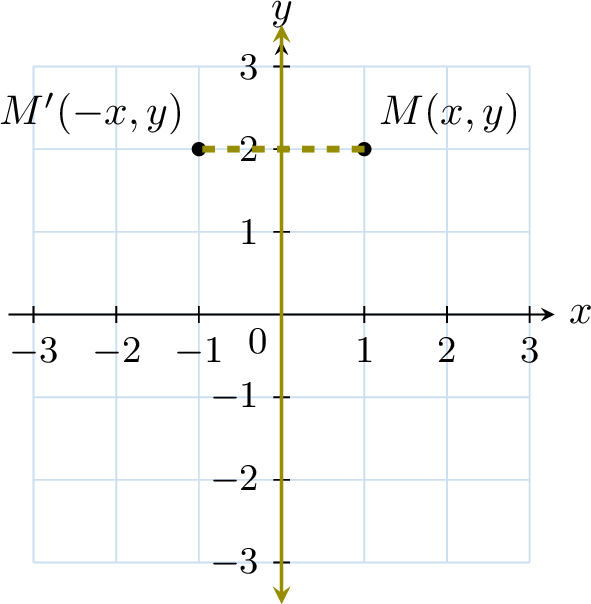
Proposition Reflection over the line \(y\equal x\)
The image of the point \(M(x, y)\) under the reflection \(M_{y=x}\) over the line \(y=x\) is \(M'(y, x)\).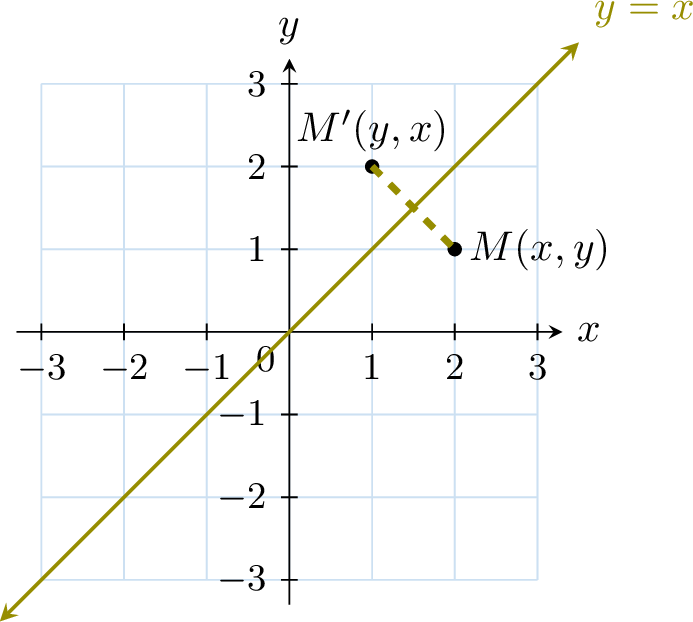
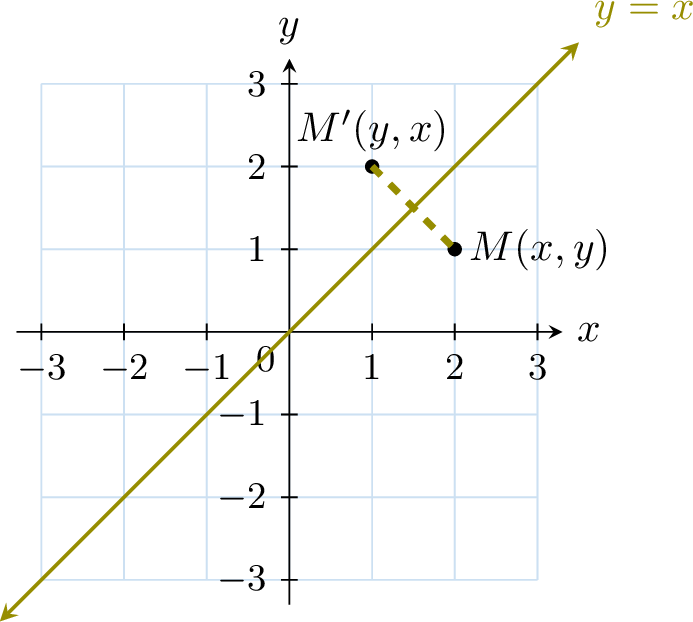
Specific Rotations
Proposition Rotation of 90°
The image of the point \(M(x, y)\) under the rotation of 90° (counterclockwise) around the origin is \(M'(-y, x)\).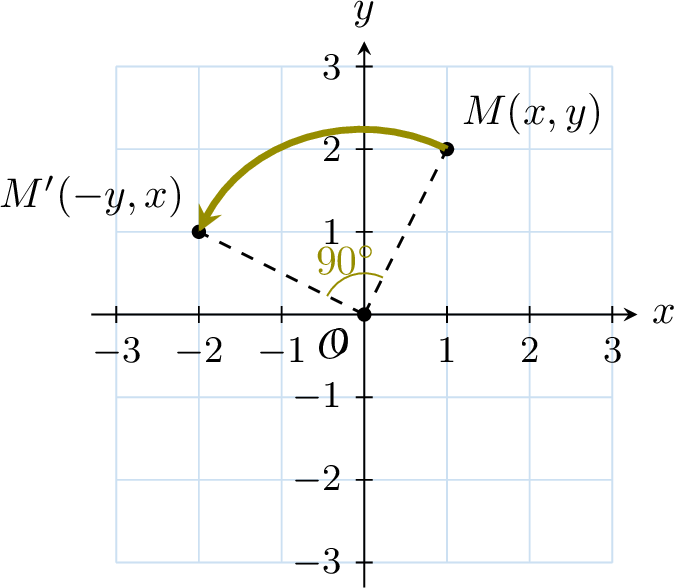
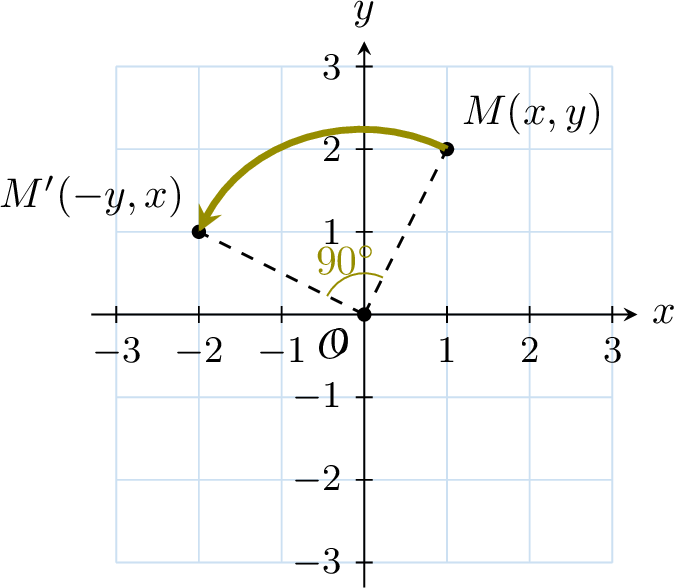
Proposition Rotation of -90°
The image of the point \(M(x, y)\) under the rotation of -90° (clockwise) around the origin is \(M'(y, -x)\).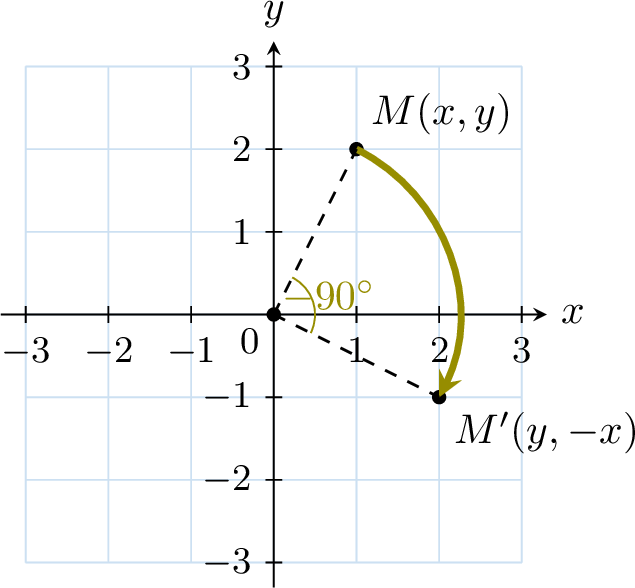
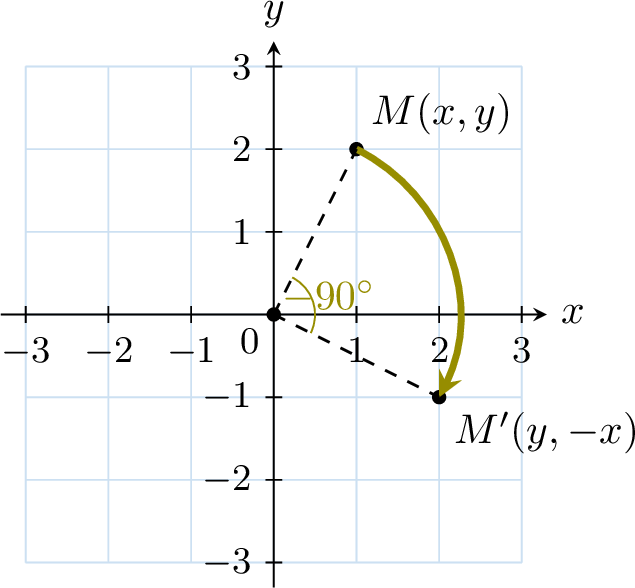
Proposition Rotation of 180°
The image of the point \(M(x, y)\) under the rotation of 180° around the origin is \(M'(-x, -y)\).