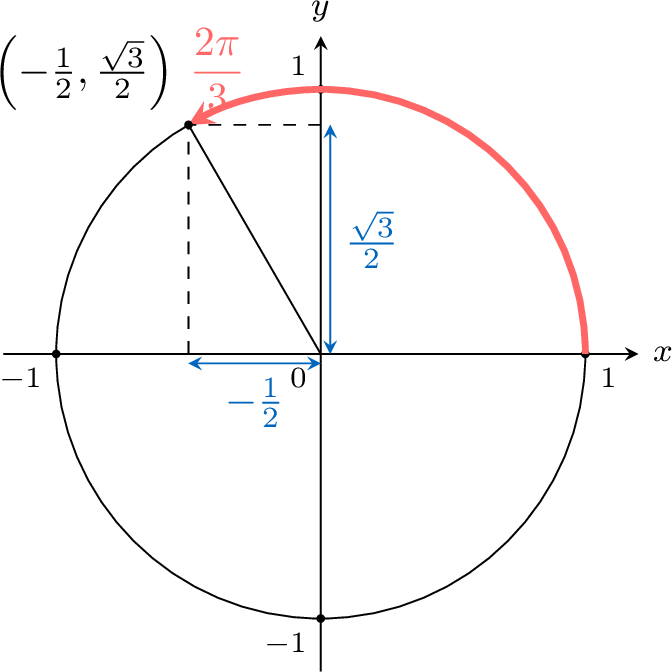
Trigonometry
- The measure of an angle is the fraction of a complete turn. We have seen previously that a full revolution makes an angle of \(360^\circ\).
- An angle can be equal to the length of the arc formed by an angle with the circle of radius 1.
Radian Measure
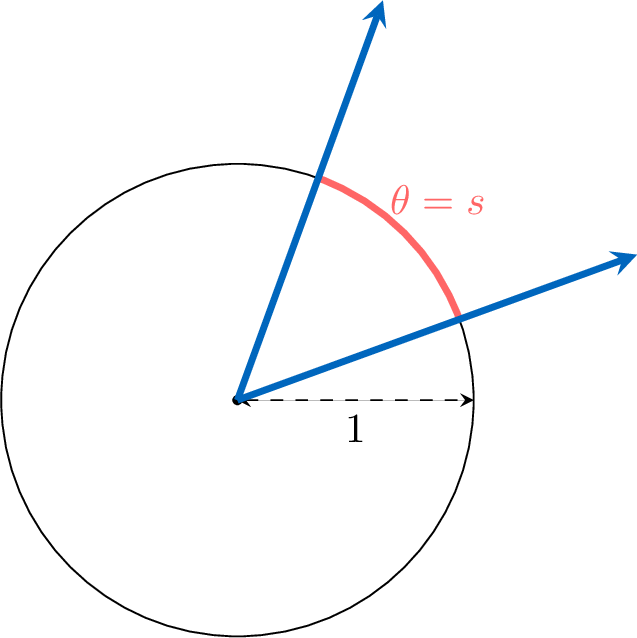
Definition Radian Measure
The radian measure, \(\theta\), of an angle is defined as the length of the arc subtended between the two rays of the angle on a circle of radius 1.

The radian unit is often omitted with 1 rad = 1.
Proposition Angle of Complete Turn
The radian measure of the revolution angle is \(2 \pi\).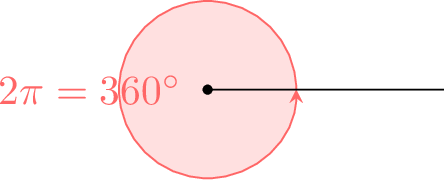

The circumference of the unit circle is \(2 \pi\).
By definition, the revolution angle is equal to the arc length, which is \(2\pi\).
By definition, the revolution angle is equal to the arc length, which is \(2\pi\).
Example
Find the angle of the straight angle 
The straight angle is half the revolution angle. So the angle is \(\frac{2 \pi}{2}=\pi\). 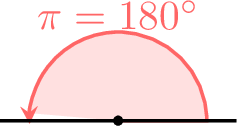
Proposition Proportionality of Radians and Degrees
Radians and degrees are in proportion.
Method Converting Between Degrees and Radians
- To convert from degrees to radians, multiply degrees by \(\frac{\pi}{180}\)
- To convert from radians to degrees, multiply radians by \(\frac{180}{\pi}\)
Example
Convert \(60^{\circ}\) to radians.
\(\begin{aligned}[t]60^{\circ}&=60^{\circ} \times \frac{\pi}{180^{\circ}}\\&=\frac{\pi}{3}\end{aligned}\)
Definition Positive and Negative Angles
- A positive angle measure represents a counterclockwise rotation.
- A negative angle measure represents a clockwise rotation.
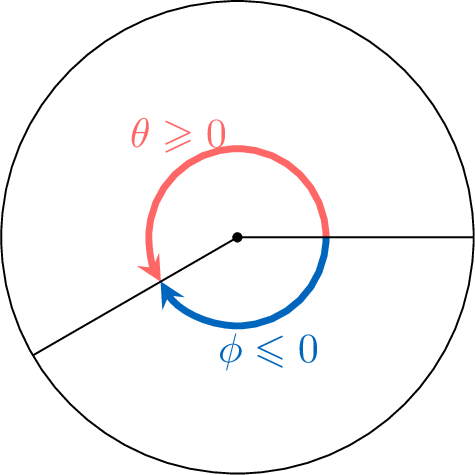
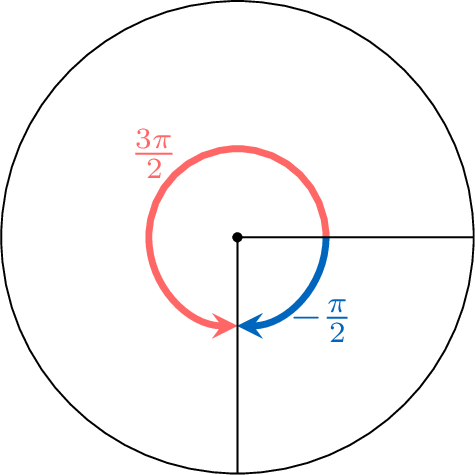
Example
Draw the angle \(\frac{3\pi}{2}\) and \(-\frac{\pi}{2}\)
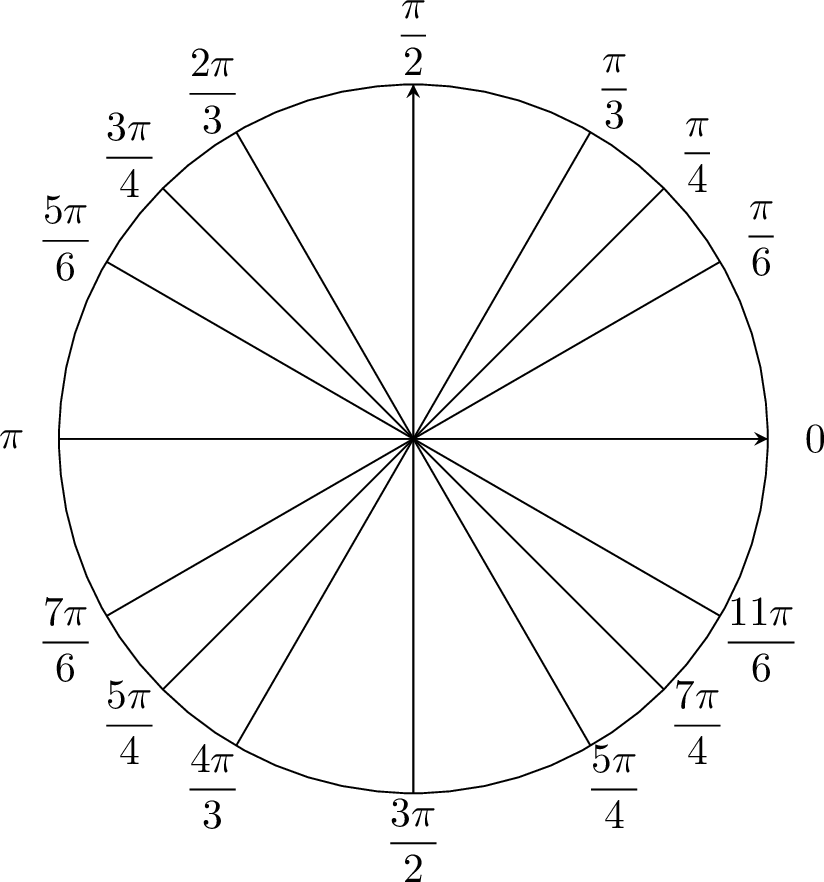
Proposition Reference Angles on the Unit Circle
Trigonometric Ratios and Unit Circle
Definition Unit circle
The unit circle is a circle with a radius of 1 centered at the origin.

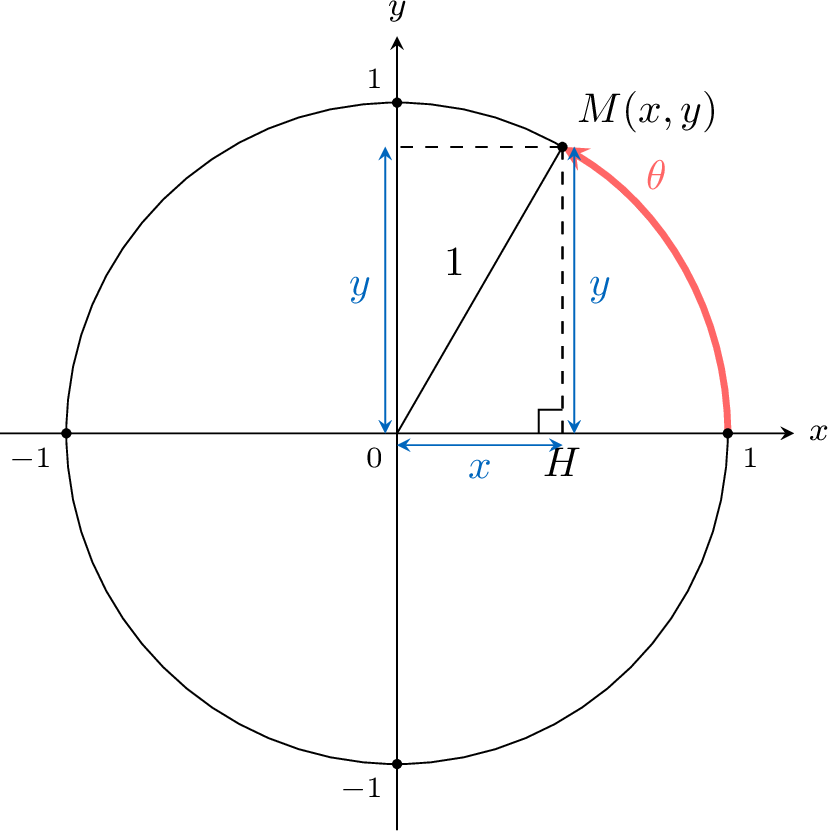
Proposition Relation between Angle and Coordinates
For \(M(x,y)\) the point on the unit circle at the angle \(\theta\), then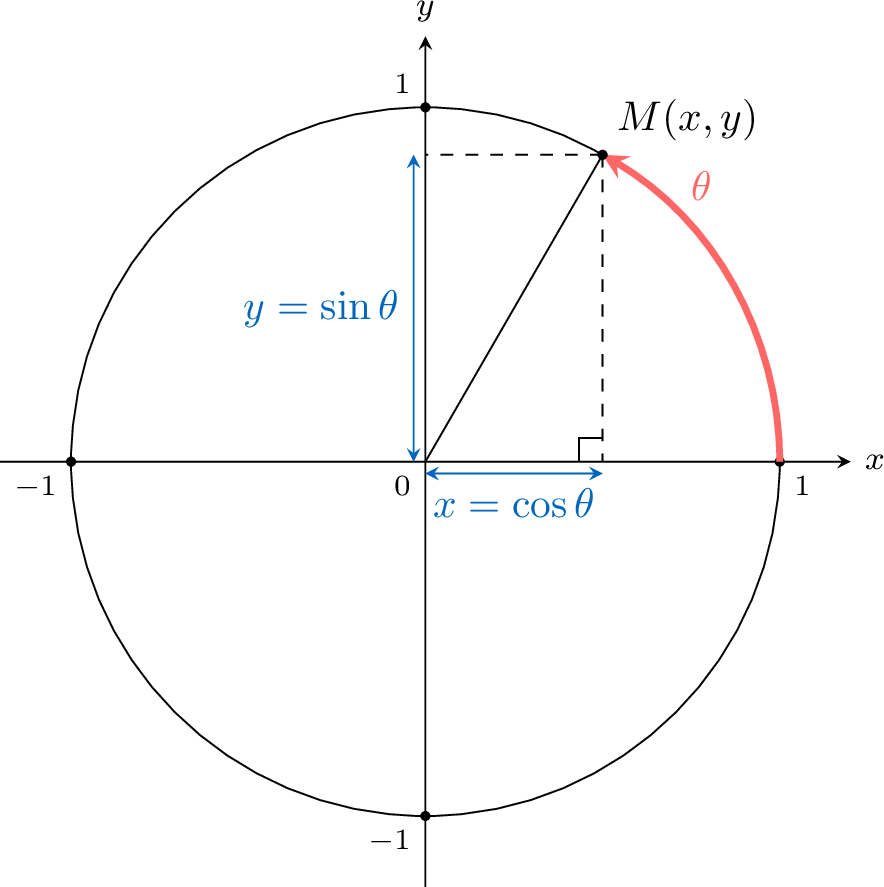
- \(\cos \theta\) is the \(x\)-coordinate of \(M\): \(\cos \theta =x\)
- \(\sin \theta\) is the \(y\)-coordinate of \(M\): \(\sin \theta =y\)

Example
Find the values \(\cos \left(\frac{\pi}{2}\right)\) and \(\sin \left(\frac{\pi}{2}\right)\).
On the unit circle, the point corresponding to the angle \(\frac{\pi}{2}\) has coordinates (0,1):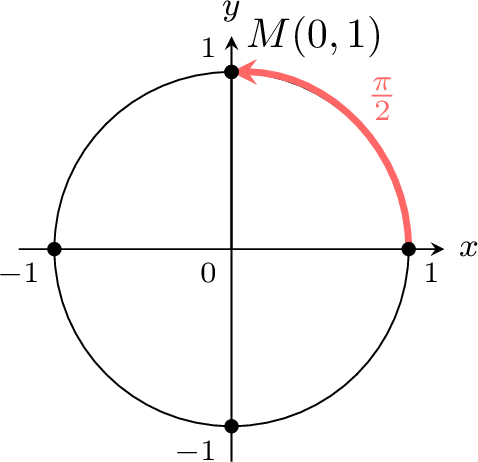
\(\sin \left(\frac{\pi}{2}\right)=1 \quad\) \(y\)-coordinate

\(\sin \left(\frac{\pi}{2}\right)=1 \quad\) \(y\)-coordinate
Proposition Sign of of Sine and Cosine
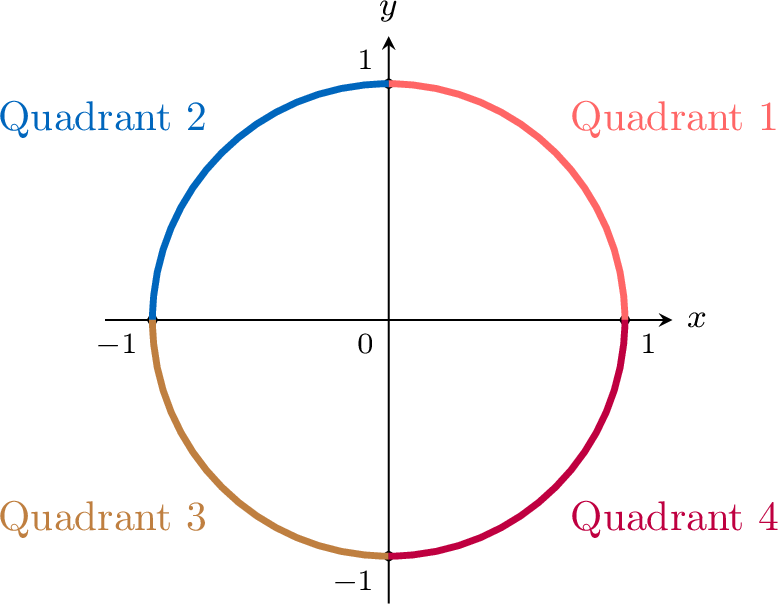
| Quadrant | \(\cos \theta\) | \(\sin \theta\) |
| 1 | \(+\) | \(+\) |
| 2 | \(-\) | \(+\) |
| 3 | \(-\) | \(-\) |
| 4 | \(+\) | \(-\) |
Trigonometric Properties
Proposition Pythagorean Relation
$$\cos ^2 \theta+\sin ^2 \theta=1$$
Let \(M(\cos \theta,\sin\theta)\) the point on the unit circle at the angle \(\theta\).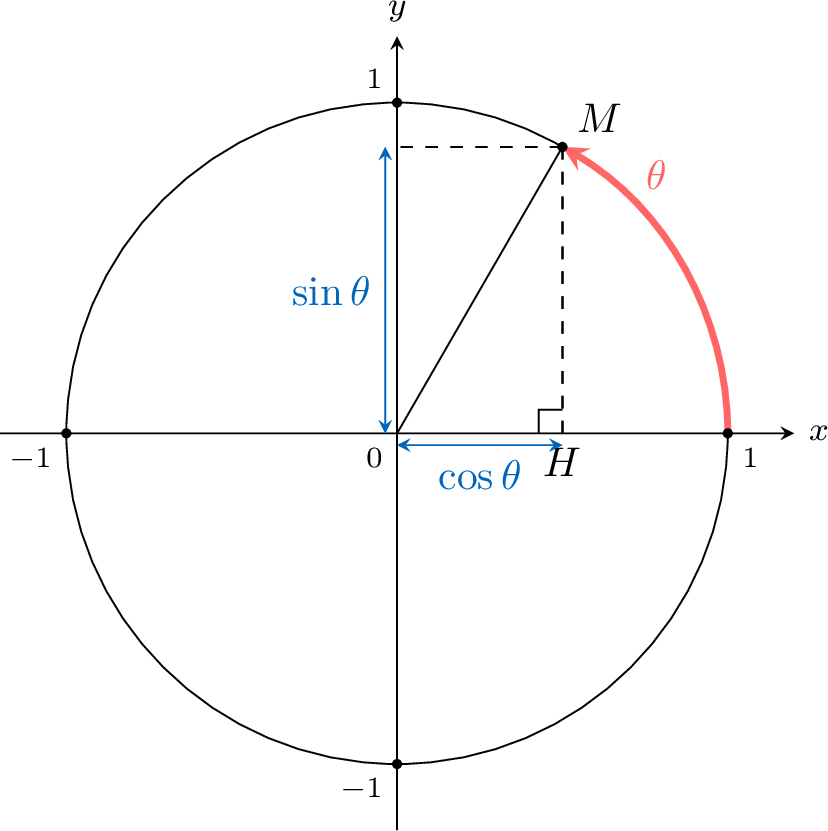

Proposition Maximum and Minimum of Trigonometric Ratios
$$-1 \leqslant \cos \theta \leqslant 1\quad\text{ and }\quad-1 \leqslant \sin \theta \leqslant 1$$
- Geometric proof:

The length \(OH\) lies in \([-1,1]\). As \(OH=\cos \theta\), \(-1 \leqslant \cos \theta \leqslant 1\). - Analytical proof:$$\begin{aligned}0 &\leqslant \sin ^2 \theta&&\text{(square number is positive)} \\ \cos ^2 \theta &\leqslant \cos ^2 \theta +\sin ^2 \theta &&\text{(adding } \cos ^2 \theta\text{ to both sides)} \\ \cos ^2 \theta &\leqslant 1 &&(\cos ^2 \theta+\sin ^2 \theta=1) \\ -1 &\leqslant \cos \theta \leqslant 1 &&\text{(taking square roots, as } \sqrt{\cos^2 \theta} = |\cos \theta| \leqslant 1\text{)} \\ \end{aligned}$$
Proposition Periodicity of Trigonometric Ratios
$$\cos (\theta+2 k \pi)=\cos \theta \quad\text{ and }\quad\sin (\theta+2 k \pi)=\sin \theta $$where \(k\) is any integer.
Let \(M(\cos \theta,\sin\theta)\) the point on the unit circle at the angle \(\theta\).
Let \(M'(\cos(\theta+2\pi),\sin(\theta+2\pi))\) the point on the unit circle at the angle \(\theta+2\pi\).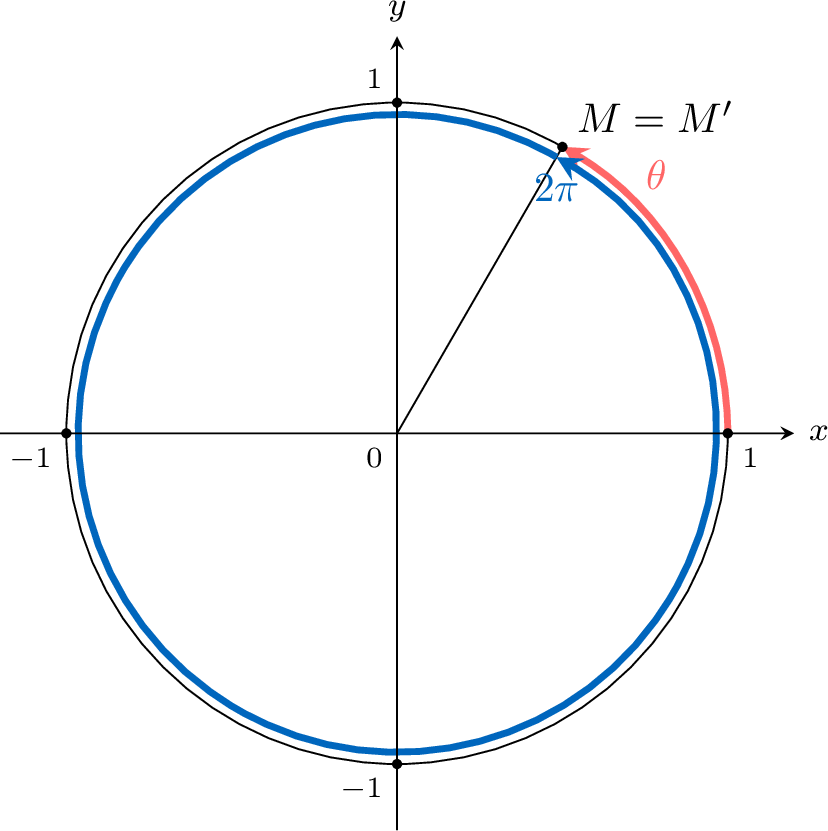
Thus, \(\cos (\theta+2 \pi)=\cos \theta\) and \(\sin (\theta+2 \pi)=\sin \theta\).
The proof extends to any multiple of \(2\pi\), i.e., for integer \(k\).
Let \(M'(\cos(\theta+2\pi),\sin(\theta+2\pi))\) the point on the unit circle at the angle \(\theta+2\pi\).

Thus, \(\cos (\theta+2 \pi)=\cos \theta\) and \(\sin (\theta+2 \pi)=\sin \theta\).
The proof extends to any multiple of \(2\pi\), i.e., for integer \(k\).
Proposition Add \(\pi\) to Trigonometric Ratios
$$\begin{aligned}\sin (\pi+\theta)=-\sin \theta \\
\cos (\pi+\theta)=-\cos \theta\end{aligned}$$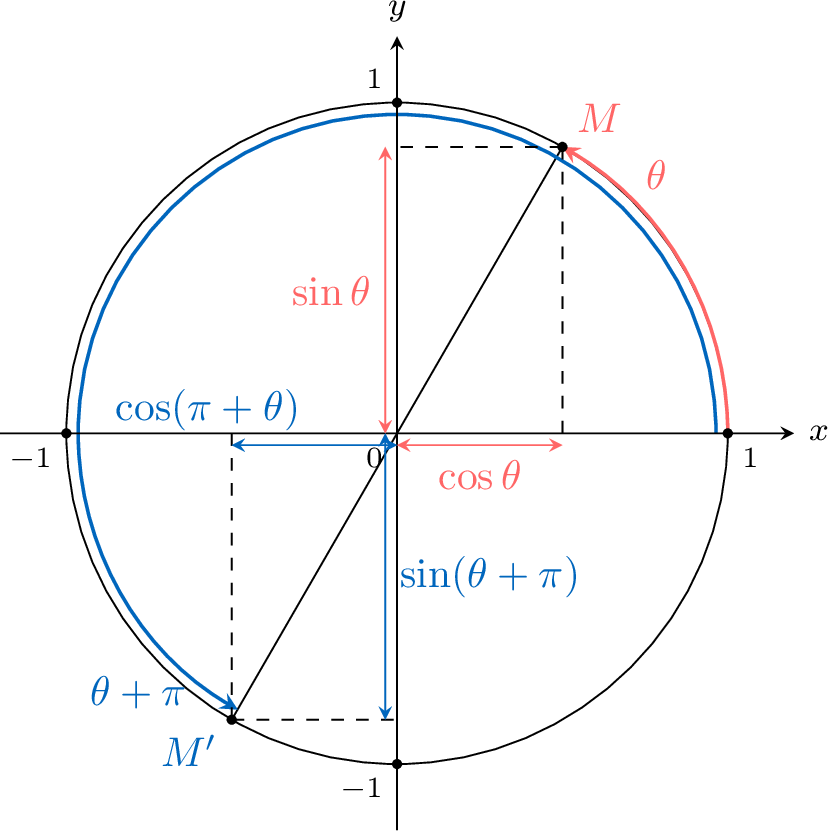
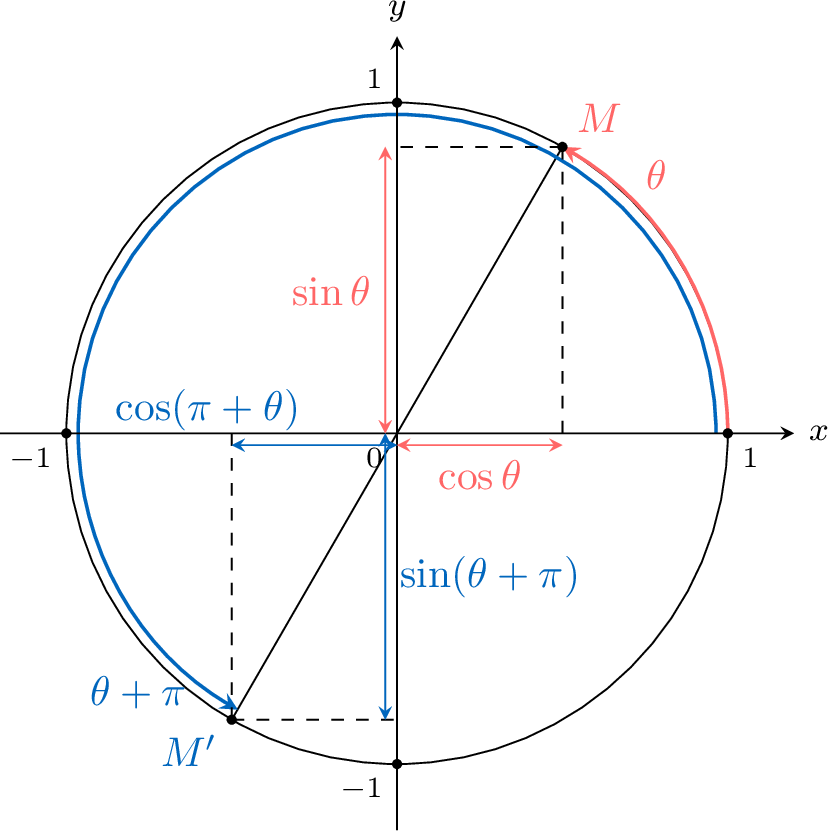
Let \(\theta\) an angle.
Let \(M(\cos \theta,\sin\theta)\) the point on the unit circle at the angle \(\theta\).
Let \(M'(\cos(\pi+\theta),\sin(\pi+\theta))\) the point on the unit circle at the angle \(\pi+\theta\).
As the rotation of angle \(\pi\) is the point reflection through the origin \(O\), the coordinates of \(M'\) are the opposites of the coordinates of \(M\).
So \(\begin{aligned}[t]\sin (\pi+\theta)=-\sin \theta \\\cos (\pi+\theta)=-\cos \theta\end{aligned}\)
Let \(M(\cos \theta,\sin\theta)\) the point on the unit circle at the angle \(\theta\).
Let \(M'(\cos(\pi+\theta),\sin(\pi+\theta))\) the point on the unit circle at the angle \(\pi+\theta\).
As the rotation of angle \(\pi\) is the point reflection through the origin \(O\), the coordinates of \(M'\) are the opposites of the coordinates of \(M\).
So \(\begin{aligned}[t]\sin (\pi+\theta)=-\sin \theta \\\cos (\pi+\theta)=-\cos \theta\end{aligned}\)
Proposition Opposite of Trigonometric Ratios
$$\begin{aligned}\sin (-\theta)=-\sin \theta \\
\cos (-\theta)=\cos \theta\end{aligned}$$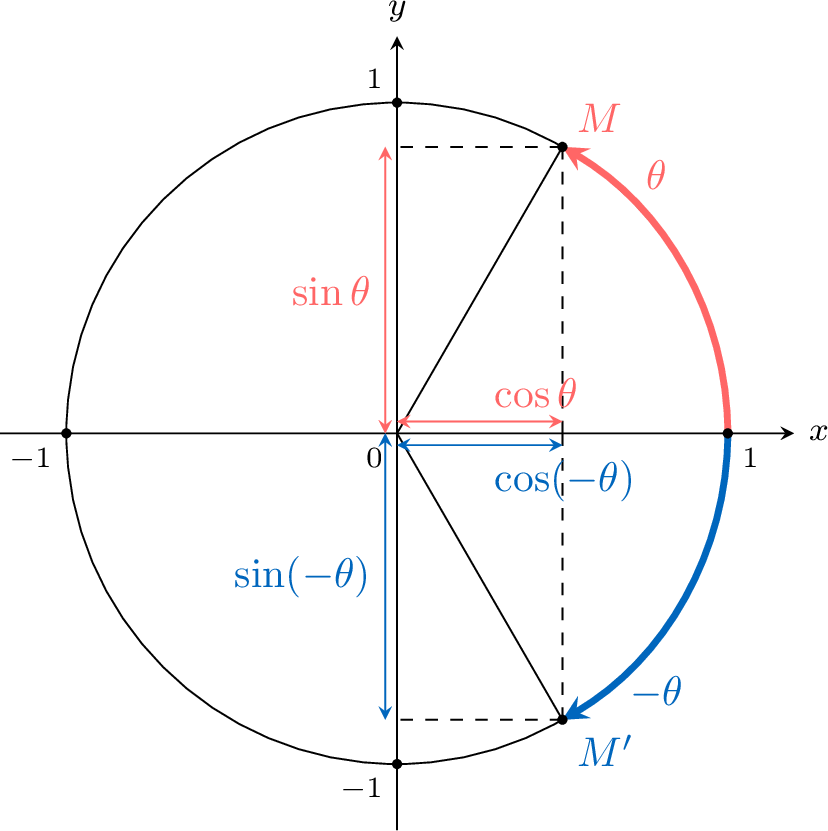

Let \(M(\cos \theta,\sin\theta)\) the point on the unit circle at the angle \(\theta\).
Let \(M'(\cos(-\theta),\sin(-\theta))\) the point on the unit circle at the angle \(-\theta\).
As \(M'\) is the reflection over the x-axis of \(M\), the x-coordinate of \(M'\) is the same as \(M\), and the y-coordinate of \(M'\) is the opposite of \(M\)'s y-coordinate.
So \(\begin{aligned}[t]\sin (-\theta)=-\sin \theta \\\cos (-\theta)=\cos \theta\end{aligned}\)
Let \(M'(\cos(-\theta),\sin(-\theta))\) the point on the unit circle at the angle \(-\theta\).
As \(M'\) is the reflection over the x-axis of \(M\), the x-coordinate of \(M'\) is the same as \(M\), and the y-coordinate of \(M'\) is the opposite of \(M\)'s y-coordinate.
So \(\begin{aligned}[t]\sin (-\theta)=-\sin \theta \\\cos (-\theta)=\cos \theta\end{aligned}\)
Proposition Identities with \(\frac{\pi}{2} - x\)
$$\begin{aligned}\cos\left(\frac \pi 2 -\theta\right) = \sin \theta \\
\sin\left(\frac \pi 2 -\theta\right) = \cos \theta \\
\end{aligned}$$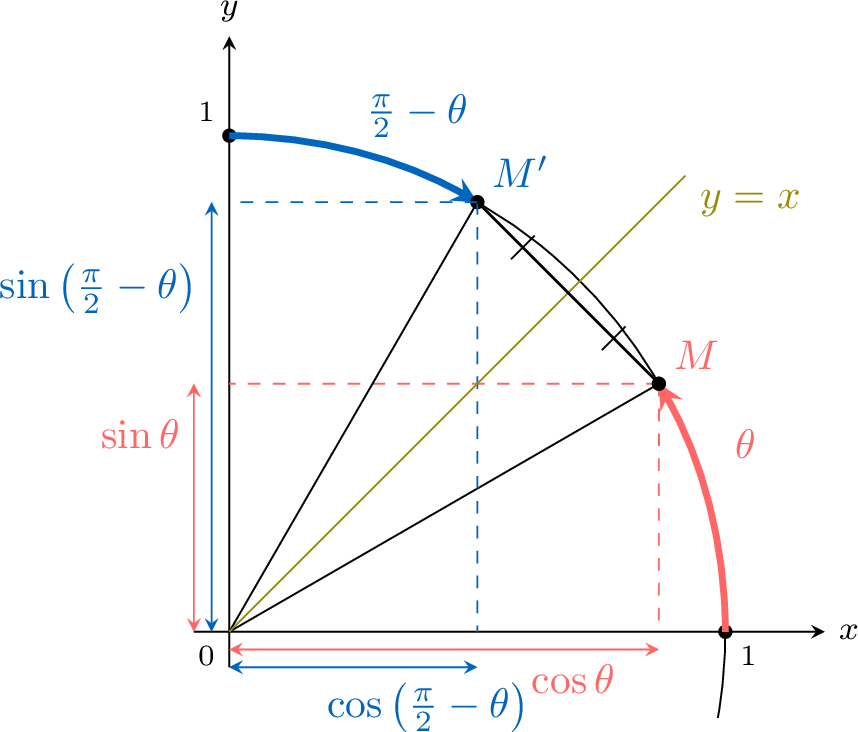

Let \(\theta\) an angle.
Let \(M(\cos \theta,\sin\theta)\) the point on the unit circle at the angle \(\theta\).
Let \(M'(\cos(\frac \pi 2 -\theta),\sin(\frac \pi 2 -\theta))\) the point on the unit circle at the angle \(\frac \pi 2 -\theta\).
As the point \(M\) is the reflection over the line \(y=x\) of \(M'\), the \(x\)-coordinate of \(M\) is the \(y\)-coordinate of \(M'\), and the \(y\)-coordinate of \(M\) is the \(x\)-coordinate of \(M'\).
So \(\begin{aligned}[t]\cos\left(\frac \pi 2 -\theta\right) = \sin \theta \\\sin\left(\frac \pi 2 -\theta\right) = \cos \theta \\\end{aligned}\)
Let \(M(\cos \theta,\sin\theta)\) the point on the unit circle at the angle \(\theta\).
Let \(M'(\cos(\frac \pi 2 -\theta),\sin(\frac \pi 2 -\theta))\) the point on the unit circle at the angle \(\frac \pi 2 -\theta\).
As the point \(M\) is the reflection over the line \(y=x\) of \(M'\), the \(x\)-coordinate of \(M\) is the \(y\)-coordinate of \(M'\), and the \(y\)-coordinate of \(M\) is the \(x\)-coordinate of \(M'\).
So \(\begin{aligned}[t]\cos\left(\frac \pi 2 -\theta\right) = \sin \theta \\\sin\left(\frac \pi 2 -\theta\right) = \cos \theta \\\end{aligned}\)
Multiples of \(\frac{\pi}{4}\)
Proposition Coordinates of Angle \(\frac{\pi}{4}\)
$$\cos \frac{\pi}{4}=\frac{1}{\sqrt{2}} \quad \text { and } \quad \sin \frac{\pi}{4}=\frac{1}{\sqrt{2}}$$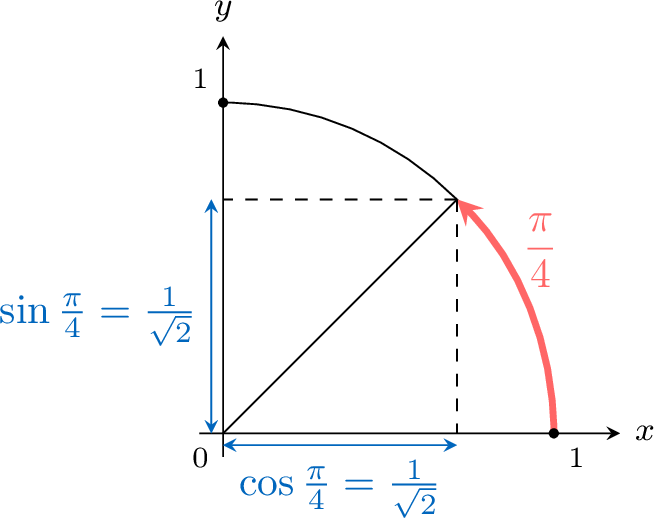
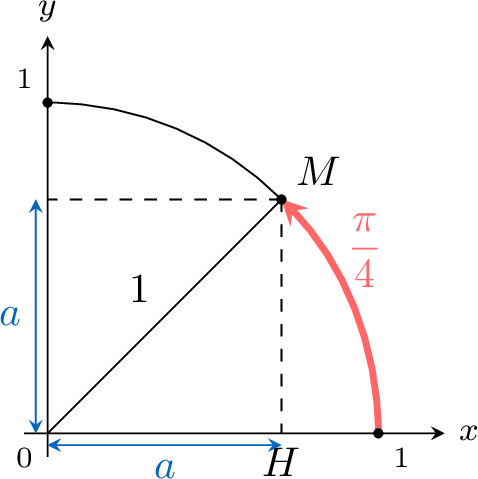
As \(\angle{OMH}=\angle{MOH}\), the triangle \(OHM\) is isosceles.
Let \(a=OH=HM\).$$\begin{aligned} a^2+a^2 &=1^2 \quad \text { Pythagorean theorem for the right triangle } OHM\\ 2 a^2 &=1 \\ a^2 &=\frac{1}{2} \\ a &=\frac{1}{\sqrt{2}} \quad \text { as } a\geqslant 0 \end{aligned}$$So \(M\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)\).
As \(\cos \theta\) is the \(x\)-coordinate of \(M\) and \(\sin \theta\) is the \(y\)-coordinate of \(M\),$$\cos \frac{\pi}{4}=\frac{1}{\sqrt{2}} \quad \text { and } \quad \sin \frac{\pi}{4}=\frac{1}{\sqrt{2}}$$
Proposition Multiples of \(\frac{\pi}{4}\)
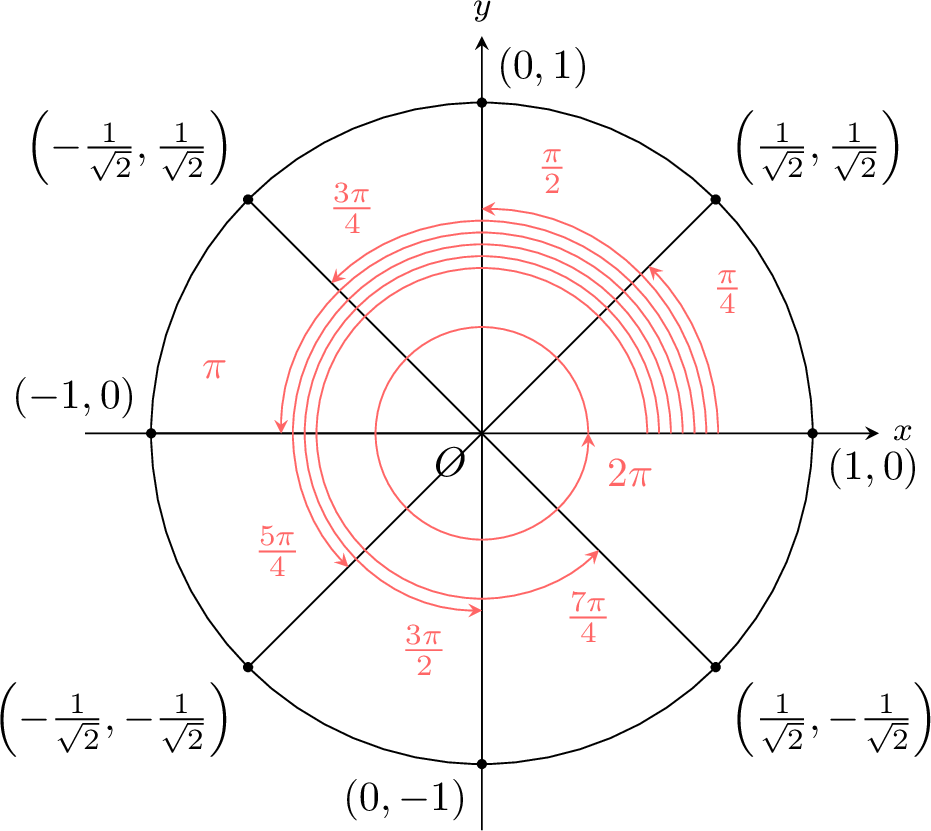
The coordinates of each point are found by reflection symmetries over the axes or the origin.
The signs of the coordinates are determined by the quadrant in which the angle lies.
Example
Find \(\cos \frac{3 \pi}{4}\)
\(\cos \frac{3 \pi}{4} = -\frac{1}{\sqrt{2}}\)
Multiples of \(\frac{\pi}{6}\)
Proposition Coordinates of Angle \(\frac{\pi}{3}\)
$$\cos \frac{\pi}{3}=\frac{1}{2} \quad \text { and } \quad \sin \frac{\pi}{3}=\frac{\sqrt{3}}{2}$$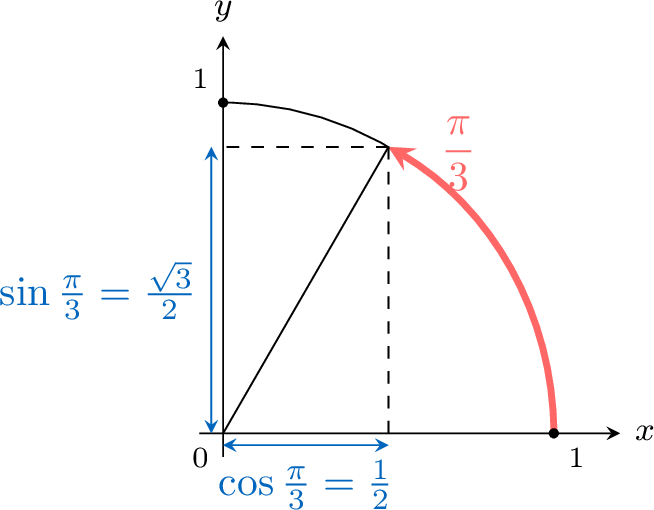

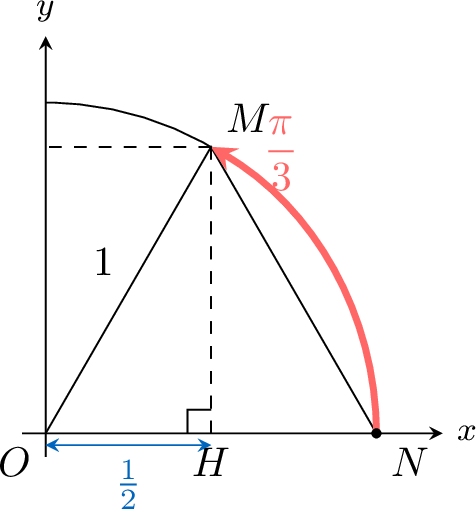
As \(ON=OM=1\), the triangle \(OMN\) is isosceles. So \(\angle{MON}=\angle{MNO}=\frac \pi 3\).
As the sum of angles in a triangle is \(\pi\), \(\angle{OMN}=\frac \pi 3\).
So the triangle \(OMN\) is equilateral.
The altitude \(MH\) bisects the base \(ON\).
So \(OH=\frac{1}{2}\).$$\begin{aligned} OH^2+HM^2 &=OM^2 \quad \text { Pythagorean theorem for the right triangle } OHM\\ \left(\frac{1}{2}\right)^2 + HM^2 &=1 \\ HM^2 &=\frac{3}{4} \\ HM &=\frac{\sqrt{3}}{2} \quad \text { as } HM\geqslant 0 \end{aligned}$$As \(\cos \theta\) is the \(x\)-coordinate of \(M\) and \(\sin \theta\) is the \(y\)-coordinate of \(M\):$$\cos \frac{\pi}{3}=\frac{1}{2} \text { and } \sin \frac{\pi}{3}=\frac{\sqrt{3}}{2}$$
Proposition Multiples of \(\frac{\pi}{6}\)

The coordinates of each point are found by reflection symmetries over the axes or the origin.
Example
Find \(\cos \frac{2 \pi}{3}\) and \(\sin \frac{2 \pi}{3}\)