Inequalities
Inequalities are common in real-world contexts, such as budgeting, temperature ranges, or constraints in optimization problems.
Definition
Definition Inequality
An inequality is a mathematical statement that compares two expressions using symbols such as \(<\), \(>\), \(\leq\), or \(\geq\). Unlike equations, which state equality, inequalities describe a range of possible values that satisfy the relationship.
Example
\(x + 3 < 5\) means that \(x + 3\) is less than 5, and we need to find all values of \(x\) that make this true.
Properties of Inequalities
Proposition Properties of Inequality
Inequalities follow specific rules when performing operations:
- Adding or subtracting the same number from both sides preserves the inequality direction.
- Multiplying or dividing both sides by a positive number preserves the inequality direction.
- Multiplying or dividing both sides by a negative number reverses the inequality direction.
- If \(a < b\) and \(b < c\), then \(a < c\) (transitive property).
Example
- For \(2x < 8\). Dividing both sides by 2 (a positive number) gives \(x < 4\).
- For \(-2x < 8\), dividing by \(-2\) (a negative number) reverses the inequality, giving \(x > -4\).
Method Solving Linear Inequality
To solve a linear inequality, isolate the variable using the properties of inequalities.
Example
Solve \(3x - 5 \leq 10\).
$$\begin{aligned}3x - 5 &\leq 10 \\
3x &\leq 15 && \text{(add 5 to both sides)} \\
x &\leq 5 && \text{(divide by 3)}\end{aligned}$$The solution is \(x \leq 5\), which includes all numbers less than or equal to 5.
Table of Signs
The table of signs is a visual tool used to study the sign (positive, negative, or zero) of a product or quotient of algebraic expressions.
Method Table of Signs for a Product
To construct a table of signs for a product:
- Find the zeros of each factor (solve when each factor equals zero).
- Place these values in order on a number line, dividing it into intervals.
- Determine the sign of each factor in every interval.
- Deduce the sign of the product in each interval using the sign rule (the product is positive if there is an even number of negative factors, negative if there is an odd number).
Example
Study the sign of the expression \((x-2)(x-1)\).
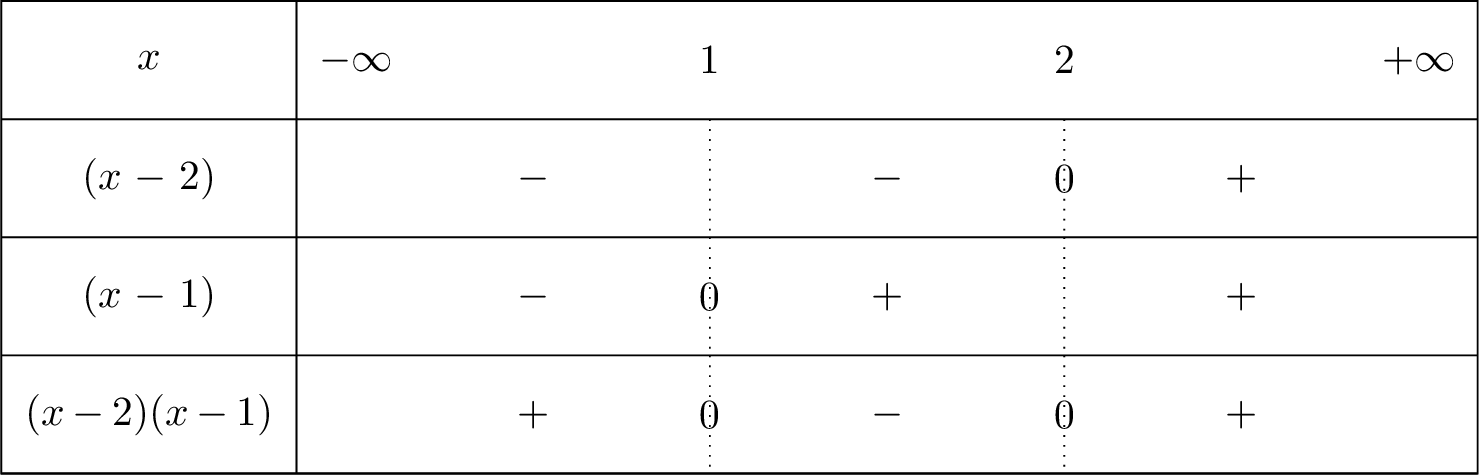
- The sign changes at the zeros: for \((x-2)\) at \(x=2\), for \((x-1)\) at \(x=1\).
- \((x-2)\geqslant 0 \) for \(x\geqslant 2\) and \((x-1)\geqslant 0 \) for \(x\geqslant 1\)
- The sign of the product \((x-2)(x-1)\) is determined by multiplying the signs of the two factors in each interval.