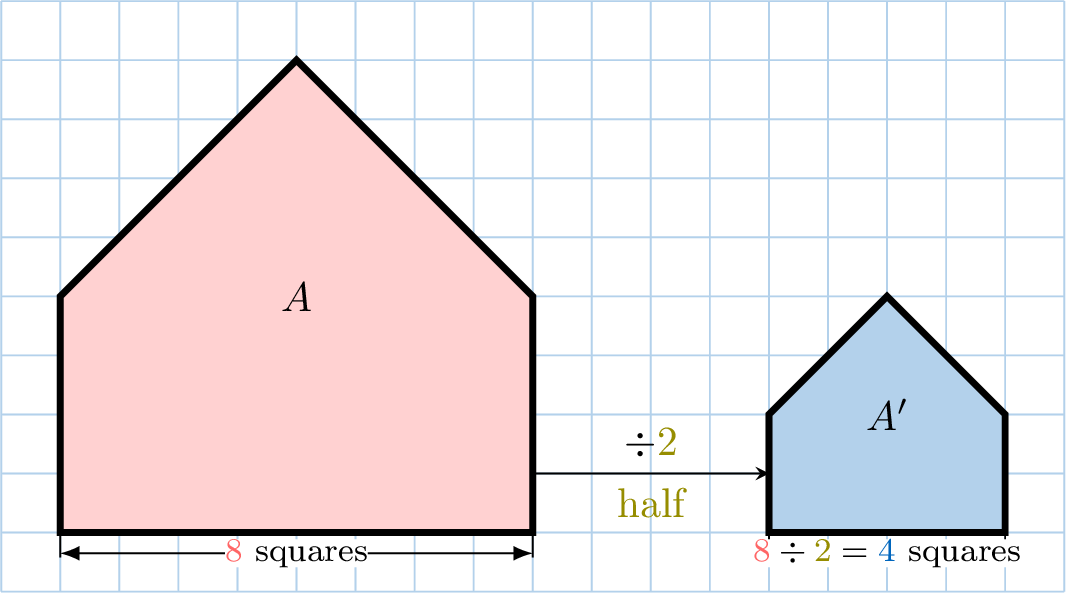
Enlargement and Reduction
Definitions
Look at the rectangles below. They have the same shape but different sizes because their side lengths grow or shrink by the same multiplier.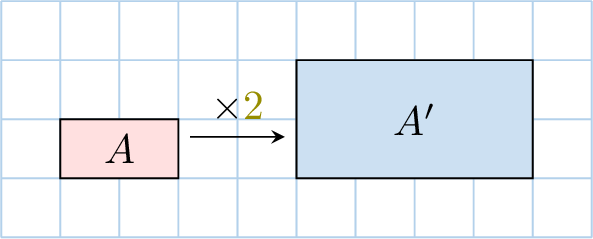

Definition Enlargement and Reduction
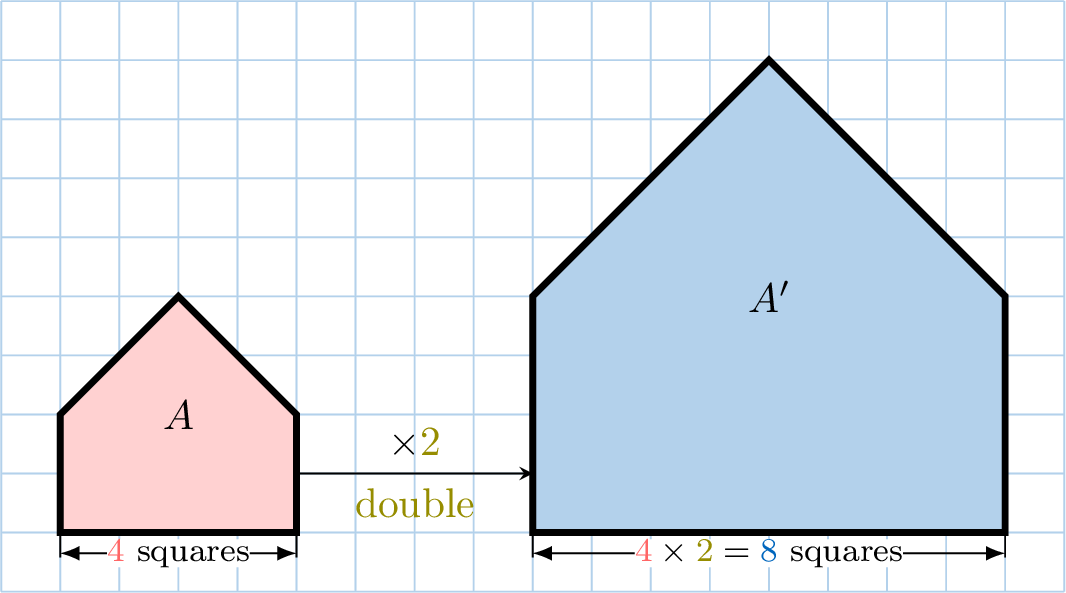
- An enlargement makes a shape larger by multiplying all side lengths by a number called the scale factor.
- A reduction makes a shape smaller by dividing all side lengths by a number called the scale factor.