Properties of Quadrilaterals
Quadrilateral Classification
Definition Quadrilateral
A quadrilateral is a polygon with four sides.

Definition Parallelogram
A parallelogram is a quadrilateral with two pairs of opposite sides parallel.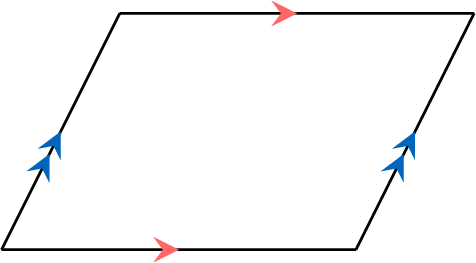

Definition Square
A square is a quadrilateral with four right angles and four equal sides.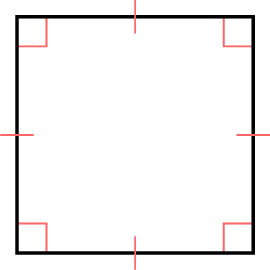

Definition Rectangle
A rectangle is a quadrilateral with four right angles.

Definition Rhombus
A rhombus is a quadrilateral with four equal sides.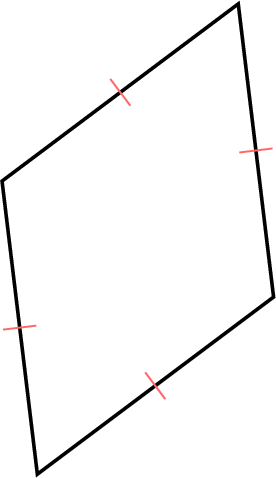

Definition Trapezium
A trapezium is a quadrilateral with one pair of opposite sides parallel.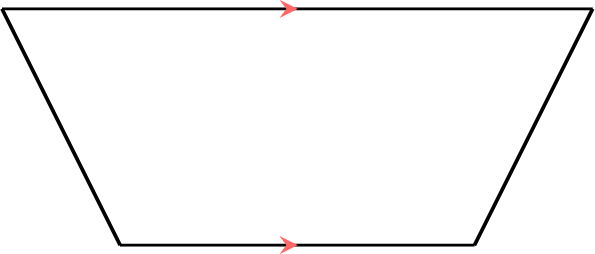

Properties
Proposition Properties of a Parallelogram
- The opposite sides are equal in length.
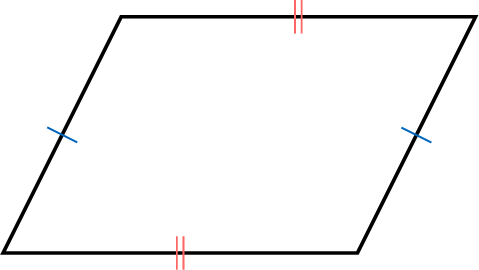
- The opposite angles are equal.

- The adjacent angles are supplementary.

- The diagonals bisect each other.
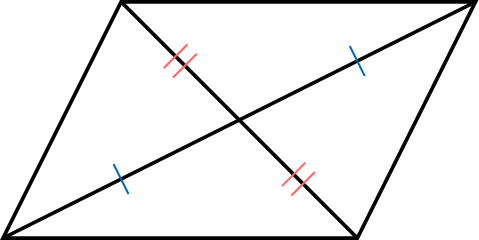
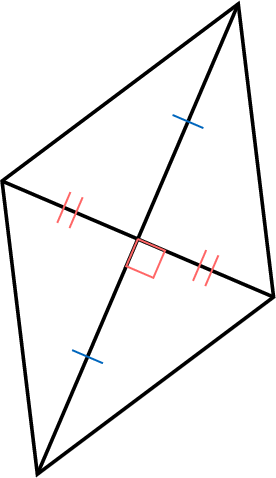
Proposition Properties of a Square
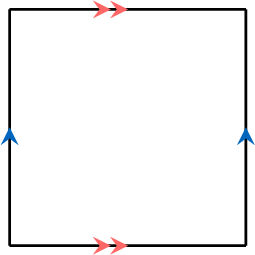
- The opposite sides are parallel.
- The diagonals bisect each other at right angles and are equal in length.
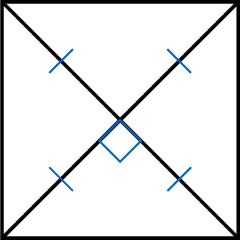
Proposition Properties of a Rectangle
- The opposite sides are equal in length.
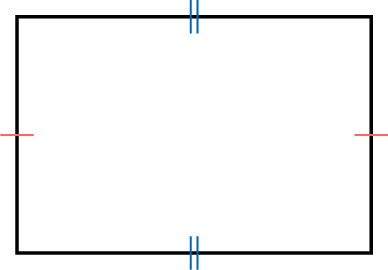
- The opposite sides are parallel.
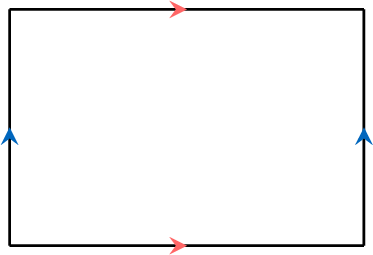
- The diagonals bisect each other and are equal in length.
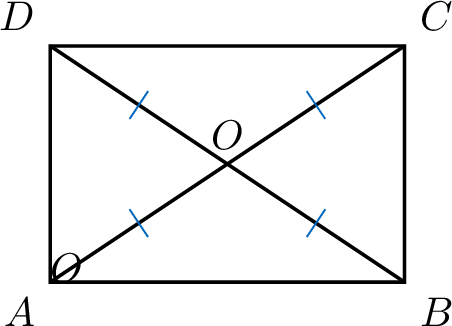
Proposition Properties of a Rhombus
- The opposite sides are parallel.
- The opposite angles are equal.
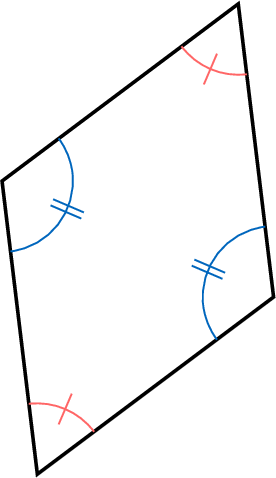
- The adjacent angles are supplementary.

- The diagonals bisect each other at right angles.
Angles
Proposition Sum of the Angles of a Quadrilateral
The sum of the angles of a quadrilateral is \(360^\circ\).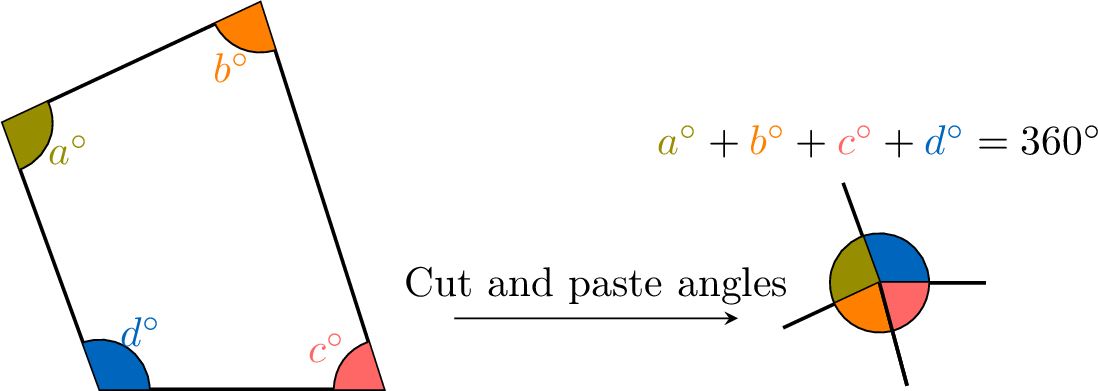

We divide the quadrilateral \(ABCD\) into two triangles, \(ABC\) and \(ACD\), using the diagonal \(AC\).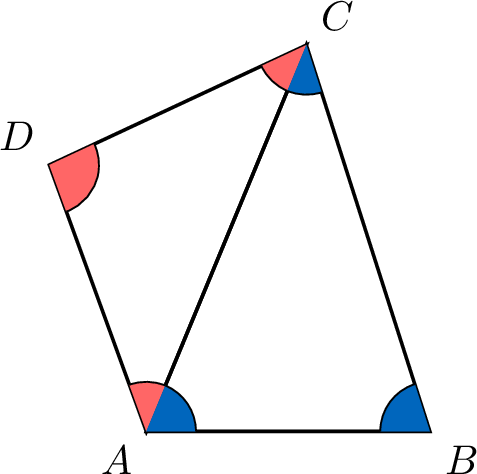

Example
Find the unknown angle \(x^\circ\).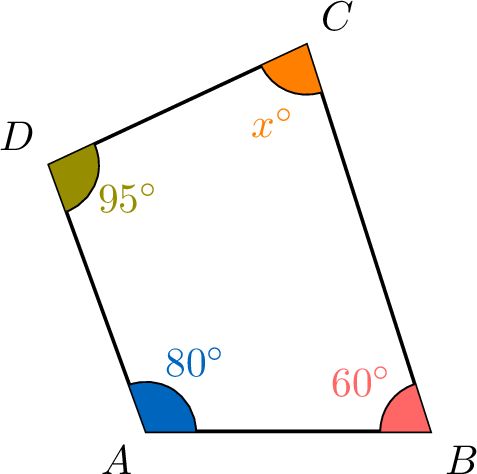

The sum of the angles of a quadrilateral is \(360^\circ\). Given angles \(60^\circ\), \(95^\circ\), and \(80^\circ\):$$\begin{aligned}x^\circ + 95^\circ + 80^\circ + 60^\circ &= 360^\circ \\x^\circ + 235^\circ &= 360^\circ \quad \text{(Adding known angles)} \\x^\circ &= 360^\circ - 235^\circ \quad \text{(Subtracting 235 from both sides)} \\x^\circ &= 125^\circ\end{aligned}$$