Properties of Triangles
Types of Triangles
Definition Triangle
A triangle is a polygon with three sides.

Definition Isosceles triangle
An isosceles triangle is a triangle in which two sides are equal in length. The third side is called the base, and the vertex opposite the base is called the apex.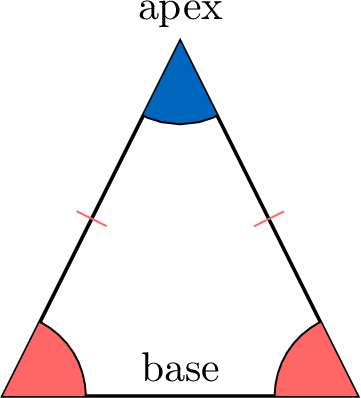

Definition Equilateral triangle
An equilateral triangle is a triangle whose three sides are equal in length. It is a special case of an isosceles triangle.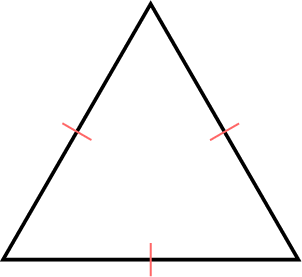

Definition Right-angled triangle
A right-angled triangle is a triangle with one right angle (\(90^\circ\)). The side opposite the right angle is called the hypotenuse.

Definition Scalene triangle
A scalene triangle is a triangle whose three sides have different lengths.

Angles
- Draw any triangle.
- Mark each angle of the triangle with a different color.

- Cut out each angle of the triangle by removing the colored regions around each vertex.
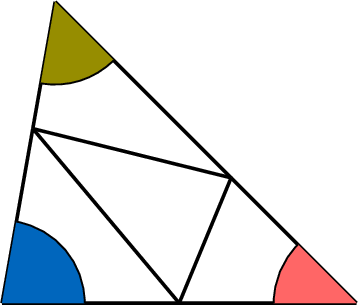
- Arrange the cut-out angles so that they are adjacent, with their vertices meeting at a single point and no overlapping.
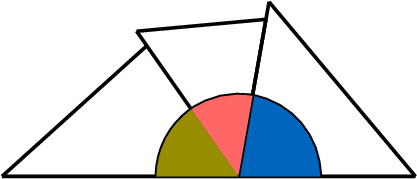
- Observe that the angles form a straight angle (an angle measuring 180°). Since a straight angle measures 180°, the sum of the angles of the triangle is 180°.
Proposition Sum of the angles of a triangle
In any triangle, the sum of the angles is \(180^\circ\).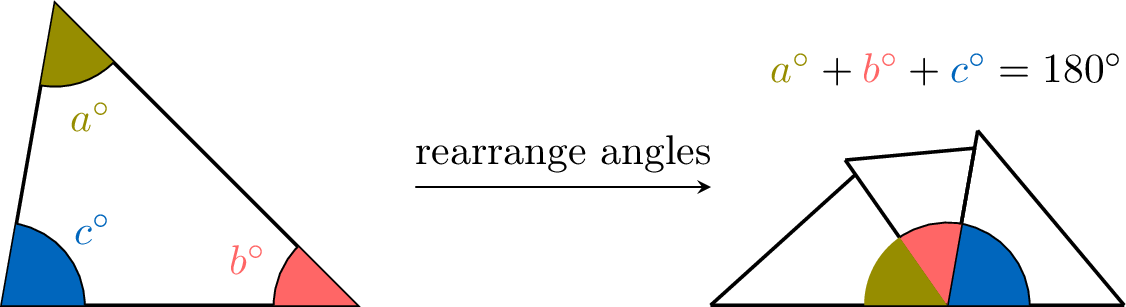

Example
Find the angle \(x^\circ\).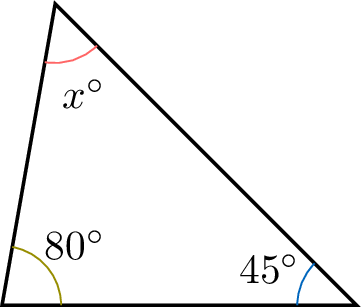

The sum of the angles in a triangle is \(180^\circ\). Therefore:$$\begin{aligned}[t]x^\circ + 45^\circ + 80^\circ &= 180^\circ \\x^\circ + 125^\circ &= 180^\circ \\x^\circ &= 180^\circ - 125^\circ \\x^\circ &= 55^\circ\end{aligned}$$
Proposition Angles for an isosceles triangle
In any isosceles triangle, the angles opposite the equal sides (base angles) are equal.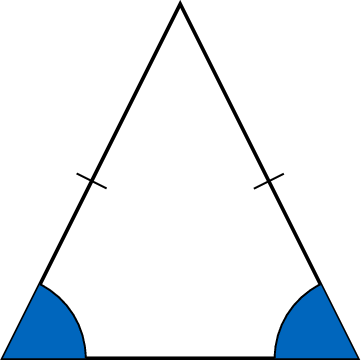

- Draw any isosceles triangle with two equal sides.
- Draw the median from the apex to the midpoint of the base, dividing the triangle into two halves. Shade each half differently.
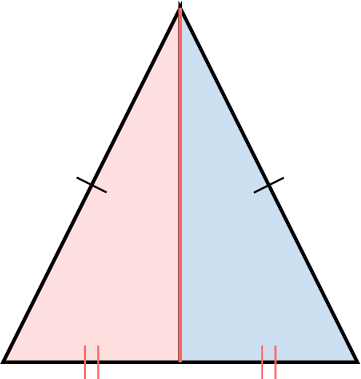
- Cut out the isosceles triangle and fold it along the median. The median is an axis of symmetry because the two equal sides align.
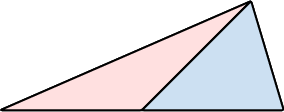
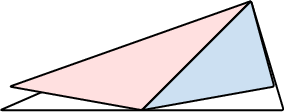
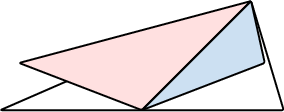

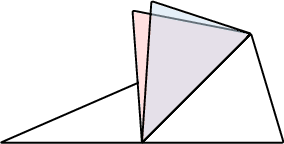

- Observe that the two halves coincide when folded, showing that the base angles are equal due to symmetry.
Proposition Angles for an equilateral triangle
In any equilateral triangle, each angle measures \(60^\circ\).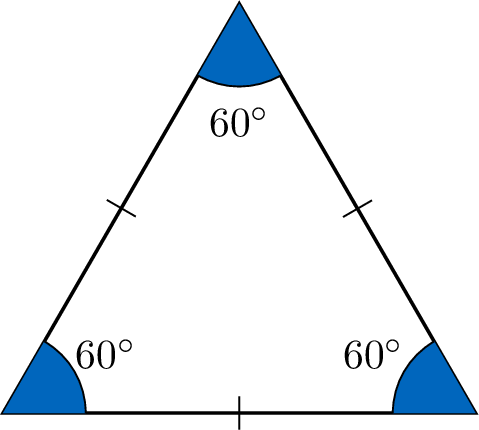

Consider an equilateral triangle with all sides equal. Since the angles opposite equal sides are equal, all three angles are equal, say \(x^\circ\).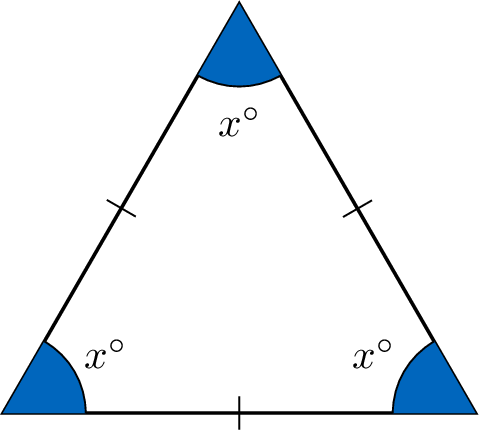

Triangle Inequality Theorem
- Align 4 toothpicks end-to-end to form one side of a triangle.
- Using 9 toothpicks, is it possible to construct a triangle with one side having a length of 5 toothpicks?
-
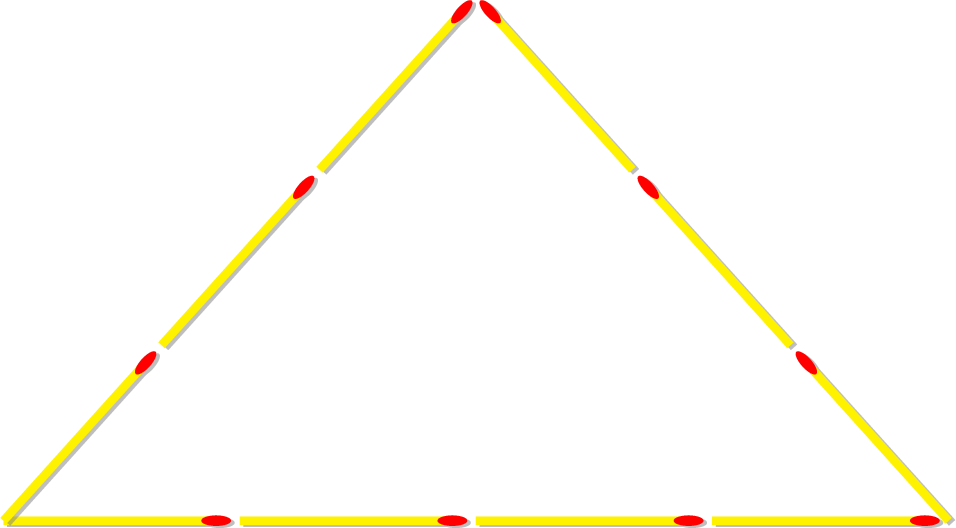
- Place 5 toothpicks end-to-end to form one side of the triangle.
- This leaves 4 toothpicks to form the other two sides.
- Suppose the second side uses 1 toothpick. Then, the third side uses the remaining 3 toothpicks.
- Try to form a triangle with sides of 5, 1, and 3 toothpicks. When you attempt to connect the endpoints of the 5-toothpick side with the 1-toothpick and 3-toothpick sides, the 1-toothpick side is too short to reach the endpoint of the 3-toothpick side, preventing the sides from forming a closed shape.

- Try another combination, such as using 2 toothpicks for each of the other two sides. Again, when you attempt to connect the endpoints of the 5-toothpick side with two 2-toothpick sides, the sides do not meet to form a closed shape because the 5-toothpick side is too long compared to the other two. No combination of the 4 remaining toothpicks (e.g., 1 and 3, or 2 and 2) allows the sides to connect properly, suggesting that the length of one side must relate to the sum of the other two to form a triangle.
Theorem Triangle inequality theorem
In a triangle, the length of each side must be less than the sum of the lengths of the other two sides.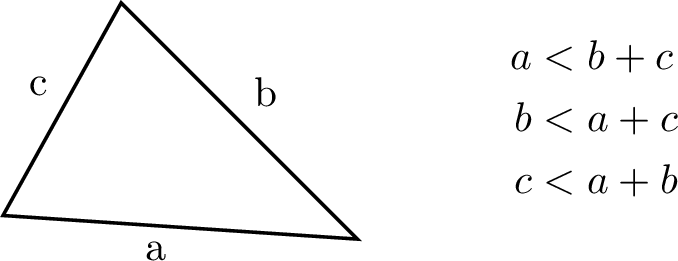
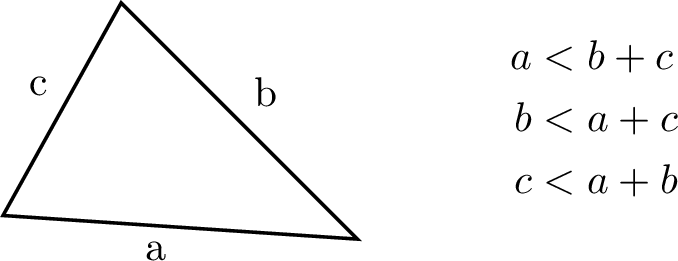
- If one side is longer than the sum of the other two sides, the sides cannot form a triangle because they do not meet to close the shape.

- If one side equals the sum of the other two sides, the result is a degenerate triangle (a straight line), which is not considered a triangle.

Example
Could these be the side lengths of a triangle?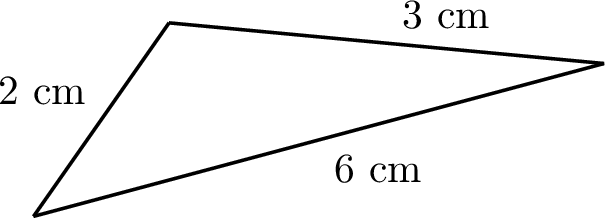

The triangle inequality theorem states that each side must be less than the sum of the other two sides. Check for all three sides:
- \(2 < 6 + 3 = 9\) (holds)
- \(3 < 6 + 2 = 8\) (holds)
- \(6 \not< 3 + 2 = 5\) (does not hold)