Homothety
Definitions
Definition Homothety of a Point
The homothety of point \(M\) with center \(O\) and scale factor \(\textcolor{olive}{k}\) is the point \(M'\) such that \(M'\) is the translation of point \(O\) by the vector \(\textcolor{olive}{k}\overrightarrow{OM}\).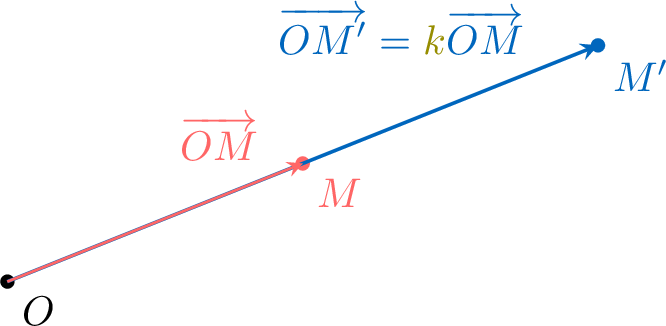
\(\dfrac{\textcolor{colorprop}{OM'}}{\textcolor{colordef}{OM}}=|\textcolor{olive}{k}|\)

\(\dfrac{\textcolor{colorprop}{OM'}}{\textcolor{colordef}{OM}}=|\textcolor{olive}{k}|\)
Example
Find the coordinates of the image of point \(M\) under a homothety with center \(O\) and scale factor \(k=2\).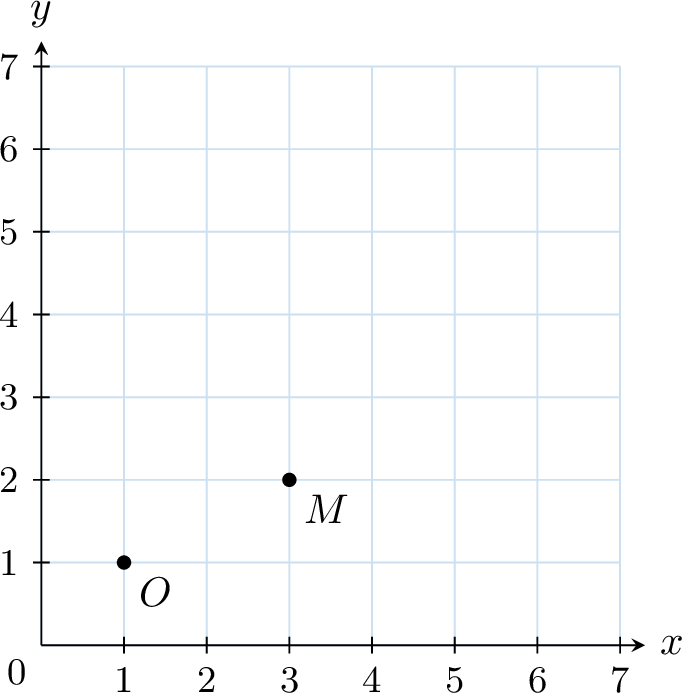

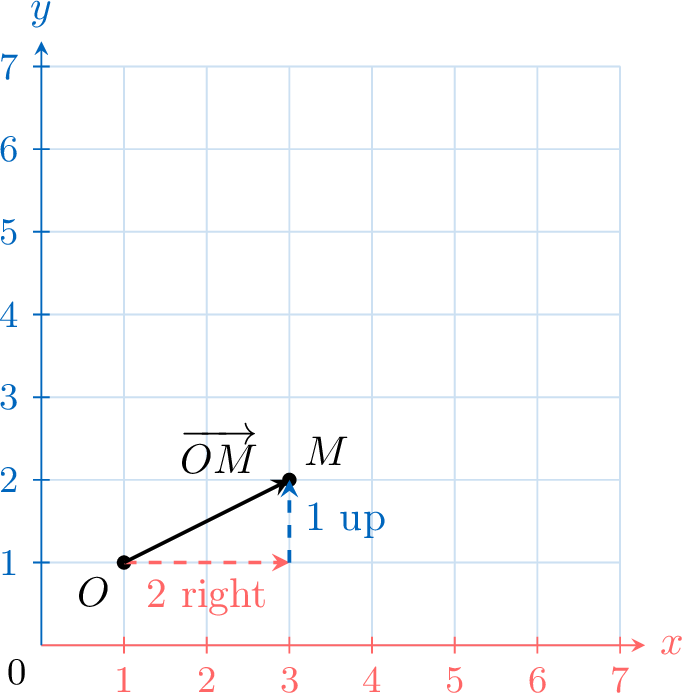
- \(\overrightarrow{OM}\):
- \(\overrightarrow{OM'}=\textcolor{olive}{2}\overrightarrow{OM}\):
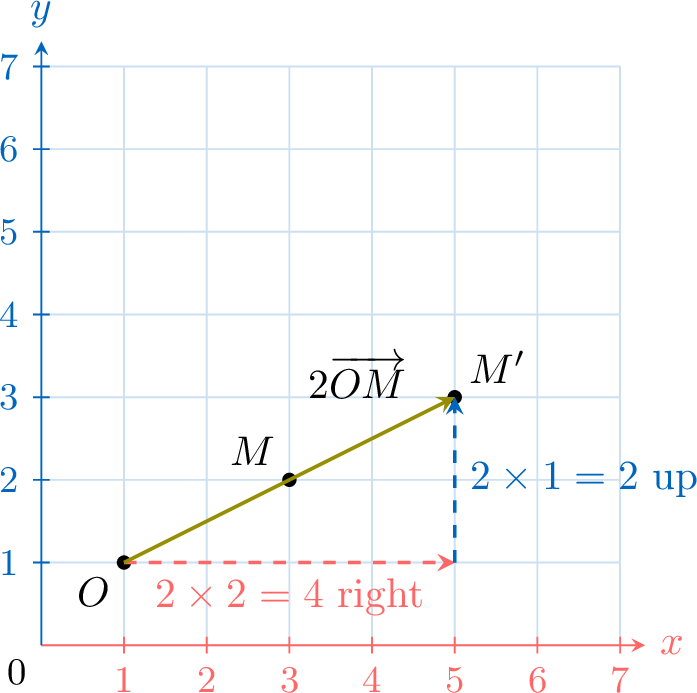
- \(M'(\textcolor{colordef}{5},\textcolor{colorprop}{3})\)
Definition Homothety
The homothety of a figure with center \(O\) and scale factor \(k\) is the homothety of all its points.
Example
The figure \(\textcolor{colorprop}{A'}\) is the image of figure \(\textcolor{colordef}{A}\) under a homothety with center \(O\) and scale factor \(2\).
