Similarity
Definitions
Examine the rectangles shown below. Although their sizes differ, they have the same shape because the proportions of their side lengths are identical.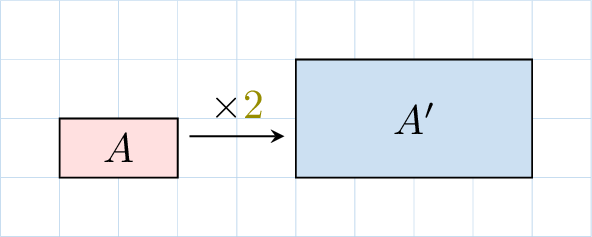

Definition Similarity and Enlargement/Reduction
A similarity is a transformation that multiplies all distances by a scale factor \(k > 0\).
- If \(k \geq 1\), the similarity is an enlargement.

- If \(0 < k < 1\), the similarity is a reduction.
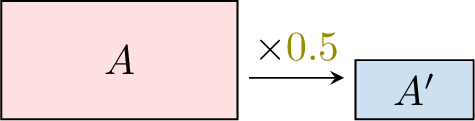
Theorem Fundamental Transformations Similarity Theorem
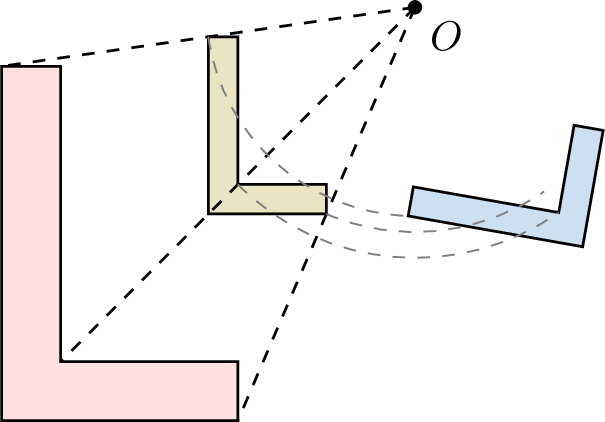
A similarity is the composition of one or more fundamental transformations (reflection, translation, rotation, and homothety).
Example
The blue \(\textcolor{colorprop}{L}\) is similar (by reduction) to the red \(\textcolor{colordef}{L}\).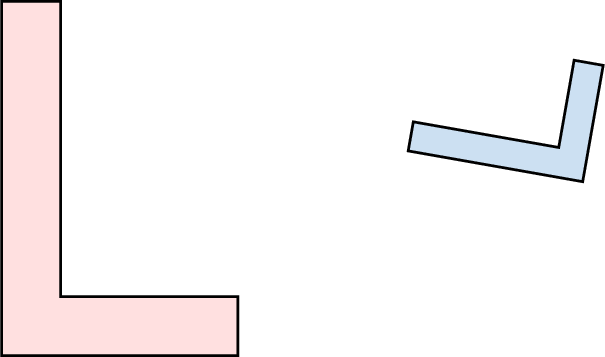


Similar Figures
Definition Similar Figures
Two figures are similar if one is an enlargement or reduction of the other.
The figure \(F'\) is an enlargement of the figure \(F\) by a scale factor of \(2\).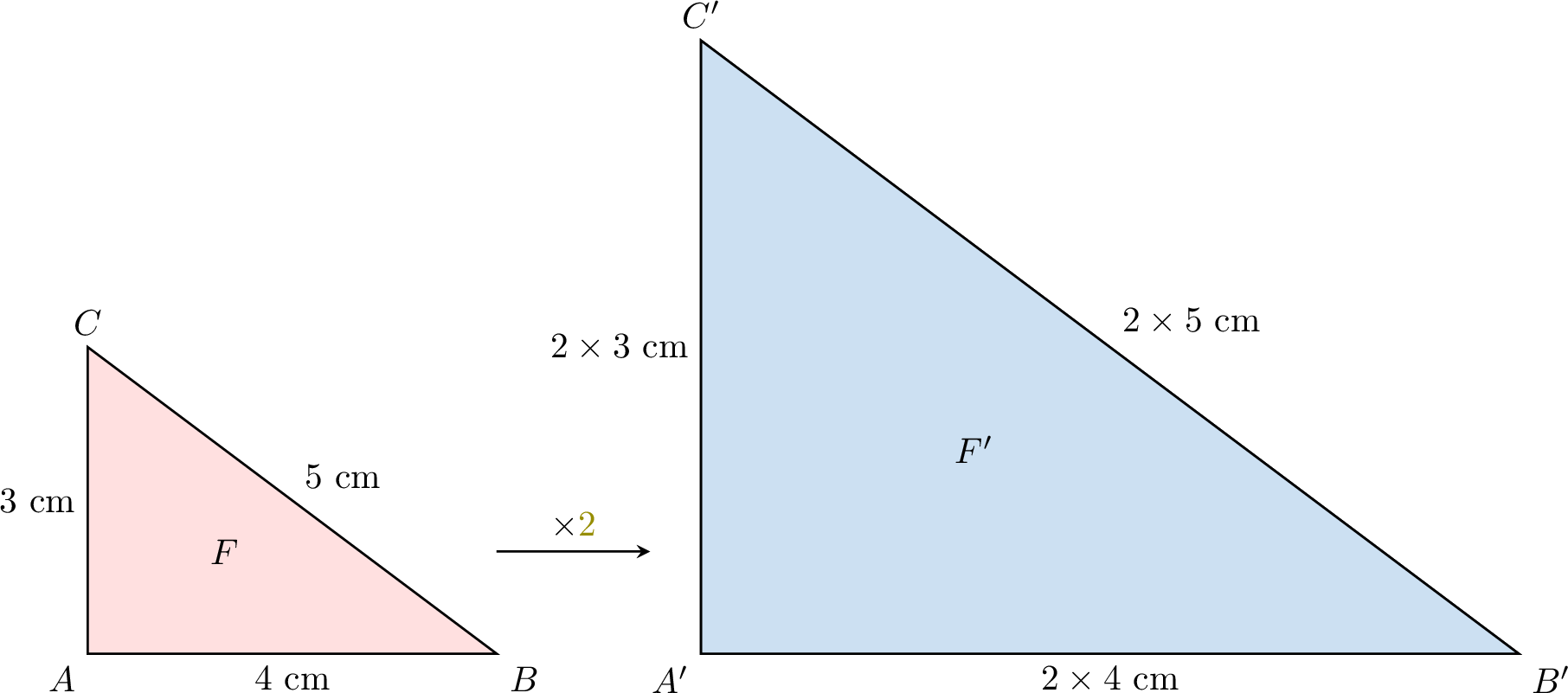

- \(\dfrac{\textcolor{colorprop}{A'B'}}{\textcolor{colordef}{AB}} = \dfrac{2 \times 4~\text{cm}}{4~\text{cm}} = \textcolor{olive}{2}\)
- \(\dfrac{\textcolor{colorprop}{A'C'}}{\textcolor{colordef}{AC}} = \dfrac{2 \times 3~\text{cm}}{3~\text{cm}} = \textcolor{olive}{2}\)
- \(\dfrac{\textcolor{colorprop}{B'C'}}{\textcolor{colordef}{BC}} = \dfrac{2 \times 5~\text{cm}}{5~\text{cm}} = \textcolor{olive}{2}\)
Proposition Properties of Similar Figures
For similar figures:
- The ratios of the corresponding sides are equal to the scale factor.
- The corresponding angles are equal.
Example
The figures \(\textcolor{colordef}{F}\) and \(\textcolor{colorprop}{F'}\) are similar. Find \(x\).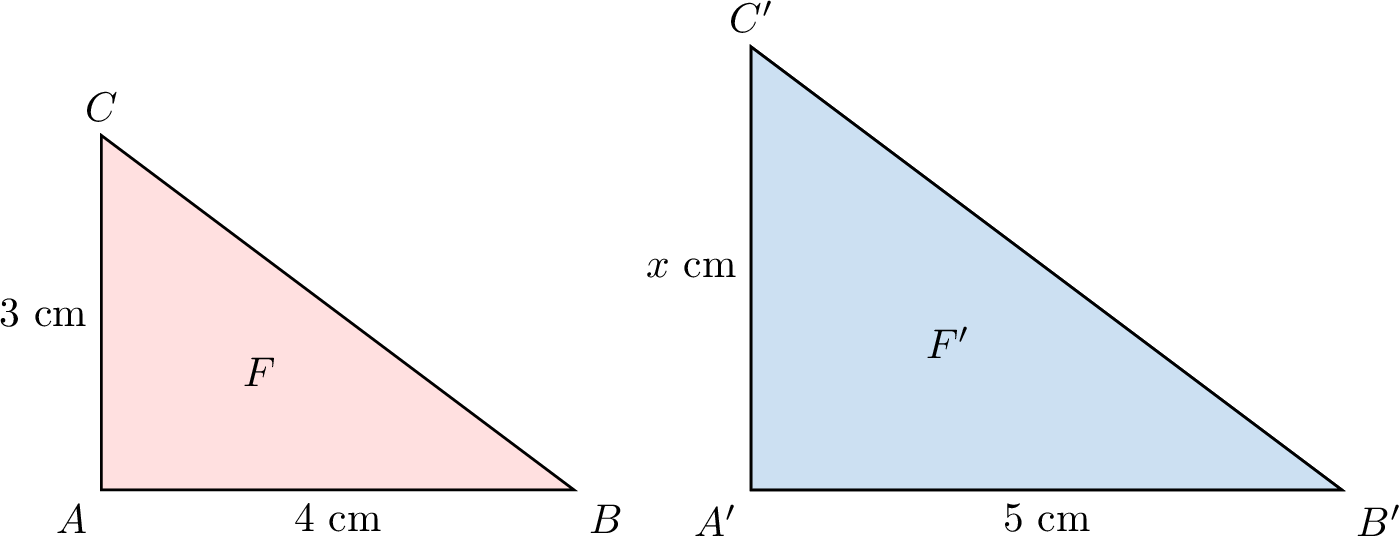

The ratios of the corresponding sides are equal:$$\begin{aligned}\dfrac{\textcolor{colorprop}{A'C'}}{\textcolor{colordef}{AC}} &= \dfrac{\textcolor{colorprop}{A'B'}}{\textcolor{colordef}{AB}} \\\dfrac{x}{3} &= \dfrac{5}{4} \\x &= 3 \times \dfrac{5}{4} \\x &= 3.75\end{aligned}$$