Similar Triangles

Angle-Angle Similarity

Thales, an ancient Greek mathematician, devised a clever method to measure the height of the Great Pyramid of Cheops. One sunny day, he observed that the pyramid cast a shadow 210 meters long. At the same time, a 2-meter-tall broom handle, standing upright, cast a shadow 3 meters long. By comparing these shadows, can you determine the height of the pyramid?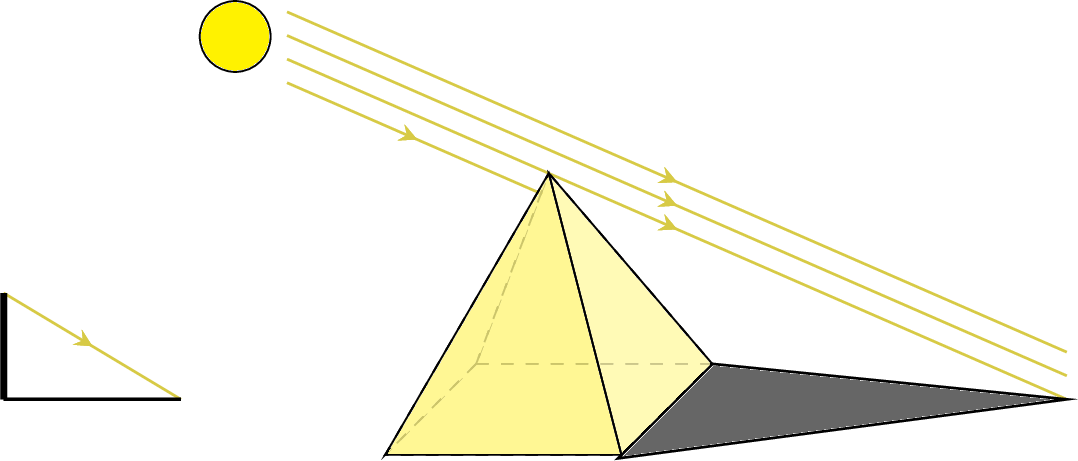

Answer

The triangles formed by the broom handle and its shadow ($T_1: \triangle ABC$) and the pyramid and its shadow ($T_2: \triangle A'B'C'$) are similar.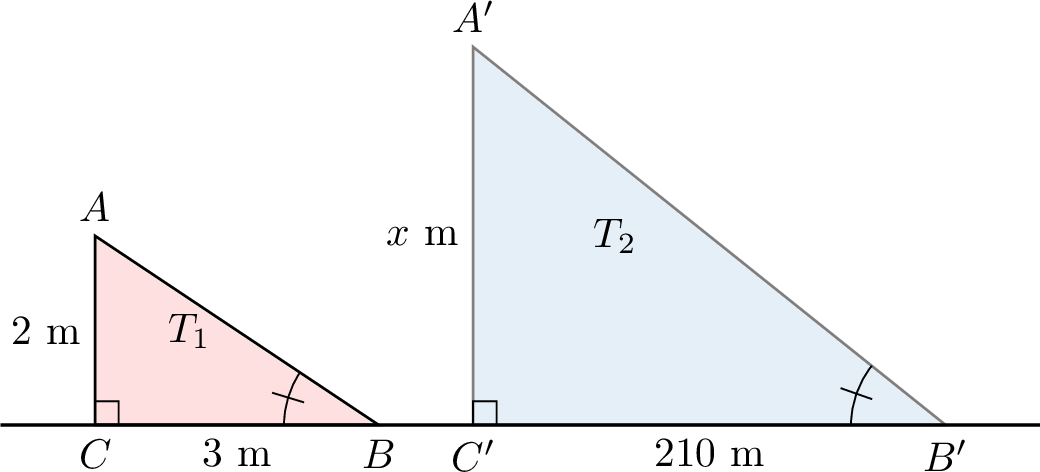

The ratios of corresponding sides are equal:$$\dfrac{\text{height of } T_2}{\text{shadow of } T_2} = \dfrac{\text{height of } T_1}{\text{shadow of } T_1}$$$$\dfrac{x}{210} = \dfrac{2}{3}$$Solving for $x$:$$x = 210 \times \dfrac{2}{3} = \dfrac{420}{3} = 140$$Thus, the height of the Great Pyramid of Cheops is 140 meters.

Proposition Angle-Angle Similarity

If two angles of one triangle are equal to two angles of another triangle, then the two triangles are similar.

Thales’s Theorem

Theorem Thales’s Theorem

Let $\triangle ABC$ be a triangle, with a point $\textcolor{colorprop}{D}$ on the line $\Line{A\textcolor{colordef}{B}}$ and a point $\textcolor{colorprop}{E}$ on the line $\Line{A\textcolor{colordef}{C}}$.
If the line $\textcolor{colorprop}{\Line{DE}}$ is parallel to the line $\textcolor{colordef}{\Line{BC}}$, then the triangles $\textcolor{colordef}{\triangle ABC}$ and $\textcolor{colorprop}{\triangle ADE}$ are similar:$$\dfrac{A\textcolor{colorprop}{D}}{A\textcolor{colordef}{B}} = \dfrac{A\textcolor{colorprop}{E}}{A\textcolor{colordef}{C}} = \dfrac{\textcolor{colorprop}{DE}}{\textcolor{colordef}{BC}}$$Thales’s Configurations: Key Figures

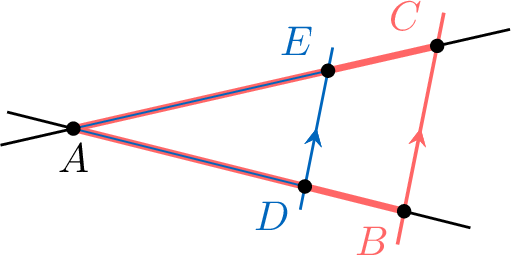
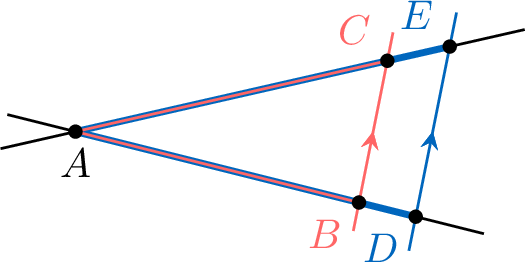
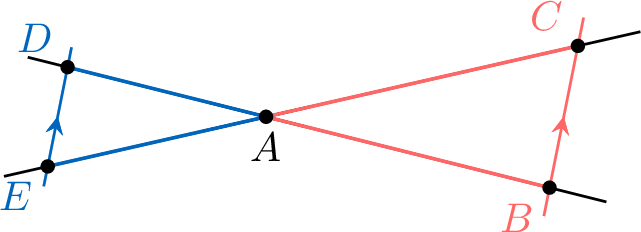
Each red triangle is similar to the blue triangle.

Proof

Since the line $\textcolor{colorprop}{\Line{DE}}$ is parallel to the line $\textcolor{colordef}{\Line{BC}}$, the angles $\angle \textcolor{colorprop}{ADE}$ and $\angle \textcolor{colordef}{ABC}$ are corresponding angles and therefore equal. Additionally, $\angle \textcolor{colorprop}{DAE}$ and $\angle \textcolor{colordef}{BAC}$ are the same angle at vertex $A$. Thus, by the Angle-Angle (AA) similarity criterion, triangles $\textcolor{colordef}{\triangle ABC}$ and $\textcolor{colorprop}{\triangle ADE}$ are similar. Therefore, the ratios of their corresponding sides are equal:$$\dfrac{A\textcolor{colorprop}{D}}{A\textcolor{colordef}{B}} = \dfrac{A\textcolor{colorprop}{E}}{A\textcolor{colordef}{C}} = \dfrac{\textcolor{colorprop}{DE}}{\textcolor{colordef}{BC}}$$