Pythagorean Theorem
One of the oldest and most famous mathematical concepts is the Pythagorean theorem. Named after the ancient Greek mathematician Pythagoras, this theorem establishes a fundamental relationship between the sides of a right-angled triangle.
Right-Angled Triangle
Definition Right-Angled Triangle
A right-angled triangle is a triangle with one right angle. The two sides forming this right angle are called the legs, and the longest side, opposite the right angle, is called the hypotenuse.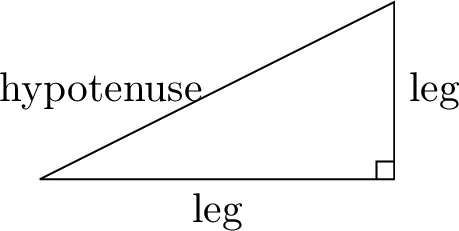

Pythagorean Theorem
- Draw two right-angled triangles, similar to the one shown below:
- Measure the sides of these right-angled triangles to the nearest millimeter and complete the table:
\(\textcolor{colordef}{a}\) \(\textcolor{colorprop}{b}\) \(\textcolor{olive}{c}\) \(a^2\) \(b^2\) \(c^2\) Triangle 1 Triangle 2 - Can you identify any relationship between the values in the columns for \(a^2\), \(b^2\), and \(c^2\)?
- Can you express this relationship as an equation?
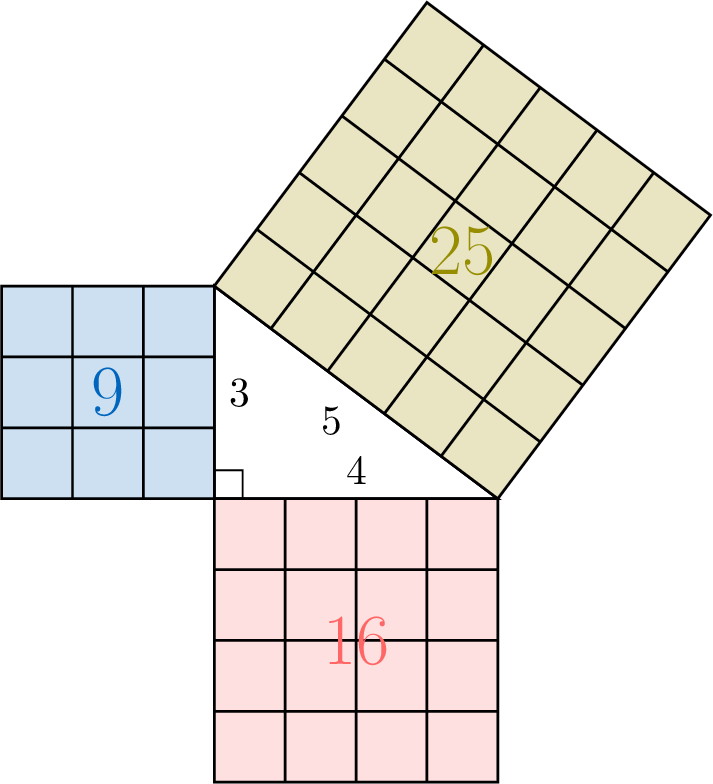
- You have drawn two right-angled triangles. For example:
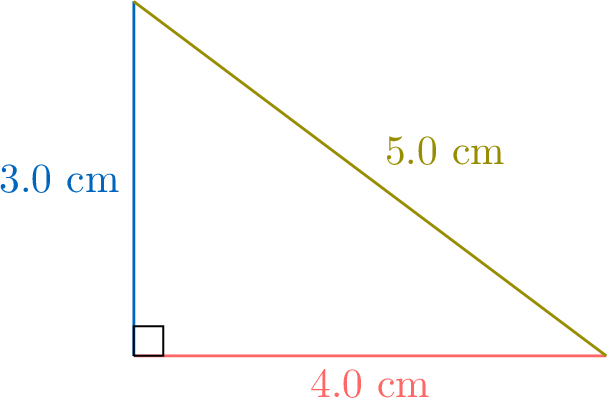
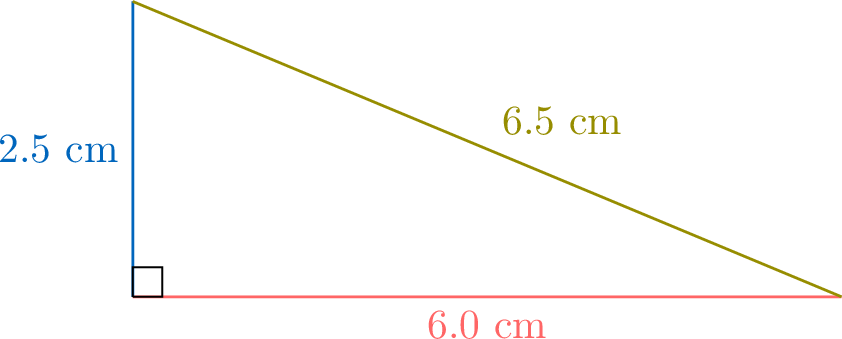
- Here are example measurements of the sides and their squares:
\(\textcolor{colordef}{a}\) \(\textcolor{colorprop}{b}\) \(\textcolor{olive}{c}\) \(a^2\) \(b^2\) \(c^2\) Triangle 1 4 3 5 16 9 25 Triangle 2 6 2.5 6.5 36 6.25 42.25 - From the table, the sum of the squares of the legs (\(a^2 + b^2\)) equals the square of the hypotenuse (\(c^2\)) for both triangles:$$\begin{aligned}16 + 9 &= 25 \\36 + 6.25 &= 42.25\end{aligned}$$
- This relationship is expressed as the equation \(a^2 + b^2 = c^2\), known as the Pythagorean theorem, which states that the sum of the squares of the legs equals the square of the hypotenuse in a right-angled triangle.
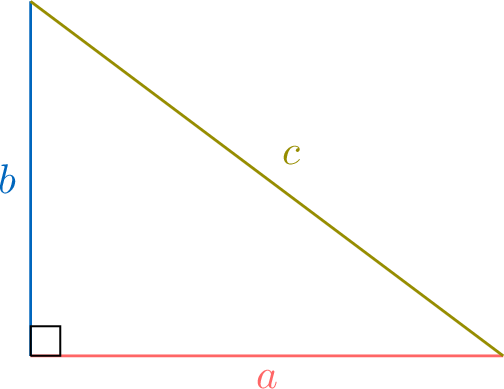
Theorem Pythagorean Theorem
For any right-angled triangle with legs \(a\) and \(b\) and hypotenuse \(c\), the following holds:$$\textcolor{colordef}{a^2} + \textcolor{colorprop}{b^2} = \textcolor{olive}{c^2}$$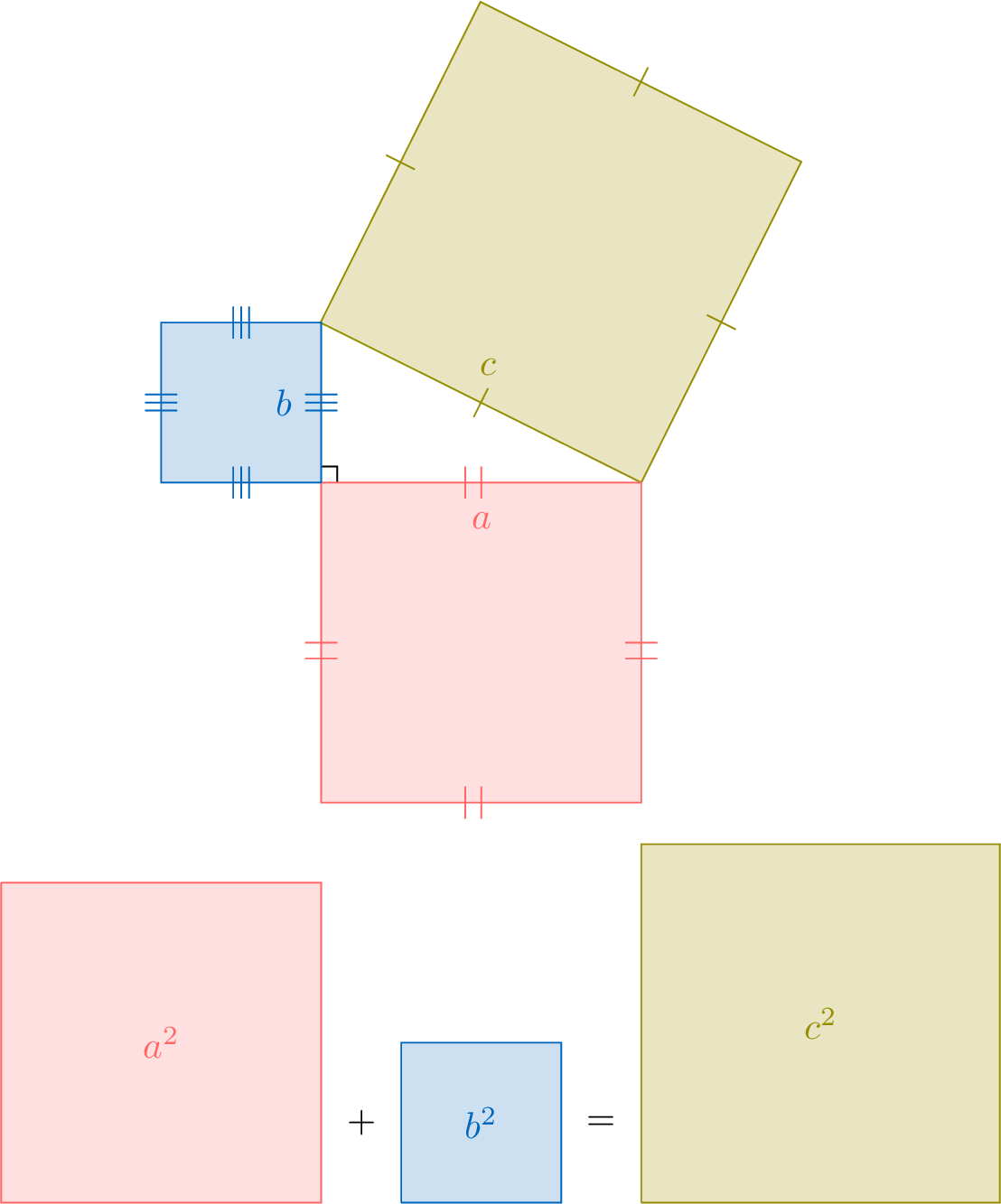

Example
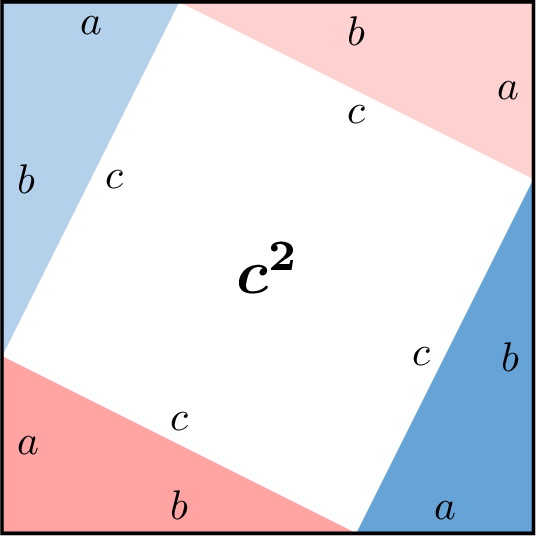
- The geometric proof involves rearranging four identical right-angled triangles within a square of side length \(a+b\).
- In the first arrangement, the four right-angled triangles form a smaller square in the center of the larger square:
- In the second arrangement, the four right-angled triangles form two smaller rectangles within the larger square:
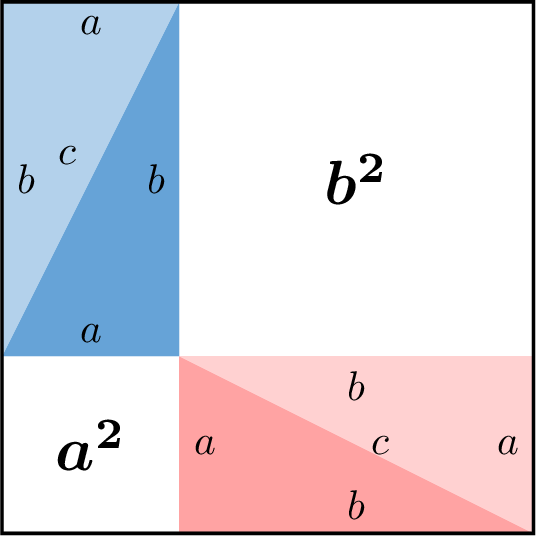
- Since the area not covered by the triangles is equal in both arrangements, we have:$$a^2 + b^2 = c^2$$
- In the first arrangement, the four right-angled triangles form a smaller square in the center of the larger square:
- Algebraic proof: Using four copies of the same triangle arranged symmetrically around a square with side \(c\):
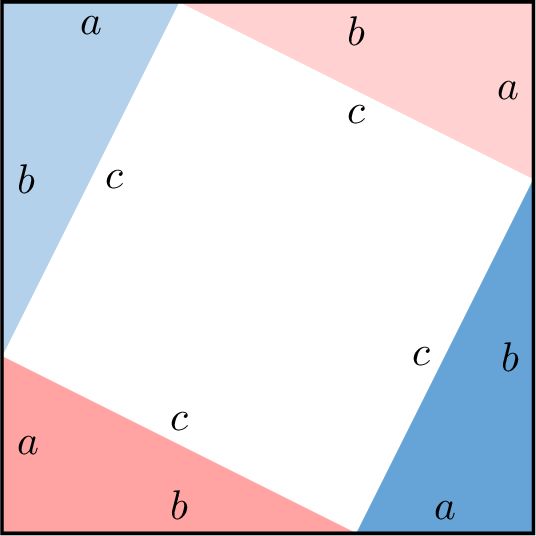
Example
Find the length of the hypotenuse: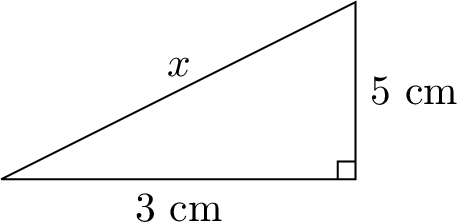

$$\begin{aligned}x^2 &= 3^2 + 5^2 \quad \text{(Pythagorean theorem)} \\x^2 &= 9 + 25 \\x^2 &= 34 \\x &= \sqrt{34} \quad \text{(since the length of a triangle side is positive)}\end{aligned}$$Thus, the hypotenuse has length \(\sqrt{34}\) cm.
Verifying Right-Angled Triangles
Theorem Converse of the Pythagorean Theorem
For any triangle with sides of lengths \(a\), \(b\), and \(c\), if \(a^2 + b^2 = c^2\), then the triangle is right-angled.
Example
Is a triangle with sides of lengths \(3\), \(4\), and \(5\) right-angled?
The two shorter sides are \(3\) and \(4\):$$\begin{aligned}3^2 + 4^2 &= 9 + 16 = 25 \\5^2 &= 25\end{aligned}$$Since \(3^2 + 4^2 = 5^2\), the triangle is right-angled by the converse of the Pythagorean theorem.
Theorem Contrapositive of the Pythagorean Theorem
For any triangle with sides of lengths \(a\), \(b\), and \(c\), where \(c \geq a\) and \(c \geq b\), if \(a^2 + b^2 \neq c^2\), then the triangle is not right-angled.
This is the contrapositive of the Pythagorean theorem.
Example
Is a triangle with sides of lengths \(5\), \(8\), and \(9\) right-angled?
The two shorter sides are \(5\) and \(8\), and the longest side is \(9\):$$\begin{aligned}5^2 + 8^2 &= 25 + 64 = 89 \\9^2 &= 81\end{aligned}$$Since \(5^2 + 8^2 \neq 9^2\), the triangle is not right-angled by the contrapositive of the Pythagorean theorem.