Trigonometry
Trigonometry is a branch of mathematics that explores the relationships between the side lengths and angles of triangles, particularly right-angled triangles. It has wide applications in fields such as science, engineering, astronomy, and video game development. The foundation of trigonometry rests on three primary ratios: sine, cosine, and tangent.
Right-Angled Triangle
Definition Right-Angled Triangle
A right-angled triangle is a triangle with one angle equal to \(90^\circ\). For a given angle \(\theta\) (other than the right angle), we define: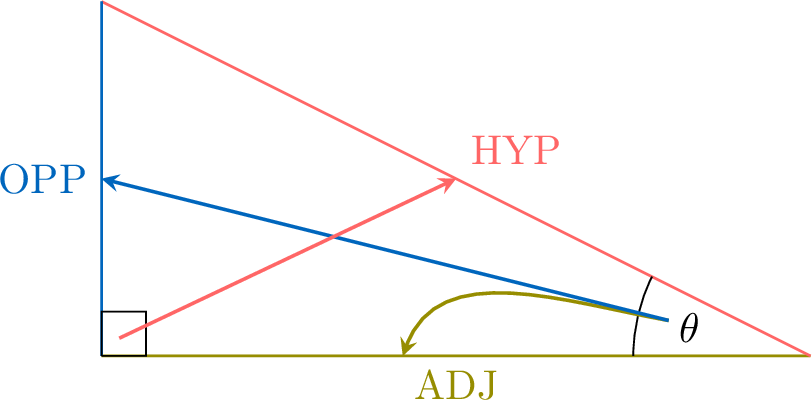
- Hypotenuse (HYP): The longest side, opposite the right angle.
- Adjacent Side (ADJ): The side adjacent to the angle \(\theta\), forming one side of the angle.
- Opposite Side (OPP): The side opposite the angle \(\theta\).

Example
In the triangle below, identify the hypotenuse, the adjacent side, and the opposite side relative to the angle \(\theta\).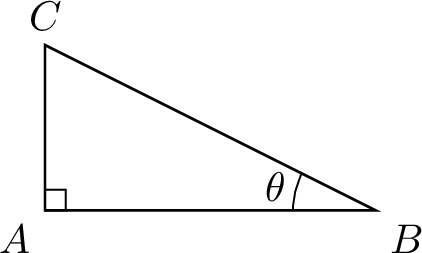

- Hypotenuse: \(\Segment{BC}\)
- Adjacent side: \(\Segment{AC}\)
- Opposite side: \(\Segment{AB}\)
Trigonometric Functions
- Using a protractor and ruler, draw right-angled triangles with angles \(\theta\) of \(15^\circ\), \(30^\circ\), \(45^\circ\), \(60^\circ\), and \(75^\circ\). Measure the lengths of the hypotenuse and the adjacent side to the nearest millimeter.
- Complete the following table with the ratio \(\frac{\text{ADJ}}{\text{HYP}}\) for each angle:
\(\theta\) \(15^\circ\) \(30^\circ\) \(45^\circ\) \(60^\circ\) \(75^\circ\) \(\dfrac{\text{ADJ}}{\text{HYP}}\)
- Examples of right-angled triangles with the specified angles:
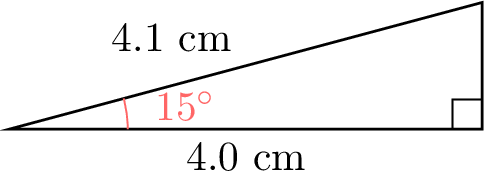
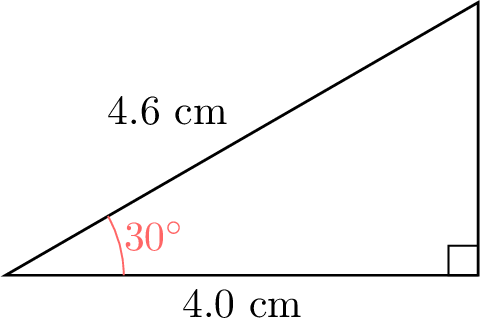
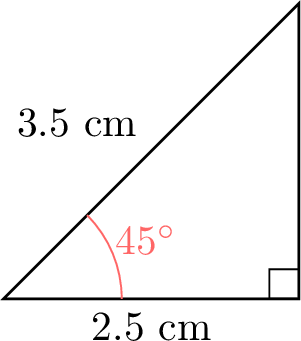
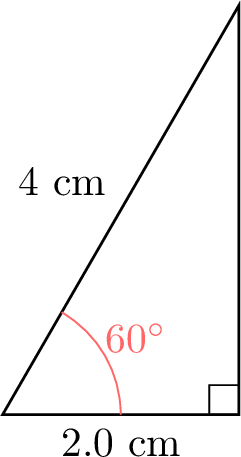
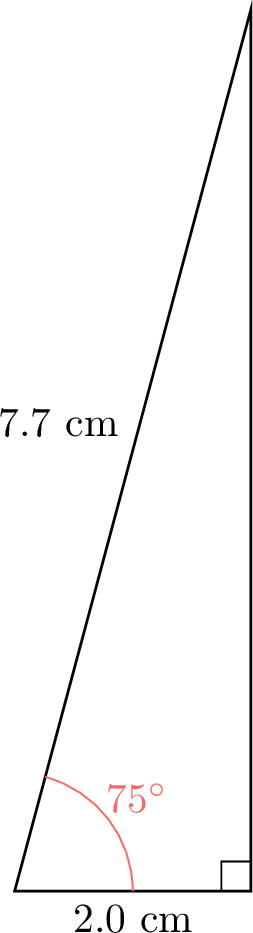
- The ratio \(\dfrac{\text{ADJ}}{\text{HYP}}\) should yield consistent values for each angle, approximately:
\(\theta\) \(15^\circ\) \(30^\circ\) \(45^\circ\) \(60^\circ\) \(75^\circ\) \(\dfrac{\text{ADJ}}{\text{HYP}}\) \(\dfrac{4.0}{4.1} \approx 0.98\) \(\dfrac{4.0}{4.6} \approx 0.87\) \(\dfrac{2.5}{3.5} \approx 0.71\) \(\dfrac{2.0}{4.0} = 0.50\) \(\dfrac{2.0}{7.7} \approx 0.26\)
Proposition Trigonometric Ratios
For any two right-angled triangles with the same angle \(\theta\), the ratios \(\dfrac{\text{OPP}}{\text{HYP}}\), \(\dfrac{\text{ADJ}}{\text{HYP}}\), and \(\dfrac{\text{OPP}}{\text{ADJ}}\) are constant.
Consider two right-angled triangles with the same angle \(\theta\). Since their angles are equal, the triangles are similar. Let \(k\) be the scale factor: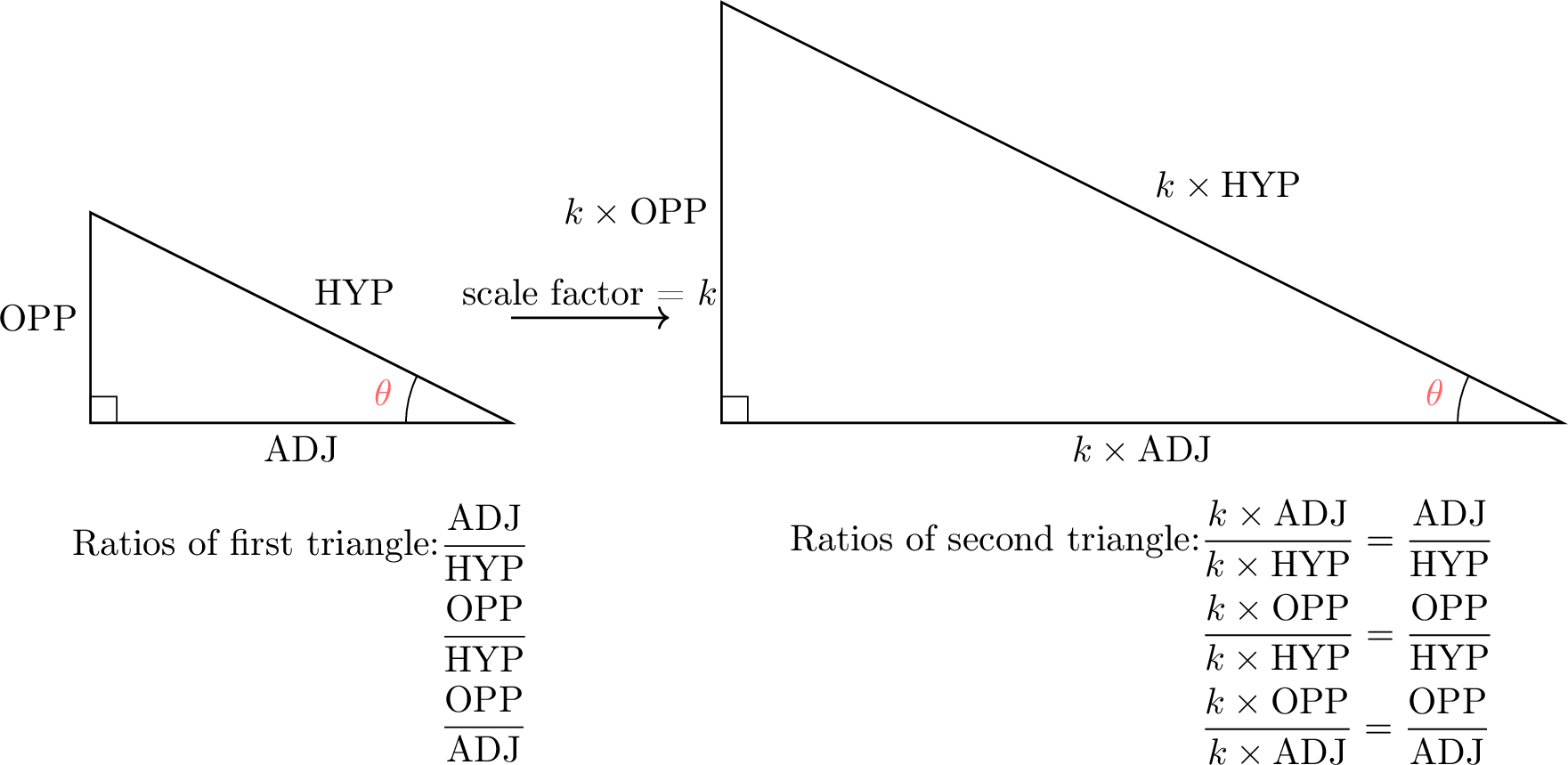

Due to the constant nature of the ratio \(\dfrac{\text{ADJ}}{\text{HYP}}\) for any right-angled triangle with angle \(\theta\), we define the cosine function, denoted \(\cos\), where the input is \(\theta\) and the output is \(\dfrac{\text{ADJ}}{\text{HYP}}\). For example:
| \(\theta\) | \(15^\circ\) | \(30^\circ\) | \(45^\circ\) | \(60^\circ\) | \(75^\circ\) |
| \(\cos(\theta) = \dfrac{\text{ADJ}}{\text{HYP}}\) | \(0.97\) | \(0.87\) | \(0.71\) | \(0.50\) | \(0.26\) |
Definition Trigonometric Functions
In a right-angled triangle with angle \(\theta\):$$\sin(\theta) = \frac{\text{OPP}}{\text{HYP}}, \quad \cos(\theta) = \frac{\text{ADJ}}{\text{HYP}}, \quad \tan(\theta) = \frac{\text{OPP}}{\text{ADJ}}$$
The mnemonic SOH-CAH-TOA helps recall the definitions of sine, cosine, and tangent:
- Sine = Opposite \(\div\) Hypotenuse
- Cosine = Adjacent \(\div\) Hypotenuse
- Tangent = Opposite \(\div\) Adjacent
Example
In the triangle below, find \(\cos \theta\), \(\sin \theta\), and \(\tan \theta\).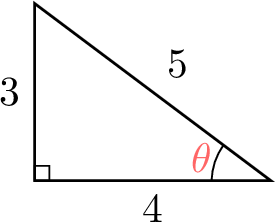

Relative to \(\theta\):
- Hypotenuse: \(BC = 5\)
- Adjacent side: \(AB = 4\)
- Opposite side: \(AC = 3\)
Proposition Tangent Formula
$$\tan \theta = \frac{\sin \theta}{\cos \theta}$$
$$\begin{aligned}\frac{\sin \theta}{\cos \theta} &= \frac{\dfrac{\text{OPP}}{\text{HYP}}}{\dfrac{\text{ADJ}}{\text{HYP}}} \\&= \frac{\text{OPP}}{\text{HYP}} \times \frac{\text{HYP}}{\text{ADJ}} \\&= \frac{\text{OPP}}{\text{ADJ}} \\&= \tan \theta\end{aligned}$$
Method Using Calculator
Trigonometric ratios for any angle can be calculated using a calculator in degree mode. Ensure your calculator is set to "degrees" before performing calculations.
Example
In the triangle below, find \(x\).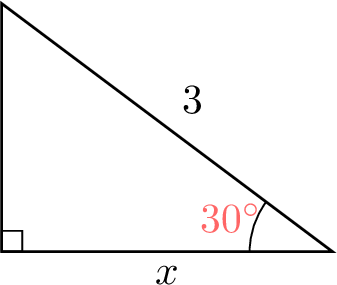

$$\begin{aligned}\cos \theta &= \frac{\text{ADJ}}{\text{HYP}} \\\cos(30^\circ) &= \frac{x}{3} \\x &= 3 \times \cos(30^\circ) \\x &\approx 3 \times 0.866\\x &\approx 2.6 \, \text{cm}\end{aligned}$$
Inverse Trigonometric Functions
Trigonometric ratios can be used to find unknown angles in right-angled triangles when at least two side lengths are known.
Definition Inverse Trigonometric Functions
In a right-angled triangle with angle \(\theta\):$$\theta = \cos^{-1}\left(\frac{\text{ADJ}}{\text{HYP}}\right), \quad \theta = \sin^{-1}\left(\frac{\text{OPP}}{\text{HYP}}\right), \quad \theta = \tan^{-1}\left(\frac{\text{OPP}}{\text{ADJ}}\right)$$
Example
In the triangle below, find \(\theta\).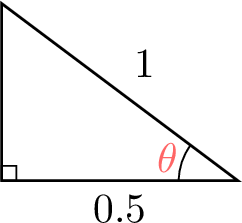

$$\begin{aligned}\theta &= \cos^{-1}\left(\frac{\text{ADJ}}{\text{HYP}}\right) \\&= \cos^{-1}\left(\frac{0.5}{1}\right) \\&= \cos^{-1}(0.5) \\&= 60^\circ\end{aligned}$$